Enoncé

Le théorème, formulé dans une version un peu provoquante affirme que si nous, les humains, avons notre libre arbitre, alors les particules élémentaires ont forcément leur propre part d’un libre arbitre du même type. Plus précisément, si l’expérimentateur peut librement choisir les directions dans lesquelles orienter son appareil pour faire une certaine mesure, alors la réponse de la particule (pour être plus exact, la réponse de l’univers autour de la particule) n’est pas déterminée par toute l’histoire antérieure de l’univers.

Autrement dit, s’il y a un peu de libre arbitre pour les gros systèmes physiques que nous sommes, alors l’Univers est plein de libre arbitre et celui-ci est aussi microscopique. 

Sous une forme plus rigoureuse, le théorème repose sur 3 axiomes nommés SPIN, TWIN, et MIN. Les 2 premiers sont liés à la mécanique quantique, et le dernier est lié à la relativité et à l’idée que l’expérimentateur est libre de ses choix. Il affirme alors :

Les axiomes SPIN, TWIN, et MIN impliquent que la réponse d’une particule de spin 1 à une triple expérience est libre, c’est-à-dire qu’elle n’est pas fonction des propriétés de cette partie de l’univers qui est antérieure à cette réponse et cela par rapport à n’importe quel référentiel inertiel.

Histoire du théorème

« Le théorème du libre arbitre » est le résultat de l’association de 2 mathématiciens John H. Conway et Simon B. Kochen, ce dernier étant aussi spécialistes de mécanique quantique. Une première version a été présentée dans un article publié dans Foundations of Physics en 2006. Une version dite renforcée a été ensuite produite en 2009. Renforcée dans le sens où l’un des 3 axiomes nécessaires à la démonstration a été remplacé par un axiome plus faible (c’est-à-dire moins exigeant). Concrètement l’axiome FIN avec l’hypothèse du libre choix des expérimentateurs et de la causalité temporelle (ce qui paraissait déjà raisonnable) a été remplacé par l’axiome MIN qui permet aux réactions des particules de dépendre des demi-espaces passés plutôt que seulement des cônes de lumière passés (c’est-à-dire que la vitesse de la lumière n’est plus supposée limitée, elle pourrait être infinie).

Il est l’aboutissement d’une série de théorèmes apparus depuis le début des années 1960 sur la mécanique quantique avec en particulier le théorème de Bell en 1964, et le paradoxe Kochen-Specker en 1967 qui est un élément central de la démonstration.

Le principe de la démonstration

La démonstration présentée ici suit scrupuleusement l’article publié par les auteurs John Conway et Simon Kochen en 2009 pour le théorème dans sa version forte. 

Le théorème se base sur l’idée que deux expérimentateurs humains nommés A et B séparés par une certaine distance vont procéder à des mesures sur des particules atomiques, a et b, et utiliser leur libre-arbitre pour choisir, au dernier moment, quelle mesure ils vont faire.  Plus précisément, ils vont effectuer chacun des mesures de spin sur une particule élémentaire, à savoir l’expérimentateur A sur la particule a et l’expérimentateur B sur la particule b, mais ces deux particules seront « intriquées ». Les deux expérimentateurs vont faire ces mesures quasi simultanément, de telle sorte que chaque expérimentateur n’a pas la possibilité de transmettre l’information « je vais faire la mesure suivant cet axe » à l’autre avant que ce dernier n’ait enregistré le résultat de sa mesure.

Le théorème repose sur trois axiomes nommés « Spin », « Twin », et « Min ».

1. « Spin » : le carré des composantes de spin de certaines particules de spin 1, mesuré dans trois directions orthogonales, est toujours une permutation de (1,1,0). 
2. « Twin » : Il est possible « d’intriquer » deux particules élémentaires et de les séparer spatialement ensuite, de telle manière que si on mesure ensuite leur spin selon deux directions identiques (c’est-à-dire parallèles), les carrés de la composante de spin suivant cette direction seront identiques pour les 2 particules.  
3. « Min » : cet axiome combine principe de causalité temporelle et principe de libre arbitre des expérimentateurs. Pour ce qui est du principe de causalité temporelle, il fait l’hypothèse que l’avenir ne peut pas modifier le passé. Exprimé sous sa forme relativiste cela signifie qu’un événement ne peut pas être influencé par ce qui se passe plus tard dans un référentiel inertiel donné quel qu’il soit. Une autre hypothèse, généralement tacitement utilisée, est que les expérimentateurs sont libres de choisir entre les expériences possibles. Cela conduit à pouvoir dire que le choix d’un expérimentateur n’est pas fonction du passé. L’axiome MIN repose sur quelques cas très particuliers de ces hypothèses.

Ces trois axiomes sont parfaitement « raisonnables » au sens où les physiciens quantiques les considèrent comme vrais tous les trois. En particulier si « Spin » ou « Twin » étaient faux les fondements même de la mécanique quantique seraient ébranlés. Ilssont utilisés dans une expérience de pensée au cours de laquelle les expérimentateurs A et B font des mesures de spin suivant des directions qui sont choisies parmi un ensemble particulier de directions, à savoir la configuration de Peres : elle comprend 33 axes d’orientation différentes et est associée à 40 trièdres orthogonaux. 

La démonstration du théorème proprement dit et courte et découle très directement de l’application des 3 axiomes mis en œuvre avec la configuration de Peres. Cette configuration n’est pas compatible avec une certaine propriété, dite 101, or si l’on admet les conséquences logiques des 3 axiomes alors nous devons admettre le libre arbitre de la paire de particule intriquée a, b (libre arbitre au sens de Conway/Kochen) car sinon la configuration de Peres aurait la propriété 101.

La configuration de Peres et ses propriétés sont un passage obligé pour appréhender ensuite la démonstration, et sont longuement présentées dans le paragraphe Boîte à outils.

Boîte à outils

1) Définition du libre arbitre au sens de Conway/Kochen :

Dire que le choix de x, y, z de A est libre signifie pour les auteurs qu’il n’est pas déterminé par (c’est à dire n’est pas une fonction de) ce qui s’est passé auparavant (dans n’importe quel référentiel inertiel). Le théorème établit la conséquence surprenante que la réponse d’une particule doit être libre dans exactement le même sens, que cette réponse n’est pas une fonction de ce qui s’est passé plus tôt (par rapport à n’importe quel référentiel inertiel).

Ce libre arbitre, qui n’a rien à voir avec les notions de probabilités puisqu’il affirme juste la non-existence d’une certaine fonction. Il s’agit d’un indéterminisme logique (ou si l’on veut préciser, fonctionnel). Cet indéterminisme est l’impossibilité́ logique qu’il existe certaines fonctions reliant les états de l’Univers, impossibilité́ qui signifie que d’instant en instant l’Univers n’est pas contraint par son passé, mais libre de son évolution. 

2) La configuration de Peres et la propriété 101 :

Considérons un cube de centre C et les 3 axes x, y, z parallèles aux arrêtes du cube.

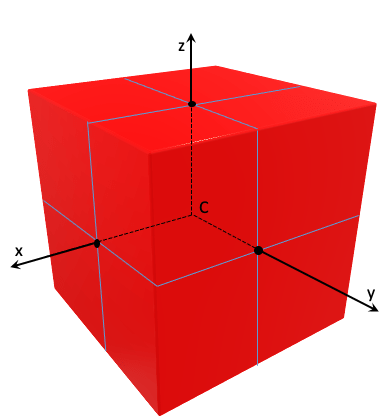
Figure 1

Les axes x, y et z sont 3 axes de symétrie de ce cube. Les points d’intersection de ces axes avec le cube sont indiqués en noir. Le cube a 10 autres axes de symétrie, donnés par les directions en bleu de la figure suivante. Les intersections de ces axes de symétrie avec le cube sont données par les points en bleu.

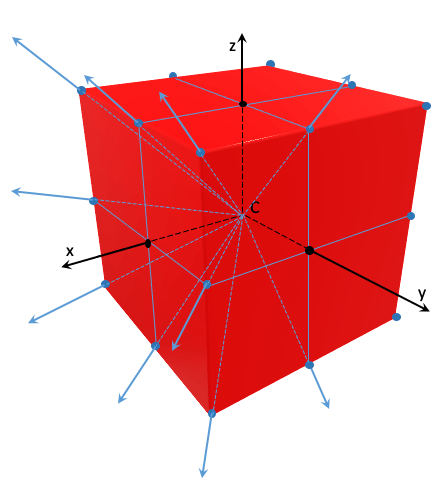
Figure 2

Ces 13 axes définissent 13 directions, numérotées de 1 à 13 dans la figure 3 qui associe à chaque axe le point d’intersection avec le cube, et le numéro d’axe correspondant. Parmi ces axes, plusieurs triplets forment un repère orthogonal : par exemple (8,9,3), (1,13,7), (11,2,5), …

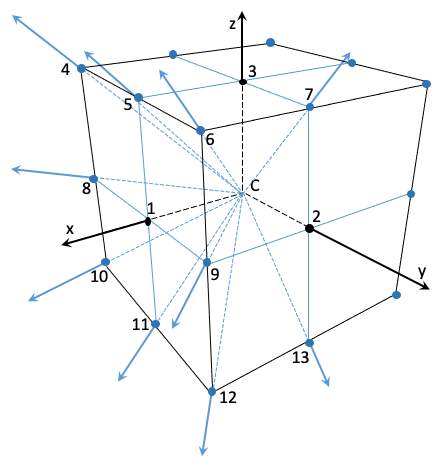
Figure 3

Faisons maintenant tourner de 45° autour de z l’ensemble de ces 13 axes (figure 4).

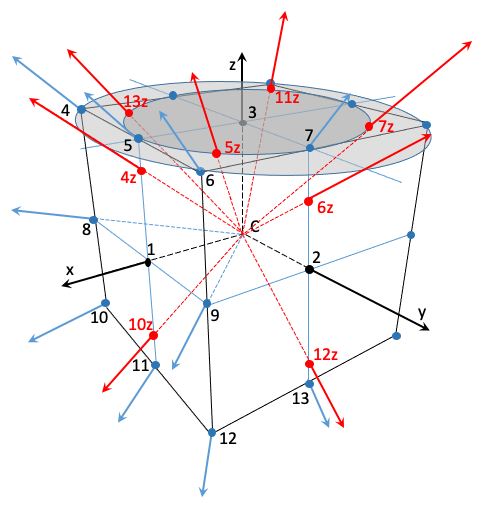
Figure 4

Suite à cette rotation :

• L’axe 3 reste sur 3,
• L’axe 1 devient 9, 9 devient 2, 2 devient 8, et 8 devient 1,
• L’axe 4 se retrouve dans le plan (x,z) et coupe le cube initial en un nouveau point 4z,
• L’axe 5 se retrouve sur le plan formé par z et la diagonale des axes x et y. Il coupe le cube en un nouveau point 5z.

De même les axes 6, 7 10, 11, 12, 13 se retrouvent sur des directions nouvelles par rapport aux 13 directions de départ, et intersectent le cube en des nouveaux points 6z, 7z, 10z, 11z, 12z, 13z.

Par cette opération nous avons construit les axes 3, 9, 2, 8, 1 ainsi que 8 axes supplémentaires, identifiés par les points 4z, 5z, 6z, 7z, 10z, 11z, 12z, 13z. Nous disposons des axes construits suivants : 1, 2, 3, 8, 9, 4z, 5z, 6z, 7z, 10z, 11z, 12z, 13z.

Effectuons une rotation de 45° autour de l’axe x pour les 13 axes de départ (figure 5).

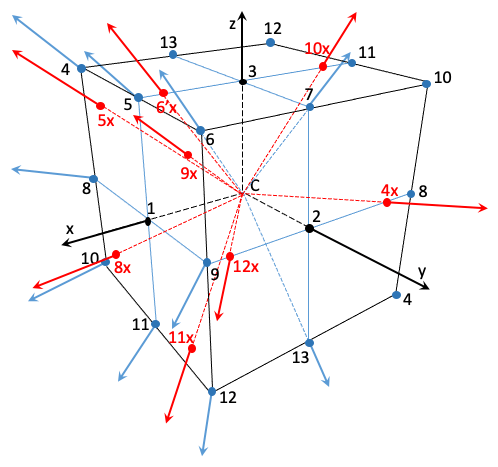
Figure 5

Suite à cette rotation :

• L’axe 1 reste sur 1,
• L’axe 2 devient 7, 7 devient 3, 3 devient 13, et 13 devient 2,
• L’axe 4 se retrouve dans le plan (x,y) en diagonale des directions  x et y, et coupe le cube initial en un nouveau point 4x,
• L’axe 5 se retrouve en 5x.

De même les axes 6, 8, 9, 10, 11, 12 se retrouvent sur des directions nouvelles par rapport aux 13 directions de départ, et intersectent le cube en des nouveaux points 6x, 8x, 9x, 10x, 11x, 12x.

Nous avons ainsi construit les axes 1, 7, 3, 13, 2, 4x, 5x, 6x, 8x, 9x, 10x, 11x, 12x. Les axes construits par les rotations z plus ceux construits par les rotations x sont au nombre de 23, il s’agit de :

1, 2, 3, 7, 8, 9, 13, 4z, 5z, 6z, 7z, 10z, 11z, 12z, 13z, 4x, 5x, 6x, 8x, 9x, 10x, 11x, 12x.

Effectuons maintenant une rotation de 45° autour de l’axe y pour les 13 axes de départ (figure 6).

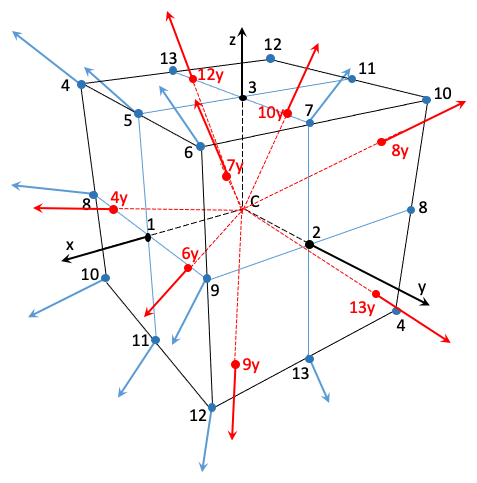
Figure 6

Suite à cette rotation :

• L’axe 2 reste sur 2,
• L’axe 1 devient 11, le 11 devient 3, le 3 devient 5, et le 5 devient 1.

Nous faisons apparaître cette fois les nouveaux axes 4y, 6y, 7y, 8y, 9y, 10y, 12y, et 13y.

Par cette rotation nous avons ainsi construit les axes : 2, 11, 3, 5, 1, 4y, 6y, 7y, 8y, 9y, 10y, 12y, et 13y.

Le total des axes images des 13 axes initiaux, par les rotations autour de z, par les rotations autour de x, et par les rotations autour de y sont au nombre de 33, il s’agit de : 

1, 2, 3, 5, 7, 8, 9, 11, 13, 4z, 5z, 6z, 7z, 10z, 11z, 12z, 13z, 4x, 5x, 6x, 8x, 9x, 10x, 11x, 12x, 4y, 6y, 7y, 8y, 9y, 10y, 12y, et 13y. 

Ces 33 axes sont les axes de symétrie de la figure géométrique constituée par la superposition des cubes bleu, rouge et vert tels que présentés dans la figure 7 et qui sont chacun les images du cube initial par rotation de 45° autour de z (cube bleu), de 45° autour de x (cube rouge) et de 45° autour de y (cube vert).

Figure 7

La figure 8 représente les 33 points d’intersection des 33 axes avec le cube initial. La direction de chacun des axes est donnée par la droite passant par le centre du cube et le point d’intersection (nous confondons le nom du point et le nom de l’axe). Ces 33 axes constituent ce que l’on appelle la configuration de Peres.

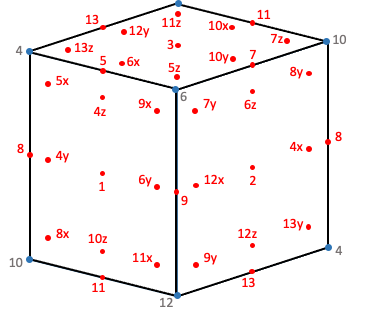
Figure 8

La configuration de Peres contient 16 triplets orthogonaux, à savoir :

(1,2,3), (9, 8, 3), (2, 5, 11), (1, 7, 13), (8, 5z, 11z), (9, 7z, 13z), (9x, 8x, 3), 

(7 ,5x, 11x), (9y, 8y, 5), (11, 7y, 13y), (3, 4y, 12x), (3, 6y, 4x), (2, 6x, 10z), 

(2, 4z, 10x), (1, 6z, 12y), (1, 12z, 10y).

Ces trièdres sont chacun construits à partir de 3 axes orthogonaux appartenant à la configuration. Nous notons E₁₆ cet ensemble de trièdres. Nous allons maintenant nous intéresser à un ensemble de trièdres plus large, qui est l’ensemble des trièdres qui peuvent être construits à partir d’au moins 2 axes orthogonaux appartenant à la configuration de Peres. Cet ensemble contient déjà les 16 triplets orthogonaux de E₁₆. Il doit aussi contenir tous les trièdres qui ont 1 axe orthogonal à seulement une paire d’axes orthogonaux qui appartiennent la configuration de Peres. 

Cela signifie par exemple que :

• Il doit contenir le trièdre formé à partir des axes 5x et 9y auxquels on ajoute l’orthogonal au plan 5x, 9y
• Il doit contenir le trièdre formé à partir des axes 8x et 7y auxquels on ajoute l’orthogonal au plan 8x, 7y
• Idem pour les trièdres qui seront construits à partir de 11x, 8y ou 9x, 13y etc…

Nous trouvons dans la configuration de Peres 24 paires d’axes dont l’axe orthogonal à la paire en question ne fait pas déjà partie de la configuration. Ces paires sont facilement identifiables en prenant d’abord le plan contenant l’axe 3 et les 3 points 5x, 4y, et 8x, ainsi que le plan contenant l’axe 3 et les 3 points 7y, 12x et 9y. Comme ces 2 plan sont orthogonaux, chaque paire de points constituées d’un point du premier plan et d’un point du second plan donne une paire d’axes orthogonaux. Cela donne 9 paires, dont une, la paire 4y, 12x doit être éliminée car le trièdre 4y, 12x, 3 est dans E₁₆. Nous obtenons ainsi 8 paires dont l’axe orthogonal à la paire en question n’est pas dans la configuration de Pères (on ne trouve pas ces paires dans l’un des 16 trièdres de E₁₆). Les mêmes opérations répétées en utilisant les plans contenant l’axe 2 puis les plans contenant l’axe 1 donneront chacune 8 paires.

Chacune de ces paires permet de construire un trièdre qui n’est pas dans E₁₆. Ces 24 trièdres sont forcément tous différents, en effet si 2 paires différentes conduisaient à construire le même axe orthogonal, cela signifierait que ces paires d’axes sont dans le même plan, et on peut vérifier que cela n’est pas le cas. Ajoutés aux 16 trièdres précédents, ces 24 nouveaux trièdres permettent de constituer un ensemble de 40 trièdres, que nous nommerons E₄₀.

Convenons maintenant d’assigner à chaque axe d’un trièdre quelconque une valeur 0 ou 1. Pour tout trièdre nous dirons qu’il possède la propriété 101 si 2 des 3 axes du trièdre ont la valeur 1 et le troisième la valeur 0. Autrement dit, on ne trouve jamais 2 fois la valeur 0 pour toute paire d’axes orthogonaux de ce trièdre.

Théorème d’incompatibilité : il est impossible de distribuer des valeurs 1 ou 0 sur les 33 axes de la configuration de Peres d’une façon telle que tous les éléments de E₄₀ aient la propriété 101.

Démonstration de l’incompatibilité :

Partons du triplet (1, 2, 3) et supposons qu’il ait la propriété 101, c’est-à-dire, sans perte de généralité, que les axes 1 et 3 prennent la valeur 1, et l’axe 2 la valeur 0.

Axe 2 à 0 implique que les axes 5 et 11 ont tous les 2 pour valeur 1.

L’axe 11, avec sa valeur 1, forme un trièdre avec les axes 7y et 9y (cf figure 6) donc : l’un de ces 2 axes 7y et 9y prend pour valeur 0 et l’autre 1. (1)

De la même façon 5 forme un trièdre avec 8y et 13y et l’un des 2 axes prend pour valeur 0 donc : l’un des 2 axes 8y et 13y prend pour valeur 0 et l’autre 1.  (2)

Par rotation de 90° autour de 3, les axes 5x, 4y, 8x se retrouvent en 7y, 12x, 9y, ce qui montre que 4y est orthogonal à 7y et à 9y (le plan 5x, 4y, 8x passant par C et le plan 7y, 12x, 9y passant par C sont orthogonaux). 

• cas où 7y = 0 et 9y = 1 :  4y prend la valeur1 car 4y et 7y étant orthogonaux, ils ne peuvent pas être simultanément à 0 (cf lemme).
• Cas ou 7y = 1 et 9y = 0 : 4y prend la valeur1 car 4y et 9y étant orthogonaux, ils ne peuvent pas être simultanément à 0.

Dans les 2 cas : 4y vaut 1.

Comme 3 et 4y valent 1 on en déduit que 12x vaut 0 par le triplet 3, 4y, 12x. 8x et 5x sont orthogonaux à 12x qui vaut 0, donc 8x et 5x ont pour valeur 1.

Raisonnons maintenant de la même façon pour les axes 9x, 6y, 11x qui, après rotation de 90° autour de 3 se retrouvent en 8y, 4x, 13y. Cette fois 6y est orthogonal à 8y et 13y qui valent (cf (2) ) 0 et 1 ou 1 et 0, donc 6y vaut 1. Le triplet 3, 6y, 4x est un triplet orthogonal, donc 4x vaut 0. 9x et 11x sont orthogonaux à 4x, ils sont donc tous les deux à 1.

Or, les axes 9x, 8x, 13 forment un triplet orthogonal, qui est l’image de 5, 11, 2 par la rotation de 45° autour de x. De même 5x, 11x, 7 est un triplet orthogonal image de 5, 11, 2 par la rotation -45° autour de x. On en déduit que 13 vaut 0, et que 7 vaut 0, donc le triplet 1, 7, 13 qui est orthogonal n’a pas la propriété 101. CQFD

Nota : il est impossible d’affecter des 0 ou 1 aux 33 axes de la configuration de Peres tout en ayant la propriété 101 pour les 40 trièdres de E₄₀, en revanche il est possible d’affecter des 0 ou 1 aux 33 axes de la configuration tout en ayant la propriété 101 si l’on se limite aux 16 trièdres de E₁₆.

Démonstration du théorème du libre arbitre

Quelques précisions sur les termes. Les mots « propriétés », « événements » et « information » sont utilisés presque de façon interchangeable, ‘un événement s’est produit ‘ est considéré comme une propriété et ‘une propriété est obtenue’ peut être codé par un bit d’information. Le sens général exact de ces termes, qui peut être différents dans certaines théories qui considèrent ces concepts, n’est pas important, car ils ne sont ici employés que dans le contexte spécifique des trois axiomes.

Pour ce qui est du sens à donner à la notion de libre arbitre, il faut se référer au paragraphe 1 de la Boîte à outil qui traite cette question.

Commençons par énoncer les 3 axiomes :

• Axiome SPIN :

L’axiome implique l’opération appelée « mesure du spin carré d’une particule de spin 1 », qui produit toujours le résultat 0 ou 1. Un noyau d’hélium est par exemple une particule de spin 1.

Énoncé de l’axiome SPIN : Pour une particule de spin 1, la mesure des carrés des composants du spin suivants 3 directions orthogonales donnent toujours les réponses 1, 0, 1 dans un certain ordre. 

La mécanique quantique prédit cet axiome puisqu’elle dit que pour une particule de spin 1 les composantes S_x, S_y S_z du spin suivants les axes x, y, et z vérifient: S_x²+S_y²+S_z² = 2 avec x, y, z interchangeables, quel que soit le repère orthogonal de mesure.

Cette « propriété 101» est paradoxale puisque l’on vient de voir qu’elle ne peut mathématiquement pas être respectée suivant toutes les directions possibles alors que la mécanique quantique affirme elle que la relation S_x²+S_y²+S_z² = 2 est vraie quelle que soit la direction. Malgré ce paradoxe aucun physicien ne remettrait en question la vérité de l’axiome SPIN, car il découle de la mécanique quantique, qui est l’une des théories scientifiques les plus fortement étayées de tous les temps. La notion de libre arbitre telle qu’utilisée dans le théorème donne la clé pour surmonter la contradiction.

• Axiome TWIN

Un des faits les plus curieux de la mécanique quantique a été mis en évidence par Einstein, Podolsky, et Rosen en 1935. Il établit que bien que les résultats de certaines observations distantes ne peuvent pas être prédits individuellement à l’avance, ils peuvent être corrélés.

En particulier, il est possible de produire une paire de particules de spin 1 « jumelées » ou dites intriquées (en les plaçant dans un état de spin total nul) qui donnera pour des directions parallèles les mêmes réponses aux mesures de spin carré ci-dessus. L’axiome « TWIN » est inclus dans cette assertion.

Énoncé de l’axiome TWIN : Soit des particules jumelées de spin 1, et 2 expérimentateurs A et B. Supposons que l’expérimentateur A effectue une triple expérience de mesure sur le carré de la composante du spin de la particule a selon trois directions orthogonales x, y, z, tandis que l’expérimentateur B mesure la particule jumelée b dans une direction, w. Si w se trouve dans la même direction que l’une des mesures de x, y, z, alors l’expérimentateur B donnera nécessairement la même réponse que la mesure correspondante faite par l’expérimentateur A.

En fait, nous allons restreindre w, la direction choisie par l’expérimentateur B, à l’une des 33 directions de la configuration de Pères, et x, y, z, le triplet choisi par l’expérimentateur A, à l’un des 40 triplets orthogonaux de l’ensemble E₄₀.

• Axiome MIN :

L’un des paradoxes introduits par la théorie de la relativité fut le fait que l’ordre temporel dépend du choix du référentiel inertiel dans lequel les mesures sont faites. Si deux événements sont espacés, alors ils apparaîtront dans un ordre temporel dans certains référentiels inertiels, mais dans l’ordre inverse dans d’autres. Les deux événements que nous considérerons seront les mesures de spin jumelées telles que définies précédemment.

Il est habituel de supposer tacitement le principe de causalité temporelle qui est que l’avenir ne peut pas modifier le passé. Sa forme relativiste est qu’un événement ne peut pas être influencé par ce qui se passe plus tard dans un référentiel inertiel donné quel qu’il soit. Une autre hypothèse généralement tacite est que les expérimentateurs sont libres de choisir entre les expériences possibles. Dans cet article, libre choix s’entend au sens que le choix d’un expérimentateur n’est pas fonction du passé. L’axiome MIN n’utilise explicitement que quelques cas très particuliers de ces hypothèses.

Énoncé de l’axiome MIN : Supposons que les expériences effectuées par A et B sont séparées dans l’espace. Alors l’expérimentateur B peut librement choisir n’importe laquelle des 33 directions particulières w, et la réponse de la particule a est indépendante de ce choix. De même et indépendamment, A peut librement choisir l’un des 40 triplets d’axes x, y, z, et la réponse de la particule b est indépendante de ce choix.

C’est le libre arbitre des expérimentateurs qui permet les choix libres et indépendants du triplet d’axe x, y, z et de l’axe w. Mais dans un référentiel inertiel — appelons-le le référentiel « A d’abord » — l’expérience de B ne se produira qu’un peu plus tard que A, et donc la réponse de A ne peut pas, par causalité temporelle, être affecté par le choix ultérieur de B de w. Dans un référentiel « B d’abord » la situation est inversée, justifiant la dernière partie de MIN.

Démonstration :

Les conditions de l’expérience sont les suivantes : 

• les expérimentateurs A et B sont séparés dans l’espace par une distance suffisante pour que les choix et conditions de l’expérience faites par A respectivement B n’interfèrent par sur B respectivement A.
• A et B vont faire des mesures de spin sur une paire de particule a et b qui sont intriquées :  l’expérimentateur A fait des mesures sur a et B sur b.
• A choisit de faire les mesures de spin de la particule a selon 3 axes x, y, z qui sont l’un des 40 triplets de E₄₀ construits à partir de la configuration de Pères. La réponse (le carré du spin) suivant ces 3 axes sera (1,0,1), ou (1,1,0), ou (1,0,1).
• B choisit de la mesure de spin de la particule b selon l’axe w qui est l’un des 33 axes de la configuration de Pères. La réponse (le carré du pin) suivant cet axe sera 0 ou 1.

Nous supposons vrais les 3 axiomes et raisonnons par l’absurde en faisant l’hypothèse que les particules en question n’ont pas leur libre arbitre, c’est-à-dire :

• que la réponse (i, j, k) d’une particule a à la triple expérience de mesure suivant les axes x, y, z est donnée par une fonction de plusieurs propriétés α₁, α₂, … définies dans un repère inertiel F et dont l’état est défini antérieurement à cette réponse. Nous noterons cela sous la forme θ_Fa(α) = réponse à l’expérience = détermination du triplet qui sortira parmi les 3 possibles (0,1,1) ou (1,0,1) ou (1,1,0) (pour alléger la notation a représente ici l’ensemble des propriétés α_i)
• que la réponse de la particule b suivant la direction w (réponse qui est soit 0 soit 1) est donnée par une fonction de plusieurs propriétés β₁, β₂, … définies dans un repère inertiel G possiblement différent de F et dont l’état est défini antérieurement à cette réponse. Ce que nous noterons de la même façon : θ_Gb(β) = réponse à l’expérience = 0 ou 1.

A partir de maintenant, nous pouvons supposer qu’aucun nouveau bit d’information n’influence les réponses des particules, et donc que α et β sont des fonctions des choix des expérimentateurs respectifs et des événements antérieurs à ces choix. Il se peut qu’une des propriétés α varie aussi selon les axes x, y, z et elle peut, ou non, varier aussi avec w. Dans tous les cas, que la fonction varie avec eux ou non, nous allons voir que nous pouvons introduire tous les x, y, z, w comme nouveaux arguments et réécrire θ_Fa comme une nouvelle fonction (nous lui donnons le même nom pour plus de commodité) dont les arguments ne sont plus les α_i mais seront x, y, z, w, et des propriétés α_i’ indépendantes de x, y, z, w.

θ_Fa(x, y, z, w ; α’ ) (*) , fonction de x, y, z, w et des propriétés α_i’ indépendantes de x, y, z, w.

En effet, pour les α_i qui dépendent effectivement de x, y, z, w nous pouvons éliminer cette dépendance en injectant à la place les valeurs constantes qui peuvent être prises par x, y, z, w : il y a 40 x 33 = 1320 valeurs de quadruplets possibles pour les x, y, z, w que nous utiliserons. Sinon, pour toute fonction α qui serait purement une fonction α(x, y, z, w) de x, y, z, w, nous pouvons retirer ces fonctions de la partie α dans (*) pour ne laisser dans α’ que des bits d’information indépendants de x, y, z, w.

De la même façon nous pouvons réécrire θ_Gb comme la fonction θ_Gb(x, y, z, w ; β’) de x, y, z, w et des propriétés β’ indépendantes de x, y, z, w.

Pour le choix particulier que fera B, il y a une valeur β₀’ de β’ pour laquelle θ_Gb(x, y, z, w ; β₀’) est défini. Compte tenu de l’indépendance de β’ par rapport à w vue précédemment la fonction θ_Gb(x, y, z, w ; β₀’) peut être définie avec la même valeur β₀’ pour toutes les 33 valeurs de w (le fait que l’axiome MIN permette à B de modifier librement son choix de w rend cela intuitivement clair). Nous remarquons aussi que l’axiome MIN permet de dire que la réponse de la particule b ne peut pas varier en fonction de x, y, z. Donc θ_Gb(x, y, z, w ; β₀’) est seulement fonction de w. Nous écrirons θ_Gb(x, y, z, w ; β₀’) =θ_G0(w).

De la même façon il y a une valeur α₀’ de α’ pour laquelle la fonction θ_F1(x, y, z) = θ_Fa(x, y, z, w ; α₀’) est définie pour les 40 triplets x, y, z et qui est aussi indépendante de w, ce qui permet dès lors d’omettre cet argument. 

Mais par l’axiome TWIN nous avons l’équation :

θ_Fa(x, y, z, w ; α₀’) =  θ_Gb(x, y, z, w ; β₀’), ce qui donne :

θ_F1(x, y, z)  = θ_G0(x) si w = x, θ_G0(y) si w = y, θ_G0(z) si w = z.

Nous avons donc une fonction mathématique θ_Go qui pour chaque axe w de la configuration de Peres attribue la valeur 0 ou 1 (= réponse de la mesure à l’expérience) et telle que ses composantes suivant 2 axes orthogonaux à w vérifient avec w la propriété 101. Cela signifie que la fonction mathématique θ_Go permet d’attribuer la propriété 101 à tous les trièdres de E₄₀. Or nous avons vu dans le chapitre Boîte à outil que cela n’est pas possible. CQFQ.

Conclusion : Sous réserve d’accepter les 3 axiomes, on se doit de conclure qu’il ne peut pas y avoir de fonction mathématique qui décrive ce que va être le résultat de l’expérience, le résultat ne peut pas être une fonction mathématique du passé ou même de l’instant auquel est faite la mesure. Le résultat n’émerge d’aucune logique accessible, d’aucun passé exprimable, comme s’il n’était que le choix de la particule elle-même, ou plus exactement le choix du couple de particule intriqué a, b.

Annexe

Commentaires des auteurs John Conway et Simon Kochel sur le théorème.

A-1) Sur la démonstration elle-même :

Si l’une de ces fonctions θ_Fa(a), ou θ_Gb(b), est influencée par une information « libre » (libre dans le sens où cette information ne résulte pas du choix fait par A sur les directions et événements préalablement à ce choix vu du repère F), alors il y a un instant t₀ au plus tôt, après lequel cette information est disponible pour la particule a. Comme les informations « non libres » sont aussi disponibles à t₀, tous les bits d’information, libres et non libres, ont une valeur définie 0 ou 1 qui entrent en argument de la fonction θ_Fa (de même que θ_Gb). On considère donc que la réponse de la particule a démarré à l’instant t₀. Si en effet, il y a un bit libre qui influence la particule a, l’univers a, par définition, pris une décision libre autour du temps t₀, et l’on attribuera cette décision simplement à la particule a plutôt que de l’attribuer de façon plus précise mais pédante à l’univers qui est en toute proximité de la particule.

(i) Étant donné que la scène observée sur l’écran est le résultat d’une cascade d’événements légèrement antérieurs, il est difficile de définir précisément quand « la réponse » commence vraiment. Nous allons maintenant expliquer pourquoi on peut considérer la réponse de a comme ayant déjà commencé à n’importe quel instant postérieur au choix de A alors que tous les bits d’information libres qui l’influencent sont devenus disponibles à a.

Soient N(a) et N(b) des régions convexes de l’espace-temps juste assez grandes pour être « dans le voisinage des expériences respectives », c’est-à-dire qu’elles contiennent les informations de réglages choisis pour l’appareillage de mesure et les réponses associées de la particule. Notre preuve a montré que si le demi-espace temporel arrière t < t_F déterminé par un temps t_F dans un référentiel F donné est disjoint de N(a), alors l’information disponible qu’il contient n’est pas suffisante pour déterminer la réponse de a. D’un autre côté, si chacun des 2 deux demi-espaces (F et G) contient juste son voisinage respectif, alors bien sûr, ils contiennent chacun déjà les réponses. En faisant varier F et G, cela permet de localiser les décisions libres dans chacun des voisinages, ce qui justifie notre attribution du libre arbitre aux particules elles-mêmes.

(ii) Nous remarquons que nous n’avons pas besoin d’interdire à toute l’information contenue dans le demi-espace G-En-Arrière d’être disponibles pour b, car en fait MIN empêche la fonction θ_Gb de la particule b d’utiliser le choix des directions x, y, z fait par l’expérimentateur A. La raison sous-jacente est bien sûr que la relativité nous permet de voir la situation à partir d’un référentiel B-d’abord, dans lequel le choix de A n’est effectué qu’après la réponse de b, de sorte que A est toujours libre de choisir arbitrairement un des 40 triplets. Cependant, et c’est là notre seule utilisation de l’invariance relativiste, le raisonnement utilisé permet en fait à toute information qui ne révèle pas le choix de A d’être transmise à une vitesse supérieure à celle de la lumière, ou même à l’envers dans le temps.

(iii) Bien que nous ayons exclu la possibilité que θ_Gb puisse varier avec le choix des directions fait par A, il est concevable qu’il puisse néanmoins varier avec la réponse (future!) de a. Cependant, θ_Gb ne peut pas être affecté par la réponse de a à un triplet inconnu choisi par A, puisque la même information est transmise par les réponses (0, 1, 1), à (x, y, z), (1, 0, 1) à (z, x, y) et (1, 1, 0) à (y, z, x). Pour une raison similaire θ_Fa ne peut pas utiliser la réponse de b, puisque l’expérience de B pourrait consister à examiner des triplets orthogonaux u, v, w et rejeter les réponses correspondant à u et v.

(iv) On pourrait objecter que le libre arbitre lui-même pourrait en quelque sorte dépendre du référentiel. Mais notre preuve repose sur le choix libre des directions, qui, puisqu’il se concrétise dans l’orientation de certains appareils macroscopiques, doit être le même que vu de n’importe quel référentiel.

(v) Enfin, nous notons que la preuve présentée implique quatre référentiels inertiels : A-premier, B-premier, F, et G. Ce nombre ne peut être réduit sans affaiblir notre théorème, puisque nous voulons qu’il s’applique aux cadres arbitraires F et G, y compris par exemple ceux dans lesquels les deux expériences sont presque simultanées.

A-2) Sur les conséquences philosophiques du théorème sur la question du libre arbitre vs déterminisme :

Certains lecteurs pourraient s’élever contre notre utilisation du terme « libre arbitre » pour décrire l’indéterminisme de la réponse des particules. Notre attribution provocante de la notion de libre arbitre aux particules élémentaires est délibérée, puisque notre théorème affirme que si les expérimentateurs ont une certaine liberté, alors les particules ont exactement le même genre de liberté. Effectivement il est naturel de supposer que cette liberté (la même notion de liberté que celle attribuée aux particules) est l’explication ultime de la nôtre.

Les humains qui choisissent x, y, z et w peuvent bien sûr être remplacés par un programme informatique contenant un générateur de nombres pseudo-aléatoires. Si nous rejetons comme ridicule l’idée que les particules pourraient être au courant de ce programme, alors notre preuve reste valide. Cependant, le libre arbitre serait toujours nécessaire pour choisir le générateur de nombres aléatoires, seul un déterministe déterminé pourrait soutenir que ce choix a été fixé dès l’aube du temps.

Nous avons supposé que les choix d’orientation des expérimentateurs de la configuration Pères sont totalement libres et indépendants. Cependant, la liberté que nous avons déduite pour les particules est plus limitée, puisqu’elle est limitée par l’axiome TWIN. Nous avons introduit le terme « semi-libre » dans notre article de démonstration dans sa version faible pour indiquer que c’est vraiment la paire de particules qui prend conjointement une décision libre.

Historiquement, ce genre de corrélation a été une grande surprise, que de nombreux auteurs ont tenté d’expliquer en disant que l’une des particules influence l’autre. Cependant, comme nous l’expliquons en détail dans notre première démonstration, la corrélation est relativistiquement invariante, contrairement à toute explication de cette sorte. Notre attitude est différente : suivant le fameux dicton de Newton « Hypotheses non fingo », nous ne tentons aucune explication, mais acceptons la corrélation comme un fait de la vie.

Certains croient que l’alternative au déterminisme est le hasard, et ajoutent que « permettre au hasard d’entrer dans le monde n’aide pas vraiment à comprendre le libre arbitre ». Cependant, cette objection ne s’applique pas aux réponses libres des particules que nous avons décrites. Il est peut-être vrai que les processus stochastiques classiques comme le lancer d’une pièce (vraie) n’aident pas à expliquer le libre arbitre, mais l’ajout du hasard n’explique pas non plus les effets mécaniques quantiques décrits dans notre théorème. C’est précisément la nature « semi-libre » des particules jumelées, et plus généralement de l’enchevêtrement, qui montre que quelque chose de très différent du stochasticisme classique est en jeu ici.

Bien que le théorème du libre arbitre nous suggère que le déterminisme n’est pas une option viable, il nous permet néanmoins de convenir avec Einstein que « Dieu ne joue pas aux dés avec l’Univers ». Dans l’état actuel des connaissances, il est certainement au-delà de nos capacités de comprendre la connexion entre les décisions libres des particules et des humains, mais le libre arbitre d’aucun de ces deux éléments n’est expliqué par le simple hasard.

La tension entre le libre arbitre humain et le déterminisme physique a une longue histoire. Il y a longtemps, Lucretius a fait « dévier » de façon imprévisible ses particules qui auraient été sinon déterministes pour permettre le libre arbitre.

Ce fut en grande partie le grand succès de la physique classique déterministe qui a conduit à l’adoption du déterminisme par tant de philosophes et de scientifiques, en particulier dans les domaines éloignés de la physique actuelle. Cette remarque s’applique également au « compatibalisme », une tentative maintenant inutile de permettre le libre arbitre humain dans un monde déterministe.

Bien que le déterminisme puisse formellement être démontré comme étant cohérent, il n’y a désormais plus de preuve ou évidence qui le soutienne, compte tenu du fait que la physique classique a été remplacée par la mécanique quantique, une théorie non déterministe.

L’importance du théorème du libre arbitre est qu’il montre que ce n’est pas seulement la théorie quantique actuelle, mais le monde lui-même qui est non-déterministe, de sorte qu’aucune théorie future ne peut nous ramener à un univers mécanique.

Bibliographie

1. The strong Free Will Theorem : John Conway, Simon Kochel, notice of the AMS 2009, Volume 56 Number 2.