Enoncé
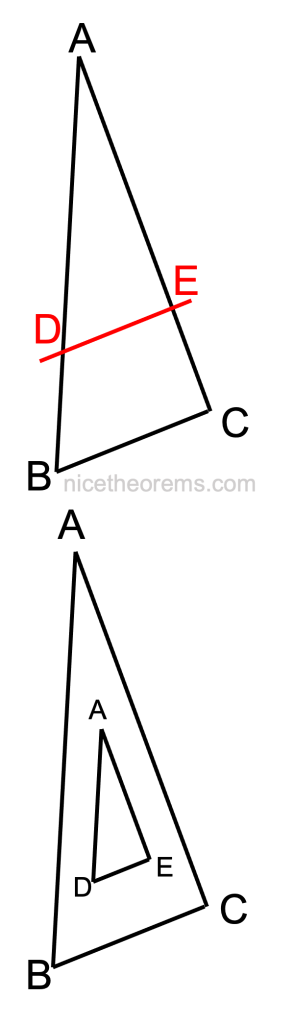
Une droite parallèle à un des côtés du triangle (voir figure ci-contre) coupe ce triangle en un triangle semblable. Cela signifie que le triangle ADE est une homothétie du triangle ABC, autrement dit ADE est juste un modèle réduit du triangle ABC. C’est le triangle ABC vu de plus loin. Comme il s’agit d’un modèle réduit toutes les longueurs sont réduites en proportion :
- AD par rapport à AB
- AE par rapport à AC
- DE par rapport à BC
Enoncé rigoureux : Soit un triangle ABC, et deux points D et E, D sur la droite (AB) et E sur la droite (AC), de sorte que la droite (DE) soit parallèle à la droite (BC). Alors :

Réciproquement, le théorème permet d’établir une condition de parallélisme :
Dans un triangle ABC, supposons donnés des points D et E appartenant respectivement aux segments [AB] et [AC] , si les rapports AD / AB et AE / AC sont égaux, alors les droites (DE) et (BC) sont parallèles.
Histoire
Ce théorème est attribué au mathématicien et philosophe grec Thales de Milet au vie siècle av. J.-C. Selon la légende il aurait calculé la hauteur d’une pyramide en mesurant la longueur de son ombre au sol et la longueur de l’ombre d’un bâton de hauteur donnée. Cependant, aucun texte ancien n’attribue la découverte du théorème à Thalès. Dans son commentaire sur les éléments d’Euclide, Proclus affirme que Thales aurait rapporté ce résultat de son voyage en Egypte. Hérodote rapporte la même chose. C’est la raison pour laquelle ce théorème ne porte pas le nom de Thales dans les pays anglo saxons, on parle plutôt de théorème d’interception, ou de théorème des rayons en Allemagne.
L’intérêt de cette légende est de ramener le théorème a un cas pratique qui permet de le mémoriser, à savoir : la hauteur de la pyramide est à la hauteur du bâton ce que la longueur de l’ombre de la pyramide est à la longueur de l’ombre du bâton.
Démonstration du théorème de Thales
Dans un premier temps nous allons raisonner dans le cas d’un triangle rectangle. La généralisation sera ensuite quasi immédiate.
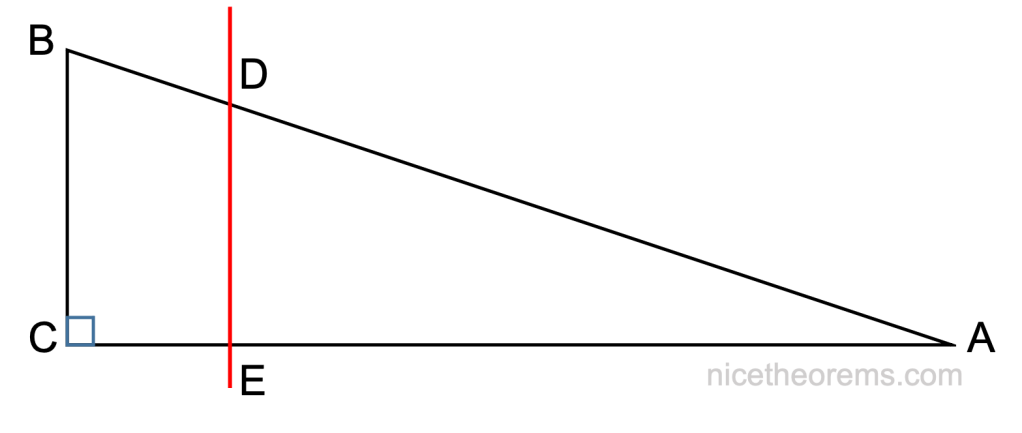
Considérons les 2 triangles (BDE) et (CDE).
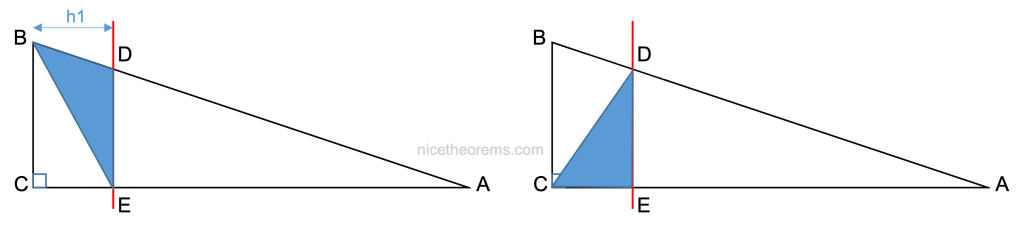
Ces 2 triangles ont même base DE et même hauteur h1 = CE, donc leurs surfaces sont identiques.
On en déduit que les 2 triangles suivants (ABE) et (ACD) ont aussi la même surface puisque l’on a juste adjoint le triangle ADE aux 2 triangles précédents.
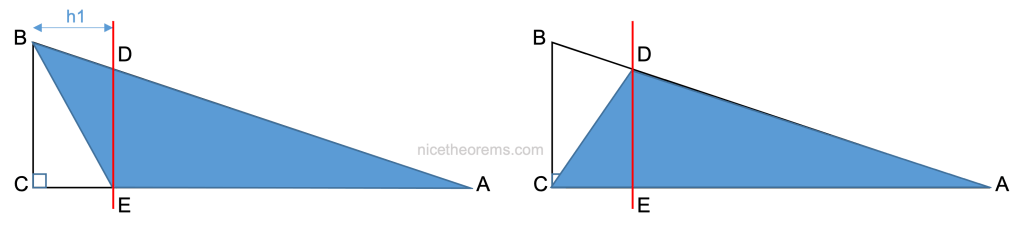
Le premier triangle à pour base AE et hauteur BC.
Le second triangle a pour base AC et hauteur DE.
d’où : AE x BC = AC x DE, et donc :
AE / AC = DE / BC (1)
De plus, le rapport de la surface du triangle (ADE) par rapport à la surface du triangle (ABE) est égale au rapport de la surface du triangle (ADE) par rapport à la surface du triangle (ACD) puisque comme on l’a vu (ABE) et (ACD) ont même surface (voir figure suivante).
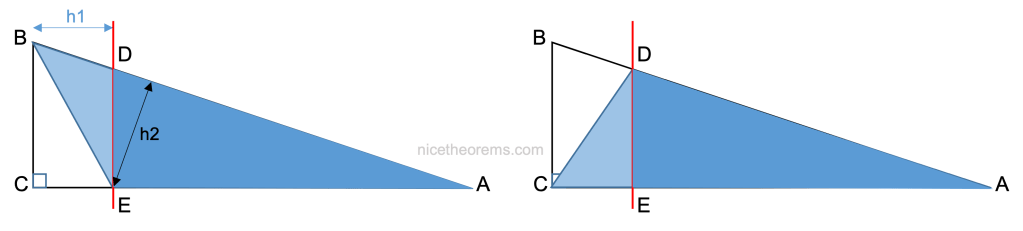
Ce qui donne en notant h2 la hauteur du triangle (ADE) par rapport au côté AD et en remarquant que h2 est aussi la hauteur du triangle ABE par rapport au côté AB :
AD x h2 / AB x h2 = AE x DE / AC x DE
D’où AD / AB = AE / AC (2)
Les résultats (1) et (2) permettent donc d’écrire :

Abordons maintenant le cas général d’un triangle qui ne serait pas rectangle. La perpendiculaire à l’un des côtés qui passe par le somment opposé du triangle permet de le diviser en 2 triangles rectangle (cf figure suivante avec les triangles (ABG) et (ACG) ),
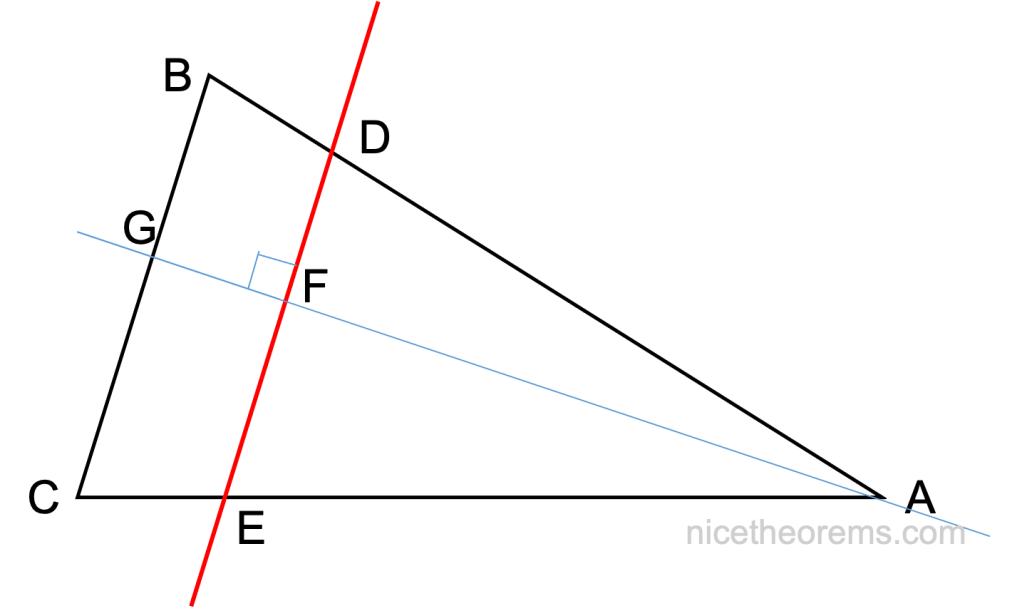
et l’on peut donc écrire en utilisant les résultats acquis dans le cas du triangle rectangle, en considérant le triangle (ABG) :
AD / AB = AF / AG = AE / AC, donc AD / AB = AE / AC. (3)
et par ailleurs DF / BG = AD / AB (4),
De même, avec le triangle (ACG), FE / GC = AE / AC, (5)
de (III), (IV) et (V) on tire DF / BG = FE / GC et FE / DF = GC / BG qui donne aussi (1 + FE/DF) = (1 + GC/BG)
D’où DE / BC = (DF + FE) / (BG + GC) = DF(1 + FE/DF) / BG (1 + GC/BG) = DF / BG. (6)
De (4) et (6) on déduit DE / BC = DF / BG = AD / AB, et avec (3) on retrouvera :

Terminons par la démonstration de la réciproque du théorème : considérons un triangle ABC, et une droite qui coupe les segment AB et AC en respectivement D et E et telle que :

Nous allons voir que cette droite DE est alors forcément parallèle à BC.
Pour cela introduisons la droite parallèle au segment BC qui passe par D. Cette droite coupe le segment AC au point E’ et la droite DE’ est parallèle au côté BC.
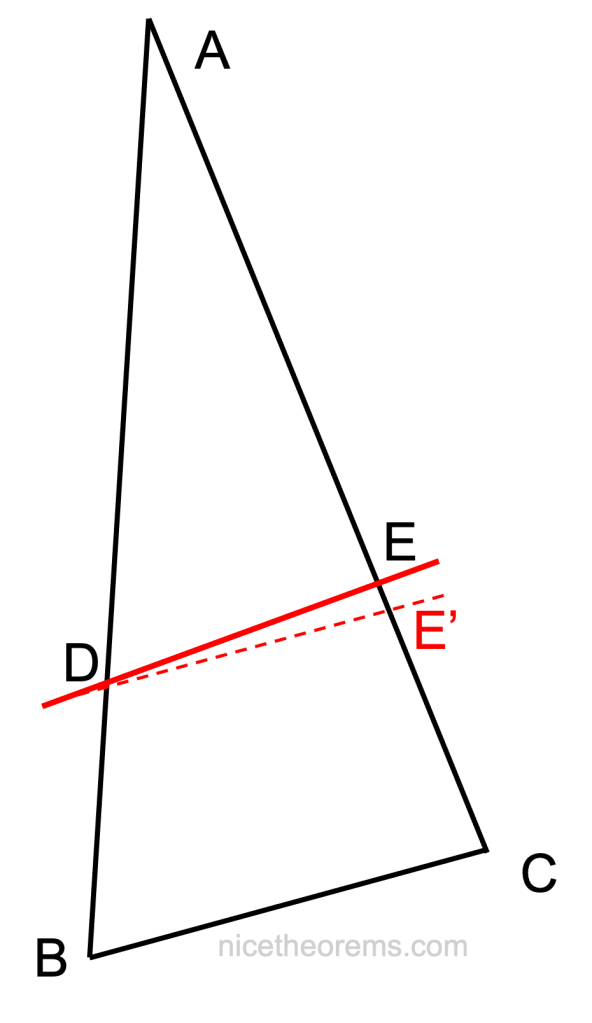
On en déduit, en utilisant le théorème de Thales que l’on vient de démontrer :
AD / AB = AE′ / AC
AD / AB = AE′ / AC par le théorème et AD / AB = AE / AC par hypothèse de départ,
D’où AE‘ = AE, les points E’ et E sont confondus, la droite DE est donc parallèle à la droite BC.
Un théorème bien pratique :
Bien pratique pour mesurer la hauteur d’un objet dont on connait la distance à laquelle on l’observe, juste avec la longueur de son bras et un double décimètre. La hauteur lue sur le double décimètre tenu à bout de bras (hauteur DE) est à la hauteur de l’objet (BC) ce que la distance oeil – bout du bras (AD) est à la distance de l’objet (AB). Cela suppose quand même que l’on connaisse la distance entre son oeil et le bout de son bras, ce qui n’est pas trop difficile.
BC/DE = AB/AD d’où BC = DE*AB /AD autrement dit :
La hauteur de l’objet (ici la hauteur d’une montagne) = Hauteur lue sur la règle*Distance d’observation / Distance oeil-bras.
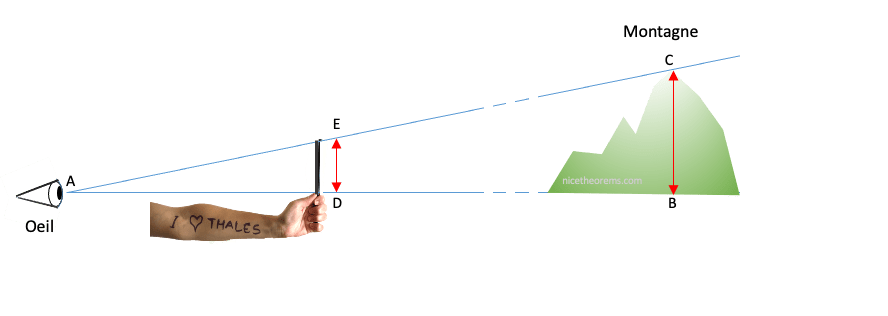
Bien pratique aussi pour déterminer la distance à laquelle se trouve l’objet que l’on regarde et dont on connait la hauteur :
AB = AD*BC/DE
Distance de l’objet = Distance oeil-bras*Hauteur de l’objet / Hauteur lue sur la règle.

