Enoncé

Un entier p strictement plus grand que 1 est un nombre premier si et seulement si il divise (p – 1)! + 1, c’est-à-dire si et seulement si :

(p – 1)! + 1 ≡ 0 (Mod p)

Histoire du théorème

Le premier texte actuellement connu à faire référence à ce résultat est dû au mathématicien arabe Alhazen (965-1039). Il circule en Europe à partir du XVII^e siècle, mais sans être démontré. Au XVIII^e siècle Wilson le redécouvre sous forme de conjecture et partage cette « découverte » avec son professeur Edward Waring qui la publie en 1770. Joseph-Louis Lagrange en présente les 2 premières démonstrations en 1771.

La boîte à outils

Au cours de la démonstration nous aurons besoin de calculer les sommes suivantes :

∑_i=1 ^p-1 i ^k avec p premier > 2 et k entier compris entre 1 et (p – 1).

Calcul de cette somme lorsque k = (p – 1) :

∑_i=1 ^p-1 i ^p-1 ≡ ∑_i=1 ^p-1 1 ≡ (p-1) ≡ -1 (Mod p) en utilisant le petit théorème de Fermat.

Calcul de cette somme dans les autres cas, c’est-à-dire k entre 1 et (p – 2) :

Nous allons montrer que dans tous ces autres cas ∑_i=1 ^p-1 i ^k ≡ 0 (Mod p)

Pour cela, raisonnons par récurrence, à partir de k = 1. 

Montrons que la propriété est vraie pour k  = 1, 

∑_i=1 ^p-1 i ≡ p(p-1)/2 (Mod p)

(p – 1) étant divisible par 2, puisque p est impair (premier > 2), la somme ∑_i=1 ^p-1 i est multiple de p, et l’on a bien ∑_i=1 ^p-1 i ≡ 0 (Mod p).

Montrons maintenant que lorsqu’elle est vraie pour k de 1 à n, elle l’est aussi pour k de 1 à n + 1 (pour autant que n + 2 reste ≤ (p-1), c’est-à-dire n + 1 ≤ (p-2).

Nous cherchons donc maintenant à vérifier que la somme ∑_i=1 ^p-1 i ⁿ⁺¹ ≡ 0 (Mod p) est multiple de p.

Calculons cette somme, en notant a_i les coefficients binomiaux (ils sont forcément entiers puisque résultats du comptage des monômes de degré xⁱ lorsque l’on développe (1 + x)ⁿ⁺²) :

1 ⁿ⁺² = (1 + 0) ⁿ⁺² = 1 ⁿ⁺² + (n + 2).1 ⁿ⁺¹. 0 ¹ + a₂.1 ⁿ. 0 ² + a₃.1 ^n-1. 0³ + …+ a_k.1 ^n-k+2. 0 ^k+ …+ a_n+1.1 ¹. 0 ⁿ⁺¹+ 1.0 ⁿ⁺²

2 ⁿ⁺² = (1 + 1) ⁿ⁺² = 1 ⁿ⁺² + (n + 2).1 ⁿ⁺¹. 1 ¹ + a₂.1 ⁿ. 1 ² + a₃.1 ^n-1. 1 ³ + …+ a_k.1 ^n–k+2. 1 ^k+ …+ a_n+1.1 ¹. 1ⁿ⁺¹+ 1.1 ⁿ⁺²

3 ⁿ⁺² = (2 + 1) ⁿ⁺² = 2 ⁿ⁺² + (n + 2).2 ⁿ⁺¹. 1¹ + a₂.2 ⁿ. 1 ² + a₃.2 ^n-1. 1 ³ + …+ a_k.2 ^n–k+2. 1 ^k+ …+ a_n+1.2 ¹. 1 ⁿ⁺¹+ 1.1 ⁿ⁺²

4 ⁿ⁺² = (3 + 1) ⁿ⁺² = 3 ⁿ⁺² + (n + 2).3 ⁿ⁺¹. 1 ¹ + a₂.3 ⁿ. 1 ² + a₃.3 ^n-1. 1 ³+ …+ a_k.3 ^n–k+2. 1 ^k+ …+ a_n+1.3 ¹. 1 ⁿ⁺¹+ 1.1 ⁿ⁺²

…

k ⁿ⁺² = (k-1 + 1) ⁿ⁺² = (k-1) ⁿ⁺² + (n+2).(k-1) ⁿ⁺¹. 1 ¹ + a₂.(k-1) ⁿ. 1 ² + a₃.(k-1) ^n-1. 1 ³+ …+ a_k.(k-1) ^n–k+2. 1 ^k+ …+ a_n+1.(k-1)¹. 1 ⁿ⁺¹+ 1.1 ⁿ⁺²

…

(p-2) ⁿ⁺² = (p-3 + 1) ⁿ⁺² = (p-3) ⁿ⁺² + (n+2).(p-3) ⁿ⁺¹. 1 ¹ + a₂.(p-3) ⁿ. 1² + a₃.(p-3) ^n-1. 1 ³+ …+ a_k.(p-3) ^n–k+2. 1 ^k+ …+ a_n+1.(p-3)¹. 1 ⁿ⁺¹+ 1.1 ⁿ⁺²

(p-1) ⁿ⁺² = (p-2 + 1) ⁿ⁺² = (p-2) ⁿ⁺² + (n+2).(p-2) ⁿ⁺¹. 1 ¹ + a₂.(p-2) ⁿ. 1 ² + a₃.(p-2) ^n-1. 1 ³+ …+ a_k.(p-2) ^n–k+2. 1 ^k+ …+ a_n+1.(p-2) ¹. 1 ⁿ⁺¹+ 1.1 ⁿ⁺²

(p) ⁿ⁺² = (p-1 + 1) ⁿ⁺² = (p-1) ⁿ⁺² + (n+2).(p-1) ⁿ⁺¹. 1 ¹ + a₂.(p-1) ⁿ. 1 ² + a₃.(p-1) ^n-1. 1 ³+ …+ a_k.(p-1) ^n–k+2. 1 ^k+ …+ a_n+1.(p-1)¹. 1 ⁿ⁺¹+ 1.1 ⁿ⁺²

La somme de tous les termes de gauches de ces égalités = la somme de tous les termes de droites de ces égalités, on obtient donc :

(p-1) ⁿ⁺² = 1 ⁿ⁺² + (n+2) ∑_i=1 ^p-1 i ⁿ⁺¹+ a₂ ∑_i=1 ^p-1 i ⁿ+ a₃ ∑_i=1 ^p-1 i ^n-1 + … + a_k ∑_i=1 ^p-1 i ^n–k+2 + … + a_n+1 ∑_i=1 ^p-1 i ¹+ (p-1)

Tous les termes ∑_i=1^p-1 i ⁿ, ∑_i=1^p-1 i ^n-1 , … , ∑_i=1^p-1 i ^n-k+2, … , ∑_i=1^p-1 i¹, sont ≡ 0 (Mod p), il reste donc :

(p)ⁿ⁺² ≡ 1 ⁿ⁺² + (n+2) ∑_i=1^p-1 i ⁿ⁺¹+ (p-1)   (Mod p)

0 ≡ (n+2) ∑_i=1^p-1 i ⁿ⁺¹ (Mod p)

(n+1) est supposé compris entre 1 et (p-2), donc n+2 est un entier entre 1 et (p-1), il n’est pas divisible par p, et donc

∑_i=1^p-1 i ⁿ⁺¹ ≡ 0 (Mod p).

Les grandes lignes de la démonstration

Dans un premier temps nous montrerons que pour tous p premier : (p – 1)! + 1 ≡ 0 (Mod p).

Ensuite, pour tous p non premier nous verrons que cette égalité n’est jamais vérifiée. On a en fait :

(p – 1)! + 1 ≡ 3 (Mod p), lorsque p = 4

(p – 1)! + 1 ≡ 1 (Mod p) dans tous les autres cas, ce qui veut dire que pour p non premier > 4 :

(p – 1)! ≡ 0 (Mod p)

Démonstration du théorème de Wilson

Première étape : Montrons qui si p est entier non nul alors :

(p – 1)! + 1 ≡ 0 (Mod p)

Pour p = 2 l’égalité est vérifiée, il ne reste plus qu’à la démontrer pour p premier > 2.

Pour cela considérons le polynôme P(x) = (x – 1) (x – 2) (x – 3) …(x – k)…(x – (p – 2)) (x – (p – 1)).

Pour tous x entier non multiple de p, la suite des (p – 1) entiers qui va de (x – 1) à (x – (p – 1)) comprend forcément 1 multiple de p, ce qui implique que :

∀ x entier non multiple de p, P(x) ≡ 0 (Mod p)

P(x)  est un polynôme de degré (p-1), que l’on peut développer sous la forme :

P(x)= x^(p-1) + a₂ x^(p-2) + a₃ x^(p-3)+ … + a_k x^(p–k)+ … + a_p-1 x + (p-1)!

 ∀i ∈ Z/pZ, nous aurons : P(i) ≡ 0 (Mod p). Écrivons cela avec la formule développée du polynôme :

P(1) = 1^(p-1) + a₂ 1^(p-2) + a₃ 1^(p-3)+ … + a_k 1^(p–k)+ … + a_p-1 1 + (p-1)! ≡ 0 (Mod p)

P(2) = 2^(p-1) + a₂ 2^(p-2) + a₃ 2^(p-3)+ … + a_k 2^(p–k)+ … + a_p-1 2 + (p-1)! ≡ 0 (Mod p)

P(3) = 3^(p-1) + a₂ 3^(p-2) + a₃ 3^(p-3)+ … + a_k 3^(p–k)+ … + a_p-1 3 + (p-1)! ≡ 0 (Mod p)

…

P(i) = i^(p-1) + a₂ i^(p-2) + a₃ i^(p-3)+ … + a_k i^(p–k)+ … + a_p-1 i + (p-1)! ≡ 0 (Mod p)

…

P(p-2) = (p-2)^(p-1) + a₂ (p-2)^(p-2) + a₃ (p-2)^(p-3)+ … + a_k (p-2)^(p–k)+ … + a_p-1(p-2) + (p-1)! ≡ 0 (Mod p)

P(p-1) = (p-1)^(p-1) + a₂ (p-1)^(p-2) + a₃ (p-1)^(p-3)+ … + a_k (p-1)^(p–k)+ … + a_p-1(p-1) + (p-1)! ≡ 0 (Mod p)

Et faisons maintenant la somme : P(1) + P(2) + P(3) +…+ P(i) +…+ P(p-2) + P(p-1)

∑_i=1^p-1 P(i) ≡ 0 (Mod p)

Avec la boîte à outils nous savons que ∑_i=1^p-1 i ^p-1≡ p – 1 ≡ -1 (Mod p)

Et que les ∑_i=1^p-1 i ^p-k pour k de 2 à p-1 sont toutes ≡ 0 (Mod p)

La somme se résume donc à :

-1 + (p – 1) (p – 1)! ≡ 0 (Mod p)

C’est à dire : (p – 1)! + 1 ≡ 0 (Mod p)

Seconde étape : Considérons un entier p non nul qui n’est pas premier.

p n’est pas premier, on peut donc écrire p = p_1*p₂ avec p₁ et p₂ 2 entiers < p.

• Cas où p = 4 : (p – 1) ! + 1 ≡ 7 ≡ 3 (Mod 4),
• Cas où p > 4 : comme les nombres 2 et 3 sont premiers et que l’on s’intéresse aux nombres qui ne sont pas premiers et différents de 4, cela signifie que p est ≥ 5.

On a donc, en considérant p₁ comme le plus petit des 2 facteurs :

2 ≤ p₁ qui est lui-même ≤ p₂ , avec au moins une des 2 inégalités strictes, d’où :

p = p_1*p₂  ≤ 2 p₂ puisque p₁ est forcément ≥ 2.

p ≥ 2 p₂ = p₂ + p₂ qui est lui même ≥ p₁+ p₂ avec au moins une des 2 inégalités strictes,

donc finalement p > p₁+ p₂ , ce qui implique que (p – 1)! est divisible par (p₁ + p₂)! qui est lui-même divisible par p_1*p₂ et donc aussi divisible par p .

Cette hypothèse implique donc que (p – 1) ! ≡ 0 (Mod p).

En conclusion, si p > 4 et n’est pas premier alors (p – 1) ! ≡ 0 (Mod p).

Curiosités

Ce théorème donne théoriquement un test pour vérifier si un nombre est premier ou non. Dans la pratique il ne présente pas vraiment d’intérêt pour tester la primarité car il est plus laborieux qu’un crible d’Eratosthène. En revanche, il permet d’écrire différentes formules amusantes qui ne produisent que des nombres premiers (elles sont elles aussi simples qu’inopérantes).

Formules de calcul du nombre de nombres premiers de 1 à n :

On note π(n) la fonction qui donne le nombre de nombre premier inférieur ou égal à n

• Une première formule :

Pour K compris entre 1 et n, en utilisant le théorème de Wilson, il vient, en notant [x] la fonction partie entière de x

[cos (2π ( (p-1)! + 1)/p)] = 1 si p est premier,

[cos (2π ( (p-1)! + 1)/p)] = 0 si p n’est pas premier.

On en déduit :

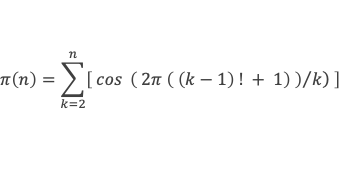
Expressions que l’on peut encore réduire, en utilisant la fonction Gamma (x), notée Γ(x), qui est un prolongement de la fonction factoriel et qui pour k entier donne Γ(k) = (k – 1)!

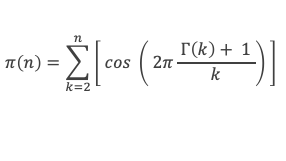
A défaut d’être pratique, l’intérêt de cette formule réside dans sa simplicité.

• Une seconde formule :

Pour p compris entre 1 et n, en utilisant le théorème de Wilson, il vient :

Sin (π (p – 1)!/p) = 0 si p composé ≥ 5

Sin (π (p – 1)!/p) = Sin (π/p) si p est premier. En effet dans ce cas (p – 1)! + 1 = k_*p avec k forcément impair puisque (p – 1)! est pair. On aura donc :

(p – 1) ! = k_*p – 1

π (p – 1) ! = π k_*p – p

π (p – 1)! /p = π k – π/p

Sin (π (p – 1)!/p) = sin (π – π/p) = sin(π/p)

La fonction  π(n) qui donne le nombre de nombre premier inférieur ou égal à n, peut donc s’écrire, pour n ≥ 5 :

Ce qui s’écrit, en utilisant la fonction Γ(k) :

Outre sa relative simplicité, cette formule a le mérite de ne pas faire intervenir de partie entière.

Une Formule de calcul du n^ième nombre premier : noté p_n

En partant de l’expression suivante de p_n, qui exploite le fait que π(k) est < n de 1 à p_n, puis compris entre 1 et < 2 lorsque n varie de p_n à 2[nlogn] + 2 :

On déduit :

Un théorème sur les nombres premiers jumeaux :

Sont dits jumeaux, 2 nombres premiers successifs, c’est à dire tels que p et p + 2 soient tout les deux premiers. Le théorème de Wilson permet d’établir en corollaire le théorème suivant :

p et p + 2 sont premiers jumeaux si et seulement si 4(p – 1)! + 4 + p est divisible par p(p + 2).

Notons déjà que pour p = 3 les nombres p et p + 2 sont premiers jumeaux et la condition est effectivement remplie. De même, pour p = 4, p et p + 2 ne sont pas premiers jumeaux et la condition n’est effectivement pas remplie. Pour la suite, raisonnons avec p ≥ 5.

Montrons d’abord que si p et p + 2 sont premiers, alors 4(p -1) ! + 4 + p est divisible par p(p +2).

D’après le théorème de Wilson, p premier implique :

(p – 1)! + 1 = 0 (Mod p) (I)

D’après le théorème de Wilson, p + 2 premier implique :

(p + 1)! + 1 = 0 (Mod p+2) (II)

Développons (II).

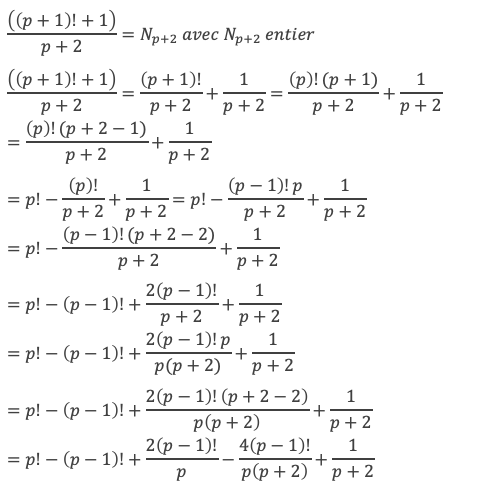
Et comme p est premier :

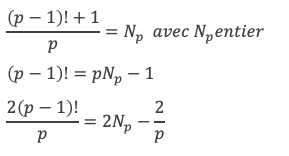
D’où :

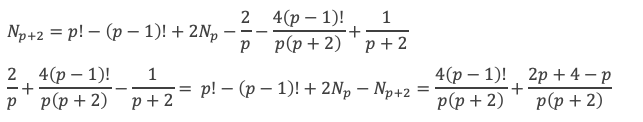
Et comme p! – (p – 1)! + 2 N_p – N_p+2 est un entier, cela implique que 4(p – 1)! + p + 4 est divisible par p(p + 2).

Donc :

p et p + 2 premiers jumeaux ⟹ 4(p – 1)! + 4 + p est divisible par p(p + 2).

Etudions maintenant la réciproque : supposons que p ou bien p + 2 ne soit pas premiers , ou qu’aucun des deux ne le soit.

• Cas p non premier :  pour p ≥ 5 on sait qu’alors (p-1) ! = k p,

 4(p – 1)! + 4 + p = 4k p + 4 + p = 4(k p + 1) + p, qui n’est pas un nombre divisible par p, donc pas divisible par p(p + 2). La propriété de divisibilité n‘est pas remplie.

• Cas p + 2 non premier : on sait qu’alors (p + 1) ! = k (p+2)   (III)
  • Si en plus p n’est pas premier, alors on se retrouve au cas précédent et la propriété de divisibilité ne sera pas remplie.
  • Si p est premier : 

( 4(p – 1)! + 4 + p )*p(p + 1) = 4(p + 1)! + p(p + 1)(p + 4)

= k (p+2) + p(p + 1)(p + 4) = k (p+2) + p(p + 1)(p + 2 + 2)

= ( k + p(p + 1) ) (p+2) + 2p(p + 1)

Donc :

Si 4(p – 1)! + 4 + p était divisible par p(p+2) alors ( 4(p – 1)! + 4 + p )*p(p + 1) devrait être divisible par p + 2, et donc  2p(p + 1) devrait aussi être divisible par (p + 2) or ce n’est pas le cas, donc la propriété de divisibilité n’est pas remplie.

Conclusion : si p et p + 2 ne sont pas premiers jumeaux alors la propriété n’est jamais remplie. C’est-à-dire :

Non [p et p + 2 premiers jumeaux] ⟹ 4(p – 1)! + 4 + p n’est pas divisible par p(p + 2).

Ce qui est équivalent à :

4(p – 1)! + 4 + p est divisible par p(p + 2) ⟹ p et p + 2 premiers jumeaux.

Conclusion :

p et p + 2 sont premiers jumeaux si et seulement si 4(p – 1)! + 4 + p est divisible par p(p + 2).