Enoncé
Soit (a1, a2, a3 …, ak, …, an-1, an) et (b1, b2, b3 …, bk, …, bn-1, bn) 2 n-uplets de nombres réels, l’inégalité de Cauchy-Schwarz s’écrit :
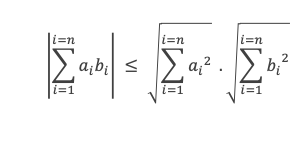
La valeur absolue du produit des n-uplets terme à terme est inférieure au produit des racines de la somme des carrés de chaque n-uplet.
Ou sous une autre forme :
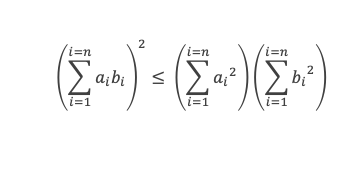
Le carré du produit des n-uplets terme à terme est inférieure au produit de la somme des carrés de chaque n-uplet.
L’inégalité devient une égalité stricte si et seulement si les ai et les bi sont tous proportionnels avec la même proportion, c’est-à-dire que l’on a pour tous i, ai = λbi avec le même λ.
Histoire
Cette inégalité, simple à démontrer, n’a rien d’intuitif. C’est peut-être la raison pour laquelle elle n’apparaît qu’en 1821, dans la publication par Augustin Cauchy de son Cours d’analyse de l’École royale polytechnique.
L’inégalité est élargie au cas des dimensions infinies par Viktor Bouniakovski en 1859, puis par Hermann Schwarz dans un mémoire de 1885.
Démonstration de l’inégalité de Cauchy-Schwarz
Considérons la fonction réelle f(t) qui à t réel associe :
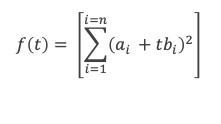
f(t) est une somme de carrés, f(t) est donc toujours positive ou nulle. Développons les carrés des termes, il vient :
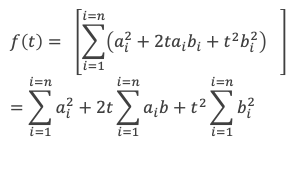
On voit que f(t) s’exprime sous la forme d’un polynôme en t du second degré :
f(t) = A + t B + t2C
Avec
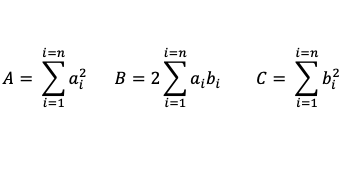
Le cas trivial où le terme C est nul correspond au cas où tous les bi seraient nuls. Dans ce cas l’inégalité est bien vérifiée et l’on a même l’égalité stricte. On se place donc maintenant dans le cas général où C n’est pas nul, c’est-à-dire que l’on est bien dans le cas d’un polynôme de degré 2. Ce polynôme est toujours positif ou nul, donc il ne peut avoir 2 racines distinctes, ce qui signifie que son déterminant est négatif ou nul, donc :
B2 – 4AC ≤ 0, soit B2 ≤ 4AC
Ce qui donne directement l’inégalité cherchée :
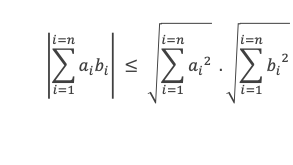
Cas de l’égalité stricte : Montrons maintenant que l’égalité stricte est obtenue si et seulement si les ai et les bi sont tous proportionnels avec la même proportion.
Si pour tous i on a ai = λ bi avec le même λ
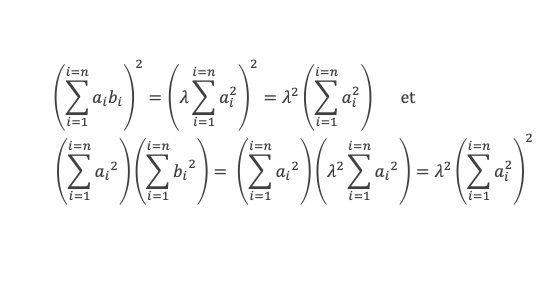
Réciproquement, si l’égalité est vérifiée, c’est que le déterminant du polynôme f(t) est nul, c’est-à-dire que le polynôme a une racine double t0 et que cette racine vérifie :
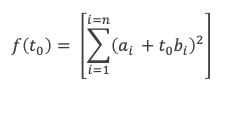
La somme des carrés est nulle, ce qui implique que chaque carré est nul, et donc en notant λ = –t0, tous les ai = λ bi avec le même λ.

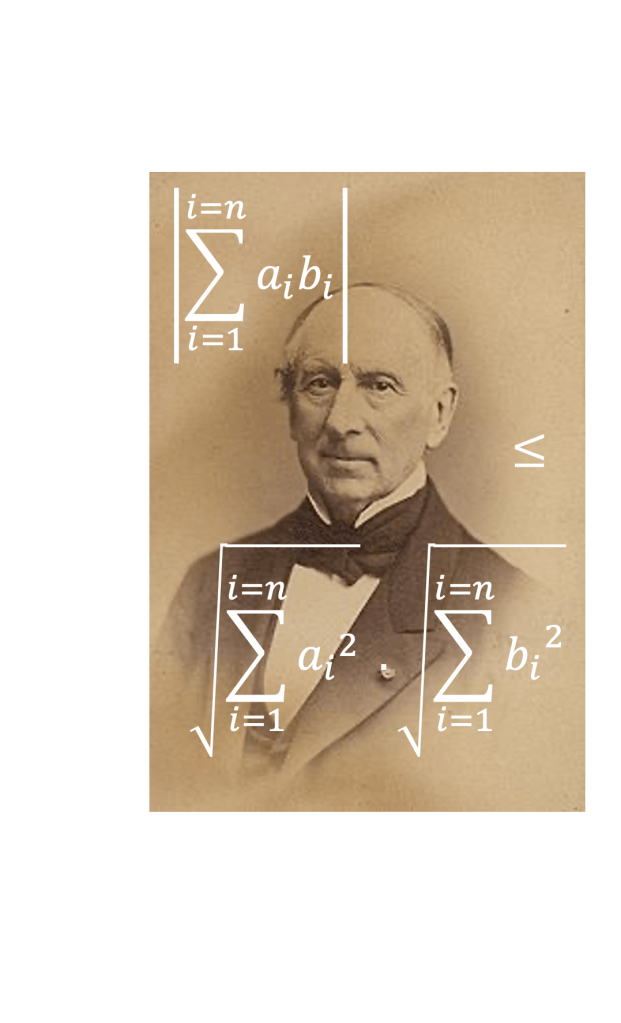
Bonjour, pourquoi le signe du polynome est toujours positif ? B ne peut il pas etre negatif ( B etant la somme des produits ai*bi) et superieur en valeur absolue à A+C ?
J’aimeJ’aime
Bonsoir,
Il faut revenir à la définition du polynôme. La fonction f(t) est par définition une somme de carrés, elle est donc forcément positive ou nulle et jamais négative. Le déterminant du polynôme ne peut être que supérieur ou égal à 0. en effet si le déterminant était négatif il y aurait 2 racines distinctes, et entre ces 2 racines le polynôme prendrait une valeur négative. Pour rappel le déterminant est B au carré -4 A*C.
Cela répond-il a votre question?
J’aimeJ’aime
Petit correctif : le déterminant du polynôme ne peut être que négatif ou nul ( et non positif ou nul comme je l’ai écrit trop rapidement)
J’aimeJ’aime
Super, Merci!
J’aimeJ’aime