
Enoncé
Un polynôme à coefficients complexes de degré n, que l’on écrit
P(x) = a0 xn + a1 xn-1+a2 xn-2 + …+ ak xn-k + …+an-1 x + an
Se décompose en un produit de n monômes sous la forme : P(x) = a0 (x – β1) … (x – βn).
Ici, la famille des βk, pour k variant de 1 à n, est celle des racines. Certains nombres βk peuvent être égaux, on parle alors de racines multiples.
Histoire du théorème
Un premier énoncé correct du théorème est donné par Albert Girard qui en 1629 dans son traité intitulé Inventions nouvelles en l’algèbre, annonce que :
« Toutes les équations d’algèbre reçoivent autant de solutions que la dénomination de la plus haute quantité le démontre. »
Par solutions, il inclut celles en nombres ‘’imaginaires’’, mais à cette époque la notion de nombres complexes n’est pas claire. Cette idée est reprise par René Descartes qui utilise pour la première fois le terme imaginaire, pour qualifier des racines. Ce théorème, fondamental pour l’algèbre, a dès lors souvent été considéré comme acquis, sans pour autant être démontré.
En 1746 Jean le Rond D’Alembert exprime le besoin de démontrer le théorème fondamental de l’algèbre. Son but est de démontrer l’existence d’une décomposition en éléments simples de n’importe quelle fonction rationnelle, afin d’en obtenir des primitives. Si le monde mathématique admet immédiatement le bien-fondé de la nécessité d’une démonstration, l’approche de D’Alembert ne convainc pas. Elle est incomplète.
Leonard Euler puis Joseph-Louis Lagrange se penchent ensuite successivement sur la question, mais sans aboutir. Puis c’est le tour de Gauss qui présente une première preuve en 1799 mais elle est encore incomplète.
En 1814, un amateur suisse du nom de Jean-Robert Argand présente une preuve à la fois solide et simple fondée sur le canevas de d’Alembert. Un an plus tard, Gauss présente une deuxième preuve, qui fait appel à la démarche d’Euler et de Lagrange, et qui est cette fois rigoureuse, mais plus tardive que celle d’Argand. Les deux seules hypothèses que fait Gauss sont (i) toute équation algébrique de degré impair a une racine réelle ; (ii) toute équation quadratique à coefficients complexes a deux racines complexes.
Cauchy, dans son cours d’Analyse pour l’Ecole Polytechnique (1821) présente une preuve inspirée de celle d’Argand. La démonstration exposée dans cet article reprend l’essentiel de la formulation de Cauchy, avec une mise en forme plus moderne.
Boîte à outils
A et B étant 2 nombres complexes, on peut les écrire sous la forme A = u1 + i v1, B = u2 + i v2 , avec u1, u2, v1, v2 nombres réels. On note ‖A‖ la norme de A, définie par ‖A‖ = (u12 + u22)1/2
On a toujours : ‖A + B ‖ ≤ ‖A‖ + ‖B‖, en effet :
‖A + B‖2 = ( (u1 + u2)2 + (v1 + v2)2 ) = u12 + u22 + v12 + v22 + 2 (u1 u2 + v1 v2) = ‖A‖2 + ‖B‖2 + 2 (u1 u2 + v1 v2) ≤ ‖A‖2 + ‖B‖2 + 2 (u12 + v12)1/2 (u22 + v22)1/2 d’après l’inégalité de Cauchy Schwartz (cf article Démonstration de l’inégalité de Cauchy-Schwartz)
D’où : ‖A + B‖2 ≤ ‖A‖2 + ‖B‖2 + 2 ‖A‖ * ‖B‖ = ( ‖A‖ + ‖B‖ )2, et comme tous les termes sont positifs : ‖A + B‖ ≤ ‖A‖ + ‖B‖
On a également : ‖A*B‖ = ‖A‖ * ‖B‖, en effet :
‖A*B‖ = ‖(u1 + i v1)*( u2 + i v2)‖ = ‖(u1 u2 – v1 v2) + i (u1 v2 + v1 u2)‖ = ( (u1 u2 – v1 v2)2 + (u1 v2 + v1 u2)2)1/2 = ( (u1 u2)2 + (v1 v2)2 + (u1 v2)2 + (v1 u2)2 )1/2 = ( (u12 + v12)*(u22 + v22) )1/2 = ‖A‖ * ‖B‖
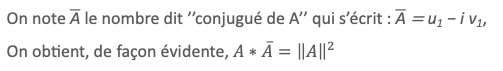
Les grandes lignes de la démonstration
Dans un premier temps nous montrons que tout polynôme P(x) de degré entier > 0 admet forcément au moins 1 racine x0.
Et ensuite que si x0 est racine de P(x) alors (x – x0) divise P(x), c’est-à-dire P(x) = (x – x0) * Rn-1(x) avec Rn-1(x) de degré n-1.
On en déduit donc que tout polynôme de degré n > 0 peut être décomposé sous la forme :
P(x) = (x – x0) * Rn-1(x) avec Rn-1(x) de degré n-1.
La preuve de la décomposition de P(x) en un produit de n monômes s’obtient par récurrence sur n :
La propriété est vraie pour n = 1, et si elle est vraie pour les polynômes de degré n-1 alors le polynôme P(x) peut s’écrire, comme on vient de le voir, P(x) = (x – x0) * Rn-1(x) avec Rn-1(x) de degré n-1.
La propriété étant vraie pour le degré n-1, Rn-1(x) se décompose en un produit de n-1 monômes, et donc P(x) se décompose en produit de n monômes.
Démonstration du théorème fondamental de l’algèbre
Soit P(x) polynôme de degré n entier > 0
P(x) = a0 xn + a1 xn-1+a2 xn-2 + …+ ak xn-k + …+an-1 x + an, avec ak coefficients complexes, et a0 non nul.
Première étape : Montrons que le polynôme P(x) admet forcément au moins 1 racine.
En posant x = u + i v, l’équation P(x) = 0 peut être réécrite sous la forme f(u,v) + i g(u,v) = 0 avec f et g polynômes à coefficients réels, de degré n des 2 variables réelles u et v.
P(x) = 0 ⟺ f(u,v) + i g(u,v) = 0 ⟺ f(u,v) = 0 et g(u,v) = 0 ⟺ f2(u,v) + g2(u,v) = 0
On note pour la suite F(u,v) la fonction f2(u,v) + g2(u,v). Le problème revient donc à démontrer que la fonction F(u,v) qui est une fonction continue et dérivable de u et v, s’annule.
F(u,v) étant une fonction continue et dérivable dont la valeur inférieure est bornée (positive), elle possède un minimum A réel positif ou nul. Soient u0 et v0 les valeurs réelles qui donnent A, et x0 le nombre complexe associé = u0 + i v0. On a f2(u0,v0) + g2(u0,v0) = A, c’est à dire :
‖P(x0)‖2 = A (1).
Nous allons voir maintenant que si A n’est pas nul, alors l’espace entre 0 et A permet de construire à proximité du nombre complexe x0 un complexe (x0 + δx) tel que ‖P(x0 + δx)‖2 < A.
Commençons par calculer P(x0 + δx) pour δx quelconque
P(x0 + δx) = a0 (x0 +δx)n + a1 (x0 +δx) n-1+ a2 (x0 +δx) n-2 + … + ak (x0 +δx) n-k + … + an-1 (x0 +δx) + an
Ce qui donne, en développant chacun des termes (x0 +δx)i, un polynôme de degré n en δx que l’on peut écrire sous la forme :
P(x0 +δx) = b0 δxn + b1 δxn-1 + b2 δxn-2 + … + bk δxn-k + … + bn-1 δx + bn , avec bk nombres complexes qui sont des fonctions de x0 et des aj.
Pour δx = 0 on a P(x0 + 0) = bn , donc ‖P(x0)‖ = ‖bn‖, mais on a aussi ‖P(x0)‖2 = A d’après (1)
Donc ‖bn‖2 = A (2).
Pour bien faire apparaître le raisonnement on suppose pour la suite que bn-1 est non nul (on considèrera ultérieurement le cas où bn-1 est nul). Soit maintenant C, un nombre complexe défini par :
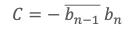
On a en multipliant de chaque côté par bn-1 qui n’est pas nul :
bn-1 C = – ‖bn-1‖2 bn (3).
Et choisissons pour δx la valeur δx = λ C avec λ réel quelconque non nul, il vient :
‖P(x0 + λ C)‖ = ‖b0 (λ C)n + b1 (λ C)n-1 + b2 (λ C)n-2 + … + bk (λ C)n-k + … + bn-1 (λ C) + bn‖
= ‖b0 λn Cn + b1 λn-1 Cn-1 + b2 λn-2 Cn-2 + … + bk λn-k Cn-k + … + bn-2 λ2 C2 + bn-1 λ C + bn‖ , et en utilisant (3)
= ‖b0 λn Cn + b1 λn-1 Cn-1 + b2 λn-2 Cn-2 + … + bk λn-k Cn-k + … + bn-2 λ2 C2 – λ‖bn-1‖2 bn. + bn‖
≤ ‖b0 λn Cn + b1 λn-1 Cn-1 + b2 λn-2 Cn-2 + … + bk λn-k Cn-k + … + bn-2 λ2 C2‖ + ‖bn‖*‖1 – λ‖bn-1‖2‖
Pour λ tel que 0 < λ < Min ( 1/ ‖bn-1‖2 , 1) , et sachant que λ < 1 cela donne, avec (2) :
‖P(x0 + λ C)‖ ≤ λ2‖b0 Cn + b1 Cn-1 + b2 Cn-2 + … + bk Cn-k + … + bn-2 C2‖ + √A*(1 – λ‖bn-1‖2)
‖P(x0 + λ C)‖ ≤ λ2 Σk‖bk Cn-k‖ + √A*(1 – λ‖bn-1‖2)
Si A non nul, comme ∑k ‖bkCn-k ‖, que l’on note D, ne peut pas être nul car C n’est pas nul et les bi ne peuvent être tous nuls avec un polynôme de degré > 1, on peut choisir 0 < λ < √A ‖bn-1‖2 / D , et on obtient alors :
‖P(x0 + λ C)‖ ≤ λ2D + √A*(1 – λ‖bn-1‖2) = λ(λD) + √A*(1 – λ‖bn-1‖2)
= λ(√A ‖bn-1‖2) + √A*(1 – λ‖bn-1‖2) < √A
Comme ‖P(x0 + λ C)‖ et √A sont positifs, ‖P(x0 + λ C)‖ < √A ⟹ ‖P(x0 + λ C)‖2 < A
Or A était censée être la valeur Min de ‖P(x)‖2. Donc l’hypothèse A non nul ne peut être réalisée, il existe forcément x0 = u0 +i v0 tel que f2(u0,v0) + g2(u0,v0) = 0, et donc tel que P(x0) = 0.
Nous avons conduit la démonstration en supposant que bn-1 était non nul. Nous allons maintenant traiter le cas général où cette condition n’est pas imposée.
P(x0 +δx) = b0 δxn + b1 δxn-1 + b2 δxn-2 + …+ bk δxn-k + …+ bn-m δxm + bn, où m est la plus petite puissance positive telle que bn-m soit non nul. Précédemment nous avions fait l’hypothèse m = 1
Nous définissons cette fois C par :

Nous aurons bn-m Cm = – ‖bn-m‖2 bn (4), et de nouveau choisissons δx = λ C avec λ réel quelconque non nul.
‖P(x0 + λ C)‖ = ‖b0 (λ C)n + b1 (λ C)n-1 + b2 (λ C)n-2 + … + bk (λ C)n-k + … + bn-(m+1) (λ C)m+1 + bn-m (λ C)m + bn‖
= ‖b0 λn Cn + b1 λn-1 Cn-1 + b2 λn-2 Cn-2 + … + bk λn-k Cn-k + … + bn-(m+1) λm+1 Cm+1 + bn-m λm Cm + bn‖
= ‖b0 λn Cn + b1 λn-1 Cn-1 + b2 λn-2 Cn-2 + … + bk λn-k Cn-k + … + bn-(m+1) λm+1 Cm+1– ‖bn-m‖2 bn λm + bn‖
≤ ‖b0 λn Cn + b1 λn-1 Cn-1 + b2 λn-2 Cn-2 + … + bk λn-k Cn-k + … + bn-(m+1) λm+1 Cm+1‖ + ‖– ‖bn-m‖2 bn λm + bn‖
≤ ‖b0 λn Cn + b1 λn-1 Cn-1 + b2 λn-2 Cn-2 + … + bk λn-k Cn-k + … + bn-(m+1) λm+1 Cm+1‖ + ‖bn‖*‖ 1 – λm‖bn-m‖2‖
Pour λ tel que 0 < λ < Min ( 1/ ‖bn-m‖2, 1) on peut écrire :
‖P(x0 + λ C)‖ ≤ λm+1‖b0 λn-m-1 Cn + b1 λn-1-m-1 Cn-1 + b2 λn-2-m-1 Cn-2 + … + bk λn-k-m-1 Cn-k + … + bn-(m+1) λ0 Cm+1‖ + ‖bn‖*‖ 1 – λm‖bn-m‖2‖ ≤ λm+1 Σk‖bk Cn-k‖+ ‖bn‖*(1 – λm‖bn-m‖2)
Là encore D = ∑k ‖bkCn-k‖ ne peut pas être nul, et on peut choisir 0 < λ < √A‖bn-1‖2 / D et on obtient alors :
‖P(x0 + λ C)‖ ≤ λm+1 D + ‖bn‖*(1 – λm‖bn-m‖2) = λm (λD) + ‖bn‖*(1 – λm‖bn-m‖2)
‖P(x0 + λ C)‖ < λm √A‖bn-1‖2+ √A*(1 – λm‖bn-m‖2)
‖P(x0 + λ C)‖ < √A et donc ‖P(x0 + λ C)‖2 < A
Ce résultat est de nouveau contraire à l’hypothèse selon laquelle A est la valeur min de ‖P(x)‖2. L’hypothèse A non nul conduit toujours à une contradiction. A est donc nul, ce qui veut dire que P(x) a au moins une racine.
Seconde étape :
Si x0 est racine de P(x) alors (x – x0) divise P(x), c’est-à-dire P(x) = (x – x0) * R(x) avec R(x) de degré n-1.
En effet, dans ce cas nous avons P(x) = P(x0) = 0
Donc :
P(x) – P(x0) = (a0 xn + a1 xn-1+ a2 xn-2 + … + ak xn-k + … + an-1 x + an ) – (a0 x0n + a1 x0n-1+ a2 x0n-2 + … + ak x0n-k + … +an-1 x0 + an) = (xn – x0n) + a1( xn-1– x0n-1) + a2( xn-2 – x0n-2) + … + ak (xn-k – x0n-k) + … + an-1 (x – x0)
Pour tout entier j > 2, le polynôme (xj – x0j) est multiple de (x – x0) en vertu de :
(xj – x0j) = (x – x0)*( xj-1 + x0 xj-2 + x02 xj-3 + … + x0k-1 xj-k + … + x0j-2x + x0j-1)
Le cas j = 1 est évident.
On a donc (xn – x0n) + a1 (xn-1– x0n-1) + a2 (xn-2 – x0n-2) + … + ak (xn-k – x0n-k) + … + an-1 (x – x0) = (x – x0) * R(x) avec R(x) de degré n-1
Soit : P(x) = (x – x0) * R(x) avec R(x) de degré n-1.
Nous avons donc montré que tout polynôme P(x) de degré entier > 0 admet forcément au moins 1 racine x0 et que lorsque x0 est racine de P(x) alors (x – x0) divise P(x), c’est-à-dire P(x) = (x – x0) * Rn-1(x) avec Rn-1(x) de degré n-1. On en déduit donc que tout polynôme de degré n > 0 peut être décomposé sous la forme :
P(x) = (x – x0) * Rn-1(x) avec Rn-1(x) de degré n-1.
Il reste à démontrer que P(x) se décompose en un produit de n monômes. Pour cela on opère par récurrence :
- La propriété est vraie pour n = 1,
- Supposons qu’elle soit vraie pour les polynômes de degré n-1 :
Le polynôme P(x) de degré n peut s’écrire, P(x) = (x – x0) * Rn-1(x) avec Rn-1(x) polynôme de degré n-1.
La propriété étant vraie pour le degré n-1, Rn-1(x) se décompose en un produit de n-1 monômes, et donc P(x) se décompose en produit de n monômes. La propriété devient donc vraie pour le degré n.
