Enoncé du théorème

Étant données une équation polynomiale de degré n, avec n entier ≥ 5

Xⁿ + a₁X^n-1 + a₂X^n-2 + …+ a_n-2X² + a_n-1X + a_n = 0

Il n’existe pas de fonction algébrique permettant d’exprimer les racines x_i de l’équation à partir des coefficients a_i.

Attention nuance : le théorème porte sur le cas général des équations de degré n ≥ 5. Il y a des cas particuliers d’équations résolubles par une fonction algébrique, par exemple :

X¹⁰ + a₁X⁵ + a₂ = 0

Qui se résout très bien en utilisant la formule des équations de degré 2.

Le théorème se limite à la recherche d’une solution qui s’exprimerait à l’aide d’une fonction algébrique, c’est-à-dire d’une fonction qui utilise comme opérations les additions, soustractions, multiplications, divisions, puissances nièmes, racines nièmes. L’utilisation de fonctions plus complexes, telles que les fonctions elliptiques, permettent de les résoudre.

Histoire du théorème

La résolution des équations du second degré, donc de la forme X² + a₁X + a₂ = 0 où l’on cherche l’inconnu X, remonte à plus de trois mille ans. Elles sont au centre de l’algèbre babylonienne, dès avant le XVIIIe siècle av. J.-C. 

Au IXe siècle Al-Khwarizmi en fait une étude systématique dans un ouvrage intitulé Abrégé du calcul par la restauration et la comparaison qui, via le mot « restauration » (en arabe : al-jabr) a donné son nom à l’algèbre. 

Il faut attendre le XVIe siècle pour voir apparaître une solution générale aux équations de degré 3, donc de la forme : X³ + a₁X² + a₂X + a₃= 0

Elle est mise au point par l’Italien Tartaglia qui l’utilise lors d’un célèbre concours qui l’oppose à son compatriote Fiore, en 1535. 

En 1545, Jérome Cardan publie Ars Magna (Le Grand Art). Il y expose la méthode de résolution de Tartaglia en lui en attribuant bien la paternité. Il complète son exposé par une justification de la méthode et l’étend à l’ensemble de tous les autres cas. Il publie, à cette occasion, la méthode de résolution de l’équation de degré 4 mise au point par son élève Ludovico Ferrari. L’importance de l’œuvre de Cardan fait que la postérité ne retiendra que son nom et que cette méthode de résolution des équations de degré 3 va porter le nom de méthode de Cardan.

Dans son mémoire de 1771, Lagrange réalise une synthèse de toutes les méthodes utilisées dans le passé pour résoudre l’équation algébrique de petit degré. À partir de cette synthèse, il développe une méthode, qui s’applique aux degrés 2, 3 et 4. Il montre de plus que cette méthode ne peut aboutir dans le cas général si le degré est plus élevé. La question de savoir s’il n’existe pas d’autres méthodes qui fonctionneraient reste néanmoins ouverte. A partir de l’idée de Vandermonde d’utiliser les fonctions symétriques ainsi que les relations entre les coefficients et les racines, il montre l’importance des n! permutations des racines pour la résolution du cas général. Il établit à ce propos deux théorèmes préfigurant la théorie des groupes. Le premier est que les n! permutations d’un n-uplets ont comme image par une fonction de n variables un ensemble dont le cardinal est un diviseur de n!. Ce résultat est un ancêtre de ce que l’on appelle maintenant le théorème de Lagrange sur les groupes. Le deuxième concerne les fonctions qu’il qualifie de semblables et qui sont invariantes par le même sous-groupe de permutation. Ce résultat anticipe les théorèmes sur les suites de sous-groupes que l’on trouve dans la théorie de Galois. La conclusion de Lagrange est pessimiste. Il émet l’idée que la résolution algébrique de l’équation soit impossible. Le chemin est tracé, soit pour trouver une méthode générale de résolution, soit pour montrer l’inexistence d’une telle méthode. La solution réside dans une analyse combinatoire des possibles permutations des racines. 

L’éventuelle impossibilité de la résolution par radicaux du cas général fait son chemin. Paolo Ruffini publie quatre mémoires à ce sujet, en 1799, 1804, puis en 1808 et 1813. Pour la première fois, l’impossibilité est clairement déclarée. Sa tentative pour le prouver suit la démarche de Lagrange et consiste à montrer que l’usage d’une équation auxiliaire ne permet pas, pour le degré 5, d’abaisser systématiquement le degré de l’équation initiale. Il établit que, si une fonction symétrique de cinq variables prend strictement moins de cinq valeurs par permutations des variables, alors elle n’en prend pas plus de 2. Son approche est lacunaire. Rien n’indique qu’une approche radicalement différente de celles décrites par Lagrange ne pourrait aboutir.

Pour conclure de manière définitive, il fallait raisonner différemment que ne l’avaient fait Lagrange ou Ruffini. Niels Abel l’exprime ainsi : « […] on se proposait de résoudre les équations sans savoir si cela était possible. Dans ce cas, on pouvait bien parvenir à la résolution, quoique ce ne fût nullement certain […] Au lieu de demander une relation dont on ne sait pas si elle existe ou non, il faut se demander si une telle relation est en effet possible. » En 1826, Abel part du résultat et suppose qu’il existe une formule, fonction rationnelle de radicaux, qui donne la solution d’une équation de degré 5. Il sait qu’elle est à même d’exprimer 5 racines différentes et qu’en conséquence, elle possède un comportement précis vis-à-vis des permutations des variables, déjà étudiées par Vandermonde, Lagrange puis Cauchy. Il démontre que ce comportement introduit une absurdité.

Ce résultat reste à ce moment fort peu connu. Son article, pourtant envoyé à Gauss, Legendre et Cauchy n’intéressera personne. 

Boîte à outils

La démonstration repose largement sur le concept de symétrie de la fonction par rapport aux variables. Ce que l’on entend par là nécessite quelques explications, à commencer par la notation des variables, et le sens des noms qu’on leur attribue.

Considérons une fonction F de 5 variables. Pour concrétiser la définition de cette fonction, nous avons besoin de donner des noms aux différentes variables, par exemple en les désignant par a, b, c, d, et e, et nous avons besoin d’associer à cette fonction une expression mathématique construite à partir de ces noms de variables. Par exemple :

F(a, b, c, d, e) = a + 3b + 5c + 2d + e.                             (0-1)

Ce que l’on appelle expression de la fonction est en quelque sorte l’algorithme de calcul de cette fonction, en l’occurrence : somme de la première variable avec 3 fois la deuxième, 5 fois la troisième, 2 fois la quatrième, et la cinquième.

Lorsque l’on dit que l’on note les variables a, b, c, d, et e, cela signifie que l’on affecte le nom a à la première variable, le nom b à la seconde variable, le nom c à la troisième, etc…

On aurait pu tout autant choisir d’autres noms pour les variables, par exemple les noms c, d, e, f, g, h et la même fonction s’écrirait :

F(c, d, e, f, g) = c + 3d + 5e + 2f + g.                               (0-2)

F(a, b, c, d, e) = a + 3b + 5c + 2d + e et F(c, d, e, f, g) = c + 3d + 5e + 2f + g désignent la même fonction, bien que les noms des variables soit différents.

L’égalité (0-1) qui associe la notation F(a, b, c, d, e) à l’expression a + 3b + 5c + 2d + e est définie et vraie pour toutes les valeurs que pourraient prendre les 5 variables et quel que soit leur nom. C’est le sens de cette égalité.

D’une façon générale si l’on note F(a, b, c, d, e) la fonction, et E(a, b, c, d, e) l’expression de son calcul (a + 3b + 5c + 2d + e en l’occurrence) alors :

F(a, b, c, d, e) = E(a, b, c, d, e)

Et si l’on change le nom de variable dans F, il faut faire le même changement de nom dans E. Si l’on permute des lettres dans F, il faut permuter les lettres de la même façon dans E pour conserver l’égalité et travailler avec la même fonction. Ainsi, si l’on décide d’appeler la première variable b, et la seconde variable a, sans changer le nom des autres variables, la fonction noté F(b, a, c, d, e) aura pour expression (ou algorithme de calcul) : b + 3a + 5c + 2d + e. Ainsi les fonctions F(a, b, c, d, e) avec l’expression a + 3b + 5c + 2d + e, et F(b, a, c, d, e) avec l’expression b + 3a + 5c + 2d + e sont bien identiques.

Mais attention lorsque l’on attribue une valeur numérique à chaque variable.

Exemple : supposons que l’on affecte au quintuplet (a, b, c, d, e) les valeurs (2, 7, 4, 1, 14)

F(a, b, c, d, e) = a + 3b + 5c + 2d + e avec l’expression (0-1) = F(2, 7, 4, 1, 14) = 2 + 21 + 20 + 2 + 14 = 59

F(b, a, c, d, e) = b + 3a + 5c + 2d + e avec l’expression (0-2) = 7 + 6 + 20 + 2 + 14 = 49

Dans les 2 cas on travaille bien avec la même fonction F, mais dans un cas on calcule F(2, 7, 4, 1, 14) et dans l’autre cas F(7, 2, 4, 1, 14) or la fonction F est telle que F(2, 7, 4, 1, 14) ≠ F(7, 2, 4, 1, 14).

En fait, si l’on permute les variables (en l’occurrence a et b), il faut aussi permuter les valeurs (en l’occurrence 2 et 7), pour retrouver les mêmes valeurs numériques :

b + 3a + 5c + 2d + e = 59 avec (7, 2, 4, 1, 14) et a + 3b + 5c + 2d + e = 59 avec (2, 7, 4, 1, 14)

La fonction F donne bien toujours les mêmes valeurs pour un quintuplet de 5 valeurs numériques données, indépendamment de la façon de nommer les variables, et heureusement. 

Allons plus loin. Considérons 2 fonctions F1 et F2 quelconques telles que pout tous a, b, c, d, e, on ait l’égalité :

F1(a, b, c, d, e) = F2(a, b, c, d, e). (0-3)

Si l’on échange les 2 premières variables, désormais b est la première variable et a la seconde , on aura :

F1(b, a, c, d, e) = F2(b, a, c, d, e)

Et d’une façon générale, toute permutation entre les variables (2 des 5 ou 3 des 5 ou 4 des 5, ou les 5) conservera l’égalité si elle est appliquée identiquement aux 2 termes. C’est à dire par exemple :

F1(b, a, d, e, c) = F2(b, a, d, e, c), ou bien F1(c, e, d, a, b) = F2(c, e, d, a, b)

Ce que l’on peut écrire : F1(Permut(a, b, c, d, e)) = F2(Permut(a, b, c, d, e))

Une autre façon d’assimiler cette notion consiste à d’introduire la fonction K(b, a, c, d, e) = F1(b, a, c, d, e) – F2(b, a, c, d, e). D’après (0-3) la fonction K(a, b, c, d, e) = 0 quelles que soient les valeurs de ses variables. On aura donc K(b, a, c, d, e) = 0, ce qui donne à nouveau F1(b, a, d, e, c) = F2(b, a, d, e, c), ou K(c, e, d, a, b) = 0, ce qui donne à nouveau F1(c, e, d, a, b) = F2(c, e, d, a, b), et d’une façon générale : K(Permut(a, b, c, d, e)) = 0, soit F1(Permut(a, b, c, d, e)) = F2(Permut(a, b, c, d, e)).

Ce résultat trivial sera très utile au paragraphe 3 de la démonstration, où l’on rencontre le cas de l’égalité 

F1(a, b, c, d, e) = F2(a, b, c, d, e) avec F2 vérifiant aussi F2(a, b, c, d, e) = α F1(b, a, c, d, e)      (0-4)

Il permet d’écrire

F1(b, a, c, d, e) = F2(b, a, c, d, e) = α F1(a, b, c, d, e)              (0-5)

Et comme d’après (0-4) F1(a, b, c, d, e) = α F1(b, a, c, d, e), cela donne en remplaçant dans (0-5) 

F1(b, a, c, d, e) = F2(b, a, c, d, e) = α F1(a, b, c, d, e) = α F2(a, b, c, d, e) 

= α² F1(b, a, c, d, e).

Passons à la notion de symétrie. 

Une fonction présente une symétrie si son expression reste inchangée lors d’une permutation de variable. 

Dans le cas de la fonction F(a, b, c, d, e) = a + 3b + 5c + 2d + e, la fonction n’est pas symétrique pour les échanges entres a et b. En effet si l’on permute a et b alors F(b, a, c, d, e) = b + 3a + 5c + 2d + e qui est une expression différente de a + 3b + 5c + 2d + e. Comme on l’a vu au paragraphe précédent, si l’on permute les variables, il faudra aussi permuter les valeurs des variables pour retrouver le même résultat.

D’où, en général, F(b, a, c, d, e) ≠ F(a, b, c, d, e) pour un même jeu de valeurs de (a, b, c, d, e). C’est ce que l’on a vu lors du calcul de F(2, 7, 4, 1, 14) et de F(7, 2, 4, 1, 14).

Cela n’est pas choquant ce comportement est normal lorsqu’il n’y a pas de symétrie, particulière ce qui est le cas généralement des fonctions. En revanche, si l’on considère la même fonction F et que l’on permute les variables a et e, on a alors :

F(e, b, c, d, a) = e + 3b + 5c + 2d + a =  a + 3b + 5c + 2d + e =  F(a, b, c, d, e)

a et e sont symétriques, nous pouvons permuter seulement les noms, ou seulement les valeurs, cela ne change pas le résultat.

F(e, b, c, d, a) =  F(a, b, c, d, e)

Les expressions des 2 fonctions sont identiques, insensibles à la permutation des variables.

F(2, 7, 4, 1, 14) = F(14, 2, 4, 1, 2)

Par symétrique nous entendons que la valeur du terme reste inchangée lorsque l’on permute la valeur d’un x_i avec celle d’un x_j quelque soit les valeurs en jeu.

Une fonction peut avoir plus ou moins de symétrie, par exemple :

Soit G(a, b, c, d, e) = a_*b_*e + d_*c 

G possède 2 types de symétrie : 

• une symétrie d’ordre 2 entre d et c : G(a, b, d, c, e) = G(a, b, c, d, e)
• une symétrie d’ordre 3 entre a, b et e : G(a, b, c, d, e) = G(b, a, c, d, e) = G(e, b, c, d, a) = G(a, e, c, d, b) = G(e, a, c, d, b) = G(b, e, c, d, a)

Notons au passage que la symétrie d’ordre 3 permet de faire une permutation circulaire sur les 3 variables a, b, e, (e prend la place de a qui prend la place de b qui prend la place de e) de sorte que : G(a, b, c, d, e) = G(e, a, c, d, b) = G(b, e, c, d, a)

Pour le corps de la démonstration nous utiliserons non plus les lettres a, b, c, d, e, mais les termes x₁, x₂, x₃, x₄, x₅ comme noms de variable.

Les grandes lignes de la démonstration

Si le problème n’a pas de solution pour les équations de degré 5, il ne peut pas en avoir pour les équations de degré supérieur. En effet, s’il existait une fonction algébrique donnant les racines pour des degré supérieur, par exemple 7, il suffirait de multiplier l’équation de départ par le polynôme (X + 1)²de degré 2 pour se retrouver avec une équation de degré 7. On appliquerait alors la fonction résolvante qui donnerait les 7 racines, à savoir x₁, x₂, x₃, x₄, x₅ et -1, -1 .

La démonstration se concentre donc sur les équations de degré 5.

Partie 1 : les propriétés de la fonction que l’on recherche :

S’il existe une fonction algébrique qui exprime dans le cas général les racines d’une équation de degré 5 en fonction des coefficients a_i de l’équation, alors on verra que cette fonction doit forcément pouvoir s’exprimer aussi comme une fonction h de ces 5 racines, et donc aussi comme une fonction H de polynômes symétriques de ces 5 racines.

x_i = h(a₁, a₂, a₃, a₄, a₅) => h(a₁, a₂, a₃, a₄, a₅) = H(x₁, x₂, x₃, x₄, x₅)

L’expression de H(x₁, x₂, x₃, x₄, x₅) doit forcément donner des valeurs différentes lorsque l’on fait certaines permutations des variables entre elles. En particulier on doit obtenir les 5 racines de l’équation en appliquant successivement des permutations circulaires de 5 variables.

Par exemple si on dispose de l’expression x₁ = H(x₁, x₂, x₃, x₄, x₅), c’est à dire : x₁ – H(x₁, x₂, x₃, x₄, x₅) = 0, alors en remplaçant x₁ par x₂ , x₂ par x₃, x₃ par x₄, x₄ par x₅, x₅ par x₁, on obtient successivement :

x₂ = H(x₂, x₃, x₄, x₅, x₁)

x₃ = H(x₃, x₄, x₅, x₁, x₂)

x₄ = H(x₄, x₅, x₁, x₂, x₃)

x₅ = H(x₅, x₁, x₂, x₃, x₄)

La fonction H ne peut donc pas être invariante pour les permutations circulaires de ses 5 variables.

Partie 2 : Les propriétés d’une fonction algébrique construite à partir des coefficients de l’équation

Toute fonction algébrique h(a₁, a₂, a₃, a₄, a₅)  construite à partir des additions, soustractions, multiplications, divisions, puissances nièmes, et radicaux nièmes appliqués aux coefficients a_i sera telle que H(x₁, x₂, x₃, x₄, x₅) possédera un niveau de symétrie trop élevé, qui laissera H invariante pour les permutations circulaires de ses 5 variables. 

La preuve est apportée en examinant successivement l’effet des racines carrées, puis des racines impaires sur les permutations circulaires de degré 3 et 5. Le résultat de l’examen est que ces racines conservent les propriétés de symétrie circulaire.

Conclusion : Les exigences des parties 1 et 2 sont contradictoires. Le problème est insoluble.

La démonstration

1- Formulation du problème :

Étant donné l’équation générale de cinquième degré à coefficients rationnels de la forme :

f(X) = X⁵ + a₁X⁴ + a₂X³ + a₃X² + a₄X + a₅ = 0                   (1)

Nous voulons, dans le cas général, cinq solutions distinctes, notées x₁, x₂, x₃, x₄, x₅, qui s’exprimeraient sous la forme :

x₁ = h₁(a₁, a₂, a₃, a₄, a₅)

x₂ = h₂(a₁, a₂, a₃, a₄, a₅)

x₃ = h₃(a₁, a₂, a₃, a₄, a₅)                                                        (2)

x₄ = h₄(a₁, a₂, a₃, a₄, a₅)

x₅ = h₅(a₁, a₂, a₃, a₄, a₅)            

C’est-à-dire que nous recherchons 5 expressions qui à partir des coefficients a_i permettent de calculer algébriquement les valeurs des x_i. 

Calculer algébriquement signifie que les opérations de calcul ne font intervenir que des additions, soustractions, multiplications, divisions, puissances nièmes, et radicaux nièmes.

Les coefficients a_i de (1) peuvent être exprimés sous forme de fonction des racines x_i, grâce au fait que la même équation (1) peut être ré-écrite sous la forme (3) suivante :

(X – x₁)(X – x₂)(X – x₃)(X – x₄)(X – x₅) = 0                             (3)

En effectuant le produit des termes de (3), nous obtenons :

X⁵ – (x₁ + x₂ + x₃ + x₄ + x₅) X ⁴ + (x₁x₂ + x₁x₃ + x₁x₄ + … ) X ³ – 

(x₁x₂x₃ + x₁x₂x₄ + x₁x₂x₅ + x₂x₃x₄ + x₂x₃x₅ + … ) X ² +                                       (4)

( x₁x₂x₃x₄ + x₁x₂x₃x₅ + x₁x₂x₄x₅ + x₂x₃x₄x₅) X – (x₁x₂x₃x₄x₅) = 0                                                                                  

Et l’on a, par identité de (1) et (4)

a₁ = – (x₁ + x₂ + x₃ + x₄ + x₅)

a₂ = x₁x₂ + x₁x₃ + x₁x₄ + …

a₃ = – (x₁x₂x₃x₄ + x₁x₂x₃x₅ + x₁x₂x₄x₅ + x₂x₃x₄x₅)                                       (5)

a₄ = (x₁x₂x₃x₄ + x₁x₂x₃x₅ + x₁x₂x₄x₅ + x₂x₃x₄x₅)

a₅ = – (x₁x₂x₃x₄x₅)

Ainsi, chaque coefficient a_i peut être exprimé sous la forme d’un polynôme en (x₁, x₂, x₃, x₄, x₅) dont il faut noter la remarquable propriété de symétrie. Chacun de ces 5 polynômes est symétrique par rapport aux variables x_i, c’est-à-dire invariant pour toute permutation entre les x_i, jusqu’aux permutations circulaires d’ordre 5. Ces 5 polynômes sont nommés polynômes symétriques de base pour la suite.

Considérons l’une quelconque des expressions h_i (i = 1 ou 2 ou 3 …) de (2)

h_i (a₁, a₂, a₃, a₄, a₅) = x_i = fonction h_i de ( 5 termes symétriques par rapport aux x_i) 

Ce que l’on ré-écrit : h_i (a₁, a₂, a₃, a₄, a₅) = x_i = H_i(x₁, x₂, x₃, x₄, x₅) avec H_i une expression algébrique qui est entièrement construite (par addition, multiplication, division, puissances n-ièmes, racines n-ièmes) à partir de termes symétriques par rapport aux x_i.

Mais Hi, bien que composée uniquement de termes symétriques en x_i doit par exécution successive des opérations de calcul algébrique se simplifier et se réduire finalement à une seule variable x_i.

Par symétrique nous entendons que la valeur du terme reste inchangée lorsque l’on permute la valeur d’un x_i avec celle d’un x_j. Voir chapitre Boîte à outils.

Chacun des termes en x_i a le même comportement qu’un autre x_j. Mais alors se pose la question : comment fait H₁ pour produire à la fin la valeur x₁ alors que le calcul n’est fait qu’à partir de termes symétriques, qui ne permettent pas de faire de distinctions entre les x_i ?

Pour le comprendre, examinons ce qu’il se passe avec l’équation du second degré.

f(X) = X² + a₁X + a₂ = 0

a₁ = – (x₁ + x₂)

a₂ = (x₁x₂)

On sait que pour les équations de degré 2, h₁ et h₂ ont pour expression :

h₁ (a₁, a₂) = (-a₁ + √(a₁² – 4a₂) )/2, tandis que h₂ (a₁,a₂) = (-a₁ – √(a₁² – 4a₂) )/2

Intéressons-nous à h₁ :

 (-a₁ + √(a₁² – 4a₂) )/2 = ( x₁ + x₂ + √((x₁ + x₂)² – 4x₁x₂) )/2 = ( x₁ + x₂ + √((x₁ – x₂)²  )/2  , expression qui à ce stade est encore symétrique, c’est à dire qu’elle reste inchangée si l’on remplace x₁ par x₂ et x₂ par x₁. En effet la permutation de x₂ avec x₁ donne alors : ( x₂ + x₁ + √((x₂ – x₁)²  )/2 .

√((x₂ – x₁)²= [ (x₁ – x₂) ou (x₂ – x₁) ] expression qui sous cette forme reste encore symétrique, mais la symétrie disparaît dès que l’on choisit une seule des 2 branches de l’alternative :

H₁(x₁, x₂) = ((x₁ + x₂) + (x₁ – x₂))/2 si l’on choisit (x₁ – x₂) pour racine. Dans ce cas H₁(x₁, x₂) = x₁

H₁(x₁, x₂) = ((x₁ + x₂) + (x₂ – x₁))/2 si l’on choisit (x₂ – x₁) pour racine_. Dans ce cas H₁(x₁, x₂) = x₂

Dans les 2 cas H₁(x₁, x₂) ne fait ressortir qu’une seule valeur, soit x₁ soit x₂ selon le choix de l’alternative ouverte par le traitement de √((x₂ – x₁)². L’expression par H₁ est bien élaborée au départ à partir de termes symétriques qui sont (x₁ + x₂) et ((x₁ + x₂)² – 4 x₁x₂), mais pourtant après calcul littéral elle ne donne qu’une seule des 2 variables (soit x₁ soit x₂), la symétrie a disparu grâce à l’action du radical qui force un choix entre 2 expressions non symétriques. Un radical peut détruire la symétrie de la formule littérale.

Notons qu’une fois le choix fait, l’expression H₁ (x₁, x₂) étant dissymétrique =  ((x₁ + x₂) + (x₁ – x₂))/2, si l’on échange maintenant x₁ et x₂ dans la formule de H₁ on obtient  

H₁(x₂, x₁) = x₂ 

Ainsi on a élaboré une expression H(x₁, x₂) qui permet de calculer une première racine, et telle que H(x₂, x₁) donne la deuxième qui est différente en générale de la première.

Le mécanisme de destruction de la symétrie grâce à des radicaux est la clé pour disposer d’une formule qui donne une variable x₁ à partir de termes symétriques en x₁, x₂, x₃, x₄, x₅.

Les cas des équations de degré 3 et 4 montrent le même comportement de destruction de la symétrie pour aboutir finalement à une réduction de l’expression à une seul variable x_i, cf annexes.

Revenons au cas des équations de degré 5 : 

L’existence d’une expression permettant de calculer les racines à partir des coefficients a_i de l’équation (1) implique donc l’existence d’expressions H_i(x₁, x₂, x₃, x₄, x₅) qui sont entièrement construites à partir de termes symétriques par rapport aux x_i au départ, mais qui par exécution successive des opérations de calcul (ou calcul littéral) se simplifient et se réduisent finalement à une seule des 5 variables x_i.

Prenons par exemple le cas de H₃, H₃(x₁, x₂, x₃, x₄, x₅) = x₃, c’est-à-dire que H₃ est une expression qui à partir des 5 variables d’entrée se simplifie et donne finalement en résultat la 3^ième variable. 

Permutons x₁ et x₃ dans l’expression H₃ : partout où il y avait un x₃ on aura un x₁ et partout où il y avait un x₁on aura un x₃. On dispose ainsi d’une nouvelle expression, et qui est telle que lorsqu’on l’on exécute successivement les mêmes opérations de calcul (= même calcul littéral, ou même algorithme de calcul) qui avaient abouti avec l’expression H₃ à la sortie de la 3^ième variable, on obtiendra cette fois H₃(x₃, x₂, x₁, x₄, x₅) = troisième variable = x₁. Une autre façon de voir le problème est de considérer que H₃(x₁, x₂, x₃, x₄, x₅) donne l’expression de la troisième racine de l’équation :

 (X – x₁)(X – x₂)(X – x₃)(X – x₄)(X – x₅) = 0             

Si l’on considère maintenant l’équation : (X – x₃)(X – x₂)(X – x₁)(X – x₄)(X – x₅) = 0, dans laquelle x₁ est la troisième racine, et x₃ la première, l’application de la même formule H₃ à (x₃, x₂, x₁, x₄, x₅) doit donner x₁.

De même on obtiendra :

H₃(x₁, x₃, x₂, x₄, x₅) = x₂, avec la permutation de x₃ et x₂ dans l’égalité de départ H₃(x₁, x₂, x₃, x₄, x₅) = x₃

H₃(x₁, x₃, x₂, x₄, x₅) = x₂, avec la permutation de x₃ et x₂ dans l’égalité de départ H₃(x₁, x₂, x₃, x₄, x₅) = x₃

H₃(x₁, x₂, x₄, x₃, x₅) = x₄, avec la permutation de x₃ et x₄ dans l’égalité de départ H₃(x₁, x₂, x₃, x₄, x₅) = x₃

H₃(x₁, x₂, x₅, x₄, x₃) = x₅, avec la permutation de x₃ et x₅ dans l’égalité de départ H₃(x₁, x₂, x₃, x₄, x₅) = x₃

On a donc :

H₃(x₁, x₂, x₃, x₄, x₅, x₅) = x₃

H₃(x₃, x₂, x₁, x₄, x₅) = x₁ = H₁(x₁, x₂, x₃, x₄, x₅, x₅)

H₃(x₁, x₃, x₂, x₄, x₅) = x₂ = H₂(x₁, x₂, x₃, x₄, x₅, x₅)

H₃(x₁, x₂, x₄, x₃, x₅) = x₄ = H₄(x₁, x₂, x₃, x₄, x₅, x₅)

H₃(x₁, x₂, x₅, x₄, x₃) = x₅ = H₅(x₁, x₂, x₃, x₄, x₅, x₅)

H₃ est donc une expression de 5 variables qui se simplifie par calcul littéral pour en donner une seule des 5, et elle permet aussi de produire les 5 racines différentes simplement à partir des permutations entre les 5 variables.

La question de la résolution des équations de degré 5 par une fonction algébrique devient : 

Existe-t-il une expression de 5 variables, élaborée à partir d’une combinaison algébrique des 5 polynômes symétriques de ces 5 variables (ceux de (5) ), telles que son expression puisse se simplifier par calcul littéral (c’est-à-dire enchaînement des opérations de calcul formel) pour se réduire finalement à une seule des 5 variables ?

Si une telle expression existe alors elle permet de calculer les 5 racines du polynôme (1) par simple permutation entre les variables. 

On se doute que la simplification du calcul permettant de passer d’une expression symétrique à une expression où il ne reste plus qu’une variable s’appuiera sur l’existence de radicaux. En effet les sommes et produits de termes symétriques donnent des résultats symétriques, et ne permettent pas à eux seuls de casser la symétrie qui est pourtant nécessaire pour faire émerger une seule des 5 variables.

En outre, cette expression, si elle existe en donnant successivement les 5 variables qui la composent, ne peut pas être invariante pour une permutation circulaire de ses 5 variables. Démonstration : 

Les permutations circulaires de base, de 5 variables sont les suivantes : 

1. (x₁, x₂, x₃, x₄, x₅),
2. (x₅, x₁, x₂, x₃, x₄), où x₅ est passé en tête et les autres variables se sont décalées de 1 position
3. (x₄, x₅, x₁, x₂, x₃), où x₄ est passé en tête et les autres variables se sont décalées de 1 position
4. (x₃, x₄, x₅, x₁, x₂), où x₃ est passé en tête et les autres variables se sont décalées de 1 position
5. (x₂, x₃, x₄, x₅, x₁), où x₂ est passé en tête et les autres variables se sont décalées de 1 position

On reste dans le cas où H_i(x₁, x₂, x₃, x₄, x₅, x₅)  donne toujours comme résultat la troisième variable (le raisonnement s’applique tout autant pour les autres H_i), on aura donc, selon les permutations circulaires des 5 variables :

H_i(x₁, x₂, x₃, x₄, x₅) = x₃

H_i(x₅, x₁, x₂, x₃, x₄) = x₂

H_i(x₄, x₅, x₁, x₂, x₃) = x₁

H_i(x₃, x₄, x₅, x₁, x₂) = x₅

H_i(x₂, x₃, x₄, x₅, x₁) = x₄

Si l’expression est invariante par permutation circulaire des 5 variables alors cela signifie que les 5 résultats donnés par H_i devront être identiques, et donc que les 5 racines x₁, x₂, x₃, x₄, x₅, x₅ sont identiques, ce qui n’est évidemment pas le cas en général. 

La fonction que l’on cherche ne peut pas être invariante pour une permutation circulaire de ses 5 variables.

De même la fonction ne peut pas être systématiquement invariante pour toutes les permutations circulaires de 3 variables : en effet, si l’on reprend l’exemple de H_i(x₁, x₂, x₃, x₄, x₅, x₅) = troisième variable = x₃, et que l’on permute circulairement x₁, x₂, x₃ pour donner x₃, x₁, x₂ alors H_i(x₃, x₁, x₂, x₄, x₅) = x₂, puisque x₂ est devenu la troisième variable.

Existe-t-il une expression de 5 variables, élaborée à partir d’une combinaison algébrique des 5 polynômes symétriques de ces 5 variables, telles que son expression puisse se simplifier par calcul littéral (c’est-à-dire enchaînement des opérations de calcul formel) pour se réduire finalement à une seule des 5 variables, sachant que cette fonction ne pourra pas être invariante pour une permutation circulaire de ses 5 variables et qu’elle ne sera pas non plus systématiquement invariante pour les permutations circulaires de 3 variables?

Cette question est une reformulation du problème de départ, et sa réponse est non, comme le montre la suite.

2- Forme générale de l’expression recherchée

La combinaison des opérateurs +, -, /, * pour construire l’expression recherchée va faire appel à des sommes de polynômes rationnels C_ki avec des radicaux de différents ordres de la forme Σ D_{ij *} ^n_ij√Ψ , avec Ψ lui-même aussi de cette forme c’est-à-dire somme de polynômes rationnels C_xy avec des radicaux de différents ordres de la forme Σ D_{xy *} ^n_xy√Z. Cela aboutira à la forme suivante (6) : 

x₁ = H₁(x₁, x₂, x₃, x₄, x₅, x₅) =

avec : n_ki entiers, B_i, C_ki et D_ij des polynômes rationnels des coefficients a_i de l’équation (1). Ces polynômes peuvent donc s’exprimer à partir de combinaisons des 5 polynômes symétriques vus au début de la démonstration.

3- Analyse des radicaux les plus internes :

Considérons les radicaux les plus interne de la formule (termes entourés en rouge dans la formule du paragraphe précédent). Les plus internes signifie qu’ils ne contiennent plus d’autre radicaux dans leur expression, la fonction  mise sous le radical s’expriment donc seulement sous forme de polynômes rationnel des coefficients a_i de l’équation (1).

Désignons par Y le radical ⁿ√P de l’un d’eux :

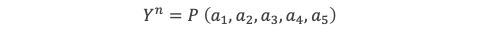
Tout d’abord un tel radical existe forcément dans la formule que l’on cherche, car sinon cela signifierait que H_i est une fonction purement rationnelle des coefficients a_i de l’équation 1, et donc son expression serait purement symétrique des racines x_i ce qui ne pourrait alors produire qu’une seule valeur, indépendante des permutations d’indices. Il n’y aurait qu’une seule valeur de racine possible, or la formule doit en donner 5.

Le terme P de ce radical est quant à lui forcément une expression construite à partir des coefficients a_i de l’équation (1), sans radicaux internes, par définition de Y. Donc à ce stade P est purement symétrique par rapport aux racines (puisque les a_i le sont). P s’exprimera donc par une fonction symétrique de ces racines, que l’on note sous la forme F(x₁, x₂, x₃, x₄, x₅).

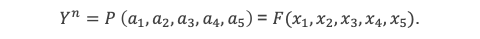
Et on notera 𝜑 (x₁, x₂, x₃, x_4, x₅)  la racine nième de F :

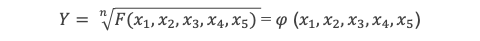
F est symétrique, c’est à dire qu’elle conserve la même expression, quel que soit la permutation de variable que l’on applique. Mais la fonction 𝜑 , elle, ne peut pas être totalement symétrique par rapport aux x_i car sinon cela impliquerait qu’elle soit une fonction des polynômes symétriques de base présentés en (5) et donc qu’elle s’exprime directement sous la forme d’une fonction rationnelle des coefficients a_i (on démontre en effet que toute fonction symétrique d’ordre 5 est forcément une combinaison des 5 polynômes symétriques d’ordre 5 de base). Cela impliquerait que ⁿ√P s’exprime directement comme une fonction des polynômes symétriques de base et donc qu’elle s’exprime directement en fonction rationnelle des coefficients a_i. Autrement dit le terme Y pourrait être exprimé à l’aide des coefficients a_i sans avoir besoin d’utiliser de radical, et donc Y ne serait pas le radical le plus interne de la formule.

Les valeurs de F et de 𝜑ⁿ ne sont pas modifiées par une permutation quelconque des x_i, F et 𝜑ⁿ sont des expressions dans lesquelles tous les x_i se comportent de la même façon et ne peuvent pas être discriminés dans l’algorithme de calcul littéral (l’application du même algorithme de calcul sur F donne toujours le même résultat formel même quand on échange n’importe quel x_i avec n’importe quel x_j). Mais dans le même temps 𝜑(x₁, x₂, x₃, x₄, x₅) ne peut pas être totalement symétrique et son expression littérale change sous l’effet d’au moins une permutation, par exemple entre x₁ et x₂. 

Pourquoi y a-t-il forcément un changement de valeur (et d’expression littérale) pour une permutation entre seulement 2 termes x_i ? On pourrait penser que la dissymétrie n’apparait qu’avec une permutation circulaire d’ordre 3 ou 4 ou 5, et qu’il n’y en a pas pour 2, mais non car toute permutation circulaire d’ordre 3 ou 4 ou 5 se décompose en une succession de permutations entre 2 couples de x_i, ce qui impose de faire déjà apparaitre la dissymétrie à la suite d’une permutation entre 2 racines.

Plus fort, si à partir de F qui est symétrique, on a trouvé un procédé de calcul tel qu’à partir de la permutation par exemple de x₁ et x_2, on produit une dissymétrie sur 𝜑, c’est-à-dire tel que les expressions suivantes (et les valeurs qui en découlent lorsque l’on remplace les variables x_i par leur valeur) vérifient : 

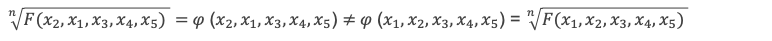
alors le même procédé appliqué à n’importe quel autre couple produira le même effet puisque toutes les variables ont le même comportement et sont indistinctes dans P et que donc tous les couples de variables ont aussi le même comportement, les mêmes propriétés et sont indistincts dans P. Cela signifie que toute permutation de 2 variables x_i, x_j donnera 2 valeurs différentes associées à 2 expressions différentes.

Ce que nous reformulons de la façon suivante :

Pour toute permutation ‘’permut’’ entre 2 des 5 variables (x₁, x₂, x₃, x₄, x₅)

F(x₁, x₂, x₃, x₄, x₅) = F(permut((x₁, x₂, x₃, x₄, x₅)) mais 

𝜑(x₁, x₂, x₃, x₄, x₅) ≠ 𝜑(permut (x₁, x₂, x₃, x₄, x₅))

Raisonnons maintenant sur une permutation entre x₁ et x₂, sachant que le raisonnement sera applicable à toutes les autres permutations :

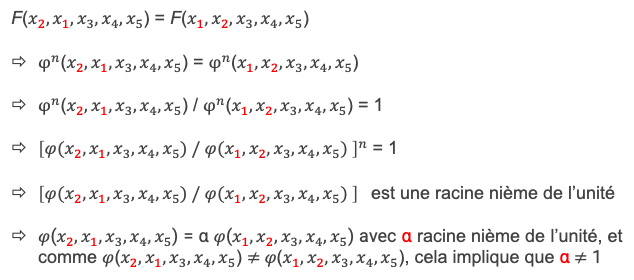
Ce résultat signifie que l’algorithme de calcul de 𝜑 est tel que lorsque l’on échange les 2 premières variables du quintuplet de départ, l’expression résultante par 𝜑 = α fois l’expression par 𝜑 du quintuplet de départ, en l’occurrence (x₁, x₂, x₃, x₄, x₅). Cela signifie donc aussi qu’en partant cette fois du quintuplet (x₂, x₁, x₃, x₄, x₅) l’algorithme de calcul de 𝜑 appliqué à (x₁, x₂, x₃, x₄, x₅) donnera comme expression résultante α fois l’expression par 𝜑 de (x₂, x₁, x₃, x₄, x₅). C’est-à-dire :

𝜑 (x₁, x₂, x₃, x₄, x₅) = α 𝜑(x₂, x₁, x₃, x₄, x₅) avec le même α

Si l’explication à partir de l’algorithme de calcul ne vous suffit pas pour accepter ce résultat, nous pouvons voir la question sous un autre angle : reprenons la formule 𝜑(x₂, x₁, x₃, x₄, x₅) et changeons partout dans cette formule x₂ par y₁, x₁ par y_2, x₃ par y₃, x₄ par y₄, x₅ par y₅ . On a donc :

𝜑(x₂, x₁, x₃, x₄, x₅) = 𝜑(y₁, y₂, y₃, y₄, y₅)

Et en appliquant maintenant sur F(y₁, y₂, y₃, y₄, y₅)  et 𝜑(y₁, y₂, y₃, y₄, y₅) les mêmes procédés de calcul que ceux décrits précédemment pour F(x₂, x₁, x₃, x₄, x₅)  et 𝜑(x₂, x₁, x₃, x₄, x₅) on aura bien.

𝜑(y₂, y₁, y₃, y₄, y₅) = α 𝜑(y₁, y₂, y₃, y₄, y₅), soit 

𝜑(x₁, x₂, x₃, x₄, x₅) = α 𝜑(x₂, x₁, x₃, x₄, x₅) 

Maintenant que l’on est convaincu, des 2 résultats obtenus, à savoir :

𝜑(x₂, x₁, x₃, x₄, x₅) = α 𝜑(x₁, x₂, x₃, x₄, x₅) et 

𝜑(x₁, x₂, x₃, x₄, x₅) = α 𝜑(x₂, x₁, x₃, x₄, x₅)

On tire 𝜑(x₁, x₂, x₃, x₄, x₅) = α² 𝜑(x₁, x₂, x₃, x₄, x₅), 

d’où α² = 1 et donc n=2

En conclusion α² = 1, c’est à dire α = +/-1. D’où un premier résultat remarquable : le radical le plus interne qui se trouve dans la solution générale d’une équation polynomiale résoluble par voie algébrique est forcément une racine carrée. Et c’est bien ce que l’on constate non seulement dans le cas évident de l’équation du second degré, mais aussi dans ceux des équations du troisième et du quatrième degré.

Notre premier Y en général peut donc prendre deux valeurs opposées +𝜑₁ et – 𝜑₁. La première valeur, que l’on choisit arbitrairement de noter +𝜑₁, correspond à l’expression de Y sous la forme 𝜑(x₁, x₂, x₃, x₄, x₅) dans laquelle on remplacerait chaque x_i par sa valeur, et la seconde valeur – 𝜑₁ correspond à l’expression de Y sous la forme 𝜑(x₂, x₁, x₃, x₄, x₅) dans laquelle on remplacerait chaque x_i par sa valeur. Et cela s’applique à toute paire de racines.

De façon plus précise, nous avons démontré que  Y = √P où P est exprimé à partir des coefficients a_i de l’équation (pour rappel P(a₁, a₂, a₃, a₄, a₅) = F(x₁, x₂, x₃, x₄, x₅). Nous savons que P est invariant pour toute permutation des racines x_i. Y ne peut donc prendre que 2 valeurs, notées +𝜑₁ et – 𝜑₁ quelle que soit la permutation considérée. Ces 2 seules valeurs sont aussi le résultat de 2 expressions différentes qui découlent l’une de l’autre en permutant seulement deux racines données : 

𝜑(x₁, x₂, x₃, x₄, x₅) = +𝜑₁ = √P

𝜑(x₁, x₂, x₃, x₄, x₅) = -𝜑₁ = -√P

Et cela s’applique à toute paire de racines.

Pour une autre paire de racine, par exemple x₃ et x_1, les permutations entre x_i et x_j dans l’expression 𝜑(x₁, x₂, x₃, x₄, x₅) ne donneront pas d’autre valeur que : soit +𝜑₁ soit -𝜑_1. En effet, 𝜑(x₃, x₂, x₁, x₄, x₅) = +/- F(x₁, x₂, x₃, x₄, x₅) = +/- √P =  +/- 𝜑₁.

Pour toute permut de 2 racines, 𝜑 (permut (x₁, x₂, x₃, x₄, x₅)) = -𝜑₁ = 𝜑(x₁, x₂, x₃, x₄, x₅)

Conséquence : 

𝜑 (x₁, x₂, x₃, x₄, x₅) ne changera pas de valeur (ni d’expression) lorsque l’on effectuera une permutation circulaire de trois racines (une permutation où, par exemple, x₁, x₂, x₃ devient x₂, x₃, x₁ ou x₃, x₁, x₂), car une telle permutation équivaut à la succession de deux échanges de deux racines, et donc à un double changement de signe.

x₁, x₂, x₃ devient x₂, x₁, x₃ après le premier échange, puis x₂, x₁, x₃ devient x₂, x₃, x₁ après le deuxième échange.

𝜑(x₂, x₃, x₁, x₄, x₅) = 𝜑(x₃, x₁, x₂, x₄, x₅) = 𝜑(x₁, x₂, x₃, x₄, x₅), égalités valables en valeur et en expression.

De même, les permutations circulaires d’ordre 5 sont la combinaison de 4 échanges de 2 racines, et l’on a : 𝜑(x₅, x₁, x₂, x₃, x₄) = 𝜑(x₄, x₅, x₁, x₂, x₃) = 𝜑(x₃, x₄, x₅, x₁, x₂) = 𝜑(x₂, x₃, x₄, x₅, x₁) = 𝜑(x₁, x₂, x₃, x₄, x₅), égalités valables en valeur et en expression.
Cela vaut pour toutes les permutations circulaires d’un nombre impair de racines.

Conclusion de l’analyse des radicaux les plus internes de la formule qui donne les racines de l’équation (1) : Tous les différents termes les plus internes de la formule sont des radicaux second (autrement dit des racines carrées) de la forme √P_i. Ces termes ne peuvent prendre que 2 valeurs différentes et ont des expressions 𝜑(x₁, x₂, x₃, x₄, x₅) qui seront insensibles à des nombres pairs de permutations entre des couples de x_i, c’est-à-dire qu’elles donneront toujours la même valeur lorsque l’on applique un nombre pair de permutation entre 2 variables. Par conséquent les termes les plus internes s’expriment sous la forme √P_i dont l’expression à l’aide des racines est  𝜑(x₁, x₂, x₃, x₄, x₅) et cette expression est telle que les permutations circulaires de trois ou cinq racines, ne changent pas la valeur de ce terme.

4- Analyse des radicaux qui contiennent les radicaux les plus internes :

4-1) Analyse générale :

On s’intéresse maintenant aux radicaux de niveau supérieur aux radicaux les plus internes (cf expressions entourées en rouge).

Posons Q = C_ij + Σ D_{ij *} ^n_ki√P_ki  et  Z = ^n_kx√Q

Z est donc un radical qui contient un radical le plus interne. Dans le paragraphe précédent nous avons vu que ^n_ki√P_ki est en fait : √P_ki = 𝜑 (x₁, x₂, x₃, x₄, x₅) avec 𝜑 fonction rationnelle des racines invariante pour toute permutation circulaire de 3 ou 5 racines.

Tous les éventuels autres radicaux ^n_kj√P_kj qui interviennent dans la somme Σ D_{ij *} ^n_ki√P_ki sont aussi forcément des racines secondes car sinon cela signifierait qu’ils contenaient un radical dans l’expression de P, et que donc le terme le plus interne n’était pas celui que l’on a défini au paragraphe 3. Comme ils n’en contiennent pas, le raisonnement du paragraphe 3 s’applique, ^n_kj√P_kj est donc aussi une racine seconde, son expression ne peut donner que 2 valeurs, et la valeur produite par cette expression sera invariante pour toute permutation de 3 ou 5 racines.

Les différents termes √P_kjsont combinés avec des termes D_ij entièrement symétriques (puisque combinaisons de a_i), sommés entre eux et finalement ajouté à C_ij qui est aussi entièrement symétrique car combinaison de a_i. Cela permet d’affirmer que Q aura une expression qui donnera la même valeur pour toute permutation de 3 ou 5 racines.

A ce stade nous avons donc Z = ^n_kx√Q où Q est une fonction rationnelle des racines,  invariante pour toute permutation de 3 ou 5 racines.

4-2) Cas n_i = 2 :

Si n_i = 2 alors la fonction Z sera encore du même genre, c’est-à-dire fonction rationnelle des racines, invariante pour toute permutation circulaire de 3 ou 5 racines, et cela continuera ainsi tant que la remontée d’un niveau à l’autre de l’expression rencontre des racines secondes (donc y compris des racines quatrièmes). Démonstration :

où √P est définit par l’expression 𝜑(x₁, x₂, x₃, x₄, x₅).

On note G(x₁, x₂, x₃, x₄, x₅) l’expression de Z en fonction des racines x_i : 

G²(x₁, x₂, x₃, x₄, x₅) = C + D 𝜑(x₁, x₂, x₃, x₄, x₅)

Et en notant Q(x₁, x₂, x₃, x₄, x₅) = C + D 𝜑(x₁, x₂, x₃, x₄, x₅),

G(x₁, x₂, x₃, x₄, x₅) = +√Q(x₁, x₂, x₃, x₄, x₅) ou bien -√Q(x₁, x₂, x₃, x₄, x₅)

On remarque que toute permutation de 2 variables dans Q fait changer la valeur de Q, mais Q est invariante pour toute permutation circulaire de 3 ou 5 variables => Q ne prend que 2 valeurs et oscille entre ces 2 valeurs à chaque permutation.

La fonction G peut prendre 2 expressions différentes : soit avec + devant la racine, soit avec -. Nous allons montrer que quelle que soit le choix que l’on fera nous aurons toujours : G(x₁, x₂, x₃, x₄, x₅) ≠ G(x₂, x₁, x₃, x₄, x₅), et cela sera aussi vrai pour toute permutation de 2 variables dans G, mais G restera toujours invariante pour les permutations circulaires de 3 variables, ou 5 variables.

Montrons d’abord que : G(x₁, x₂, x₃, x₄, x₅) ≠ G(x₂, x₁, x₃, x₄, x₅),

Q(x₁, x₂, x₃, x₄, x₅) = C + D 𝜑(x₁, x₂, x₃, x₄, x₅)

Q(x₂, x₁, x₃, x₄, x₅) = C + D 𝜑(x₂, x₁, x₃, x₄, x₅) = C – D 𝜑(x₁, x₂, x₃, x₄, x₅)

Donc, dans le cas général : √Q(x₁, x₂, x₃, x₄, x₅) ≠ √Q(x₂, x₁, x₃, x₄, x₅).

Donc : G(x₁, x₂, x₃, x₄, x₅) ≠ G(x₂, x₁, x₃, x₄, x₅).

Montrons maintenant l’invariance pour les permutations circulaires de 3 variables.

Pour les permutations circulaires de 3 variables, considérons les permutations circulaires sur x₁, x₂, et x₃, sachant que le raisonnement qui suit s’applique pour toute autre permutation circulaire de 3 des 5 variables. Il y a 3 permutations circulaires possible pour ces 3 variables : (x₁, x₂, x₃, x₄, x₅),  (x₃, x₁, x₂, x₄, x₅),  (x₂, x₃, x₁, x₄, x₅) et le passage de l’une à l’autre se construit à partir de 2 des 3 couples de permutations suivant : échange (1,2), échange (1,3), et échange (2,3).

• Construction des permutations circulaires de 3 variables à partir du couple (1,2) et (1,3)

La permutation (1,2) : fait passer de G(x₁, x₂, x₃, x₄, x₅) à G(x₂, x₁, x₃, x₄, x₅)

La permutation (1,3) : fait passer de G(x₂, x₁, x₃, x₄, x₅) à G(x₂, x₃, x₁, x₄, x₅)

On obtient ainsi la troisième permutation circulaire : G(x₂, x₃, x₁, x₄, x₅).

Partons maintenant de G(x₂, x₃, x₁, x₄, x₅) :

La permutation (1,2) : fait passer de G (x₂, x₃, x₁, x₄, x₅) à G(x₁, x₃, x₂, x₄, x₅)

La permutation (1,3) : fait passer de G (x₁, x₃, x₂, x₄, x₅) à G(x₃, x₁, x₂, x₄, x₅)

On obtient ainsi la deuxième permutation circulaire G(x₃, x₁, x₂, x₄, x₅).

• Construction des permutations circulaires de 3 variables à partir du couple (1,2) et (2,3)

La permutation (1,2) : fait passer de G(x₁, x₂, x₃, x₄, x₅) à G(x₂, x₁, x₃, x₄, x₅)

La permutation (2,3) : fait passer de G(x₂, x₁, x₃, x₄, x₅) à G (x₃, x₁, x₂, x₄, x₅)

On obtient ainsi la deuxième permutation circulaire G(x₃, x₁, x₂, x₄, x₅).

Partons maintenant de G(x₃, x₁, x₂, x₄, x₅) :

La permutation (1,2) : fait passer de G(x₃, x₁, x₂, x₄, x₅) à G(x₃, x₂, x₁, x₄, x₅)

La permutation (2,3) : fait passer de G(x₃, x₂, x₁, x₄, x₅) à G(x₂, x₃, x₁, x₄, x₅)

On obtient ainsi la troisième permutation circulaire : G(x₂, x₃, x₁, x₄, x₅).

• Construction des permutations circulaires de 3 variables à partir du couple (1,3) et (2,3)

La permutation (1,3) : fait passer de G(x₁, x₂, x₃, x₄, x₅) à G(x₃, x₂, x₁, x₄, x₅)

La permutation (2,3) : fait passer de G(x₃, x₂, x₁, x₄, x₅) à G(x₂, x₃, x₁, x₄, x₅)

On obtient ainsi la troisième permutation circulaire G(x₂, x₃, x₁, x₄, x₅).

Partons maintenant de G(x₂, x₃, x₁, x₄, x₅) :

La permutation (1,3) : fait passer de G(x₂, x₃, x₁, x₄, x₅). à G(x₂, x₁, x₃, x₄, x₅)

La permutation (2,3) : fait passer de G(x₂, x₁, x₃, x₄, x₅) à G(x₃, x₁, x₂, x₄, x₅)

On obtient ainsi la deuxième permutation circulaire G(x₃, x₁, x₂, x₄, x₅).

Sous l’effet de la permutation (1,2),  G(x₂, x₁, x₃, x₄, x₅) prendra l’une des 2 expressions suivantes : +√Q(x₂, x₁, x₃, x₄, x₅) ou bien -√Q(x₂, x₁, x₃, x₄, x₅). De même sous l’effet de la permutation (1,3) G(x₃, x₂, x₁, x₄, x₅) prendra l’une des 2 expression suivantes : +√Q(x₃, x₂, x₁, x₄, x₅) ou bien -√Q(x₃, x₂, x₁, x₄, x₅). Et enfin idem pour la permutation (2,3).

Il y n’a donc que 2 types de comportements possible (soit +, soit -) pour chacune des 3 permutations. Cela implique qu’au moins 2 des 3 permutations (1,2), (1,3), (2,3) auront le même comportement qui sera soit  + et + , soit – et -.

Supposons que (1,2) et (1,3) aient le même comportement (- et -) :

G(x₂, x₁, x₃, x₄, x₅) = –√Q(x₂, x₁, x₃, x₄, x₅), et

G(x₃, x₂, x₁, x₄, x₅) = –√Q(x₃, x₂, x₁, x₄, x₅)

Comme Q(x₂, x₁, x₃, x₄, x₅) = Q(x₃, x₂, x₁, x₄, x₅) puisque Q est invariante par permutation circulaire de 3 variables, nous obtenons : G(x₂, x₁, x₃, x₄, x₅) = G(x₃, x₂, x₁, x₄, x₅), ce qui donne, en permutant 1 et 3 dans les 2 expressions de l’égalité précédente :

G(x₂, x₃, x₁, x₄, x₅) = G(x₁, x₂, x₃, x₄, x₅) (7)

Et aussi en permutant 1 et 2 puis ensuite 1 et 3 dans cette dernière égalité :

G(x₃, x₁, x₂, x₄, x₅) = G(x₂, x₃, x₁, x₄, x₅) (8)

De (7) et (8) on déduit que les 3 termes G(x₁, x₂, x₃, x₄, x₅), G(x₂, x₃, x₁, x₄, x₅), G(x₃, x₁, x₂, x₄, x₅) sont égaux. Il en serait de même si nous avions choisi (+ et +) comme comportement de (1,2) et (1,3).

Supposons maintenant que cela soit (1,2) et (2,3) qui ont le même comportement (- et -) :

G(x₂, x₁, x₃, x₄, x₅) = –√Q(x₂, x₁, x₃, x₄, x₅)

G(x₁, x₃, x₂, x₄, x₅) = –√Q(x₁, x₃, x₂, x₄, x₅)

Nous obtenons : G(x₂, x₁, x₃, x₄, x₅) = G(x₁, x₃, x₂, x₄, x₅) car Q invariante pout toute permutation circulaire de 3 variables, ce qui donne, en permutant 1 et 2 dans les 2 expressions de l’égalité précédente :

G(x₁, x₂, x₃, x₄, x₅) = G(x₂, x₃, x₁, x₄, x₅)

Et aussi en permutant 1 et 3 puis ensuite 2 et 3 dans cette dernière égalité :

G(x₂, x₃, x₁, x₄, x₅) = G(x₃, x₁, x₂, x₄, x₅)

On obtient de nouveau que les 3 termes G(x₁, x₂, x₃, x₄, x₅), G(x₂, x₃, x₁, x₄, x₅), G(x₃, x₁, x₂, x₄, x₅) sont égaux. Cela serait de nouveau idem si l’on supposait que c’est (1,3) et (2,3) qui ont le même comportement.

L’invariance pour les permutations circulaires de 3 variables est démontrée.

Passons maintenant à la démonstration de l’invariance pour les permutations circulaires d’ordre 5 :

Considérons les permutations circulaires de 5 variables : (x₁, x₂, x₃, x₄, x₅), (x₂, x₃, x₄, x_5, x₁,), (x₃, x₄, x_5, x₁, x₂,), (x₄, x₅ , x₁, x₂, x₃,), et (x₅, x₁, x₂, x₃, x₄). Nous allons montrer que la valeur par G de chacune d’elle est la même. La démonstration se fait en appliquant successivement 2 permutations circulaires de 3 variables sur G, en exploitant le fait que chaque permutation circulaire de 3 variables conserve la valeur de G.

Partons de G(x₁, x₂, x₃, x₄, x₅), et appliquons une permutation circulaire sur (x₁, x₂, x₃). Le résultat est G(x₂, x₃, x₁, x₄, x₅) qui est = G(x₁, x₂, x₃, x₄, x₅) compte tenu de l’invariance aux permutations circulaires de 3 variables.

Appliquons maintenant une permutation circulaire sur les 3 dernières variables (x₁, x₄, x₅) pour les faire passer à (x₄, x_5, x₁)

Le résultat devient G(x₂, x₃, x₄, x₅, x₁) = G(x₂, x₃, x₁, x₄, x₅) = G(x₁, x₂, x₃, x₄, x₅)

Donc G(x₂, x₃, x₄, x₅, x₁) = G(x₁, x₂, x₃, x₄, x₅)

De même en partant de G(x₂, x₃, x₄, x₅, x₁) et en appliquant une permutation circulaire sur les 3 premières variables, puis une permutation circulaire sur les 3 dernières, on montrera G(x₂, x₃, x₄, x₅, x₁) = G(x₃, x₄, x₅, x₁, x₂), puis de la même façon G(x₃, x₄, x₅, x₁, x₂) = G(x₄, x₅, x₁, x₂, x₃), et enfin G(x₄, x₅, x₁, x₂, x₃) = G(x₅, x₁, x₂, x₃, x₄).

Conclusion : si le radical juste au-dessus du radical le plus interne est une racine seconde, la fonction G(x₁, x₂, x₃, x₄, x₅),  issue de ce radical prend 2 valeurs différentes lorsque l’on permute 2 variables, et G(x₁, x₂, x₃, x₄, x₅) est invariante pour les permutations circulaires de 3 variables ou de 5 variables. Cela veut dire que G a de nouveau exactement les mêmes propriétés que la fonction Q au début de ce paragraphe. Au fur et à mesure que l’on remonte l’expression en rencontrant des racines carrées, ces propriétés sont conservées. Cela implique que dans cette remontée on doit finir par rencontrer d’autres radicaux que des radicaux seconds puisse que l’on sait que l’expression des racines que l’on cherche ne peut pas être invariante aux permutations circulaires de 5 variables.

4-2) Cas n_i > 2 :

Supposons donc que la remontée des radicaux finisse par aboutir à un radical n_i > 2.  On peut supposer que n_i est impair car le cas pair a été traité au paragraphe précédent et l’on a vu qu’il donne des expressions invariantes aux permutations circulaires de 3 ou 5 variables.

Nous notons Z ce radical, et avons Z = ^n_i√Q où Q est une fonction rationnelle des racines, invariante pour toute permutation de 3 ou 5 racines.

On note de nouveau G(x₁, x₂, x₃, x₄, x₅) l’expression de Z en fonction des racines x_i.

Nous avons donc un Z qui, en soumettant les racines de l’équation à une permutation circulaire de trois, ou cinq variables, devra pouvoir prendre différentes valeurs, mais telle que l’on ait toujours Zⁿ = Q, avec Q inchangé, puisqu’il est inchangé pour une permutation circulaire de trois, ou cinq variables. 

Considérons une permutation circulaire quelconque de 3 variables, par exemple les 3 premières avec (x₂, x₃, x₁, x₄, x₅) :

Gⁿ(x₂, x₃, x₁, x₄, x₅) = Q =  Gⁿ(x₁, x₂, x₃, x₄, x₅) puisque Q est invariant pour une permutation circulaire de trois variables.

d’où G(x₂, x₃, x₁, x₄, x₅) = α G(x₁, x₂, x₃, x₄, x₅) avec α racine n-ième de l’unité. (9)

Appliquons maintenant une permutation (1,2) puis (1,3) sur chacun des termes de l’égalité précédente, et nous obtenons successivement :

G(x₁, x₃, x₂, x₄, x₅) = α G(x₂, x₁, x₃, x₄, x₅)

G(x₃, x₁, x₂, x₄, x₅) = α G(x₂, x₃, x₁, x₄, x₅) et comme, d’après (9) G(x₂, x₃, x₁, x₄, x₅) = α G(x₁, x₂, x₃, x₄, x₅) nous aurons 

G(x₃, x₁, x₂, x₄, x₅) = α² G(x₁, x₂, x₃, x₄, x₅)    (10)

Appliquons de nouveau une permutation (1,2) puis (1,3) sur l’égalité (10) :

G(x₃, x₂, x₁, x₄, x₅) = α² G(x₂, x₁, x₃, x₄, x₅)  (11)

G(x₁, x₂, x₃, x₄, x₅) = α² G(x₂, x₃, x₁, x₄, x₅)  (12)

D’où d’après (12) et (9) :

G(x₁ x₂, x₃, x₄, x₅) = α² G(x₂, x₃, x₁, x₄, x₅) = α³ G(x₁, x₂, x₃, x₄, x₅)    (13)

Donc α³ = 1, avec α une racine n-ième de l’unité.

De même considérons une permutation circulaire sur les trois dernières variables, par exemple x₁, x₂, x₄, x₅, x₃ :

Gⁿ(x₁, x₂, x₄, x₅, x₃) = Q =  Gⁿ(x₁, x₂, x₃, x₄, x₅) puisque Q est invariant pour une permutation circulaire de trois variables.

d’où G(x₁, x₂, x₄, x₅, x₃)  = β G(x₁, x₂ x₃, x₄, x₅) (14) avec β aussi racine n-ième de l’unité. Nous ne préjugeons pas à ce stade que α et β soit la même racine n-ième de l’unité.

Appliquons une permutation (3,4) puis (3,5) sur chacun des termes de l’égalité, et nous obtenons successivement :

G(x₁, x₂ x₃, x₅, x₄)  = β G(x₁, x₂, x₄, x₃, x₅) 

G(x₁, x₂ x₅, x₃, x₄)  = β G(x₁, x₂, x₄, x₅, x₃) ,

et comme d’après 14 G(x₁, x₂, x₄, x₅, x₃)  = β G(x₁, x₂, x₃, x₄, x₅) nous aurons cette fois:

G(x₁, x₂ x₅, x₃, x₄)  = β² G(x₁, x₂, x₃, x₄, x₅)     (15)

Appliquons de nouveau une permutation (3,4) puis (3,5) sur l’égalité (15) précédente :

G(x₁, x₂ x₅, x₄, x₃)  = β² G(x₁, x₂, x₄, x₃, x₅)

G(x₁, x₂ x₃, x₄, x₅)  = β² G(x₁, x₂, x₄, x₅, x₃) = en utilisant (14) = β³ G(x₁, x₂ x₃, x₄, x₅)

Donc cette fois β³ = 1, avec β une racine n-ième de l’unité.

Dans le même temps nous savons que Gⁿ(x₁, x₂, x₃, x₄, x₅) = Q (x₁, x₂, x₃, x₄, x₅)  avec Q invariant par permutation circulaire de 5 variables.

Considérons maintenant une permutation circulaire quelconque de 5 variables, par exemple : (x₂, x₃, x₄, x₅, x₁).

Appliquons une permutation circulaire de 3 variables sur x₄, x₅, x₁, c’est-à-dire les 3 dernières variables.

G(x₂, x₃ x₁, x₄, x₅)  = β² G(x₂, x₃, x₄, x₅, x₁ )  d’après (15) dans laquelle on a remplacé x₁ par x₂, x₂ par x₃, x₃ par x₄, x₄ par x₅, et x₅ par x₁. On a donc :

G(x₂, x₃, x₄, x₅, x₁ ) = 1/β² G(x₂, x₃ x₁, x₄, x₅) = β G(x₂, x₃ x₁, x₄, x₅) puisque β³ = 1. (16)

Or la relation (12) nous dit : G(x₂, x₃ x₁, x₄, x₅) = 1/α² G(x₁, x₂ x₃, x₄, x₅) = α G(x₁, x₂ x₃, x₄, x₅) puisque α³ = 1.

De (16) et (12) on déduit : G(x₂, x₃, x₄, x₅, x₁ ) = βα G(x₁, x₂ x₃, x₄, x₅). (17)

En décalant d’un rang les variables dans (17) on obtiendra

G(x₃, x₄, x₅, x₁, x₂) = βα G(x₂, x₃ x₄, x₅, x₁) (18), puis en décalant encore successivement d’un rang :

G(x₄, x₅, x₁, x₂, x₃) = βα G(x₃, x₄, x₅, x₁, x₂) (19)

G(x₅, x₁, x₂, x₃, x₄) = βα G(x₄, x₅, x₁, x₂, x₃) (20)

G(x₁, x₂ x₃, x₄, x₅) = βα G(x₅, x₁, x₂, x₃, x₄) (21)

De (17) à (21) on tire :

G(x₂, x₃, x₄, x₅, x₁ ) = βα G(x₁, x₂ x₃, x₄, x₅) = βα (βα (x₅, x₁, x₂, x₃, x₄)) = β³α³ (x₄, x₅, x₁, x₂, x₃) = β⁴α⁴G(x₃, x₄, x₅, x₁, x₂) = β⁵α⁵ G(x₂, x₃ x₄, x₅, x₁)

D’où β⁵α⁵ = 1, et comme β³ = 1 = α³, on en déduit β²α² = 1, et donc βα = 1 puisque β³ α³ = 1.

L’égalité βα = 1 reportée dans les égalités (17) à (21) implique que G est invariant à toute permutation circulaire d’ordre 5.

Nous allons maintenant montrer que α = 1 = β, ce qui impliquera cette fois que G est aussi invariant à toute permutation circulaire d’ordre 3.

Partons de G(x₁, x₂, x₃, x₄, x₅) = G(x₄, x₅, x₁, x₂, x₃) (22) par égalité des permutations circulaires d’ordre 5.

Appliquons l’égalité (14), c’est à dire G(x₁, x₂, x₄, x₅, x₃) = β G(x₁, x₂, x₃, x₄, x₅), en remplaçant dans cette égalité : x₁ par x₄, x₂ par x₅, x₄ par x₁, et x₅ par x₂, on obtient alors l’égalité suivante :

G(x₄, x₅, x₁, x₂, x₃) = β G(x₄, x₅, x₃, x₁, x₂) (23)

Comme on a, par double permutation circulaire d’ordre 5, G(x₄, x₅, x₃, x₁, x₂) = G(x₃, x₁, x₂, x₄, x₅), on obtient en remplaçant G(x₄, x₅, x₃, x₁, x₂) par G(x₃, x₁, x₂, x₄, x₅) dans (23) :

G(x₄, x₅, x₁, x₂, x₃) = β G(x₃, x₁, x₂, x₄, x₅). (24)

Or, d’après (10), G(x₃, x₁, x₂, x₄, x₅) = α² G(x₁, x₂, x₃, x₄, x₅) ce qui permet finalement d’écrire :

G(x₁, x₂, x₃, x₄, x₅) = G(x₄, x₅, x₁, x₂, x₃) d’après (22), = β G(x₄, x₅, x₃, x₁, x₂) d’après (23), = β G(x₃, x₁, x₂, x₄, x₅,) d’après (24), = βα² G(x₁, x₂, x₃, x₄, x₅) d’après (10)

Donc βα² = 1, et comme βα = 1, on en déduit α = 1 et β = 1.

Nous voilà donc rendu au même point qu’au début des paragraphe 4-2 ou 4-3, avec un terme Z = ^n_i√Q où Q est une fonction invariante pour toute permutation de 3 ou 5 racines, et Z est de nouveau invariant par permutations circulaires d’ordre 3 ou 5. La remontée des radicaux ne fait jamais apparaître de terme qui ne serait pas invariant aux permutations d’ordre 5.

4-4) Conclusion :

Pour l’équation de degré 5, les radicaux rencontrés au fur et à mesure que l’on remonte dans l’expression des racines ne permettent jamais de construire une expression qui ne serait pas invariante pour une permutation circulaire d’ordre 5. La forme de la fonction que l’on cherche, c’est à dire une fonction algébrique, ne permet pas d’exprimer les racines des équations de degré 5, ni par conséquent les équations de degré supérieur.

Annexe

Réduction de l’expression de la racine d’une équation de degré 3 jusqu’à obtenir x₁.

On s’intéressera aux équations de la forme X³ + p X + q = 0 (A1), sachant que toute équation de degré 3 peut se ramener à cette forme.

En notant x₁ x₂ x₃ les trois racines distinctes nous avons :

p = x₁ x₂ + x₁ x₃ + x₂ x₃

q = – x₁ x₂ x₃

x₁ + x₂ + x₃ = 0

Une des racines, notons la x₁, est donnée par le calcul de l’expression E suivante :

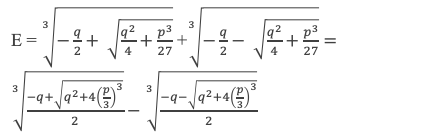
Exprimons q et q² + 4(p/3)³ en fonction des racines :

• D’abord q :

– q =  x₁ x₂ x₃ = x₁²(x₁+ x₂ + x₃)+ x₁ x₂ x₃ = x₁(x₁²+x₁ x₂ + x₁ x₃ + x₂ x₃) = x₁(x₁²+p) = x₁(4x₁²+4p)/4 = x₁(x₁² + 3(x₁²+4p/3) )/4 = (y₁ + y₂)_*( y₁² –y₁y₂ + y₂²) = y₁³ + y₂³, avec :

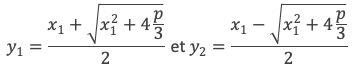
D’où :

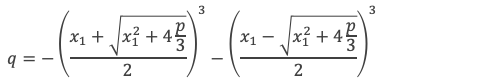
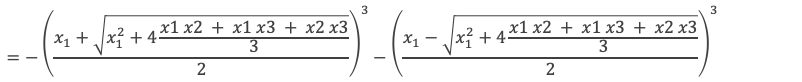
• Maintenant q² + 4(p/3)³ :

q² + 4(p/3)³ = x₁² (x₂ x₃)² + 4(p/3)³  = x₁² (p – x₁ x₂ – x₁ x₃)² + 4(p/3)³  = x₁² (p + x₁²)² + 4(p/3)³  = x₁⁶ + 2px₁⁴ + p²x₁²  + 4(p/3)³   =  x₁⁶ + 6(p/3)x₁⁴ +9 (p/3)²x₁²  + 4(p/3)³   = (x₁² + 4p/3)_*( x₁⁴ + 2 x₁²p/3 + (p/3)²) = (x₁² + 4p/3) )_*(x₁² + (p/3))²=  (y₁³ – y₂³)²

En effet :

(y₁³ – y₂³)² = (y₁ – y₂)²_*( y₁² + y₁y₂ + y₂²)² = (x₁²+4p/3)_*(2x₁²/4 + 2x₁²/4 + 2_*4p/3/4 + x₁²/4 – ( x₁²+4p/3)/4)² = (x₁²+4p/3)_*(x₁² + p/3)²

D’où :

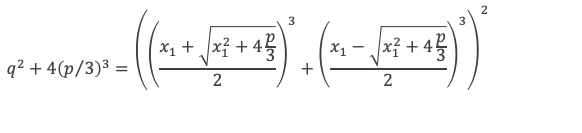
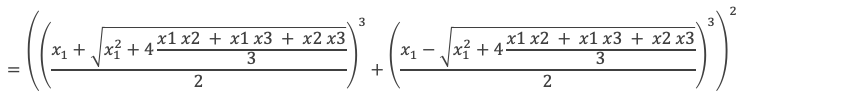
En reportant dans E les expressions de q et q² + 4(p/3)³ en fonction des racines, on a :

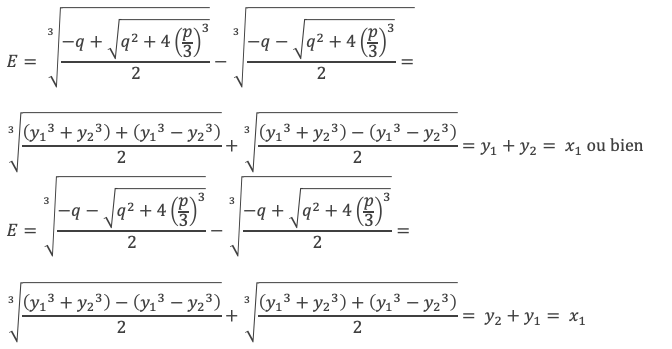
L’expression de départ exprimée avec les termes symétriques p et q s’est finalement simplifiée pour se réduire à x₁.