Enoncé

Le problème de la quadrature du cercle consiste à construire, à l’aide seulement d’une règle et d’un compas, un carré qui aurait la même aire que celle d’un disque donné (cf figure 1).

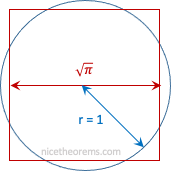
La démonstration repose sur le fait que la quadrature du cercle nécessiterait la construction à la règle et au compas de √π. Or les nombres qui sont construits à l’aide de la règle et du compas sont tous forcément solutions d’une équation polynomiale particulière (on dit de ces nombres qu’ils sont algébriques). La racine carrée du nombre π ne peut pas , elle, être la solution d’une telle équation, elle ne fait pas partie des nombres algébriques.

Histoire du théorème

La quadrature du cercle était l’un des trois grands problèmes de l’Antiquité, avec la trisection de l’angle et la duplication du cube, et a été celui qui a résisté le plus longtemps. Il a fallu plus de 3 millénaires pour finalement établir définitivement qu’il était insoluble, preuve apportée en 1882 par Ferdinand Lindemann.

Vers 1650 av. J.C. le scribe Ahmes rédige le papyrus de Rhind, En introduction du texte il indique qu’il s’agit de la copie d’une version précédente datant d’un pharaon qui vivait près de trois siècles auparavant. Dans les problèmes 48 et 50 de ce papyrus, le scribe étudie le rapport liant l’aire d’un disque à son diamètre en cherchant à ramener l’aire de la circonférence à celle d’un carré équivalent. Le papyrus Rhind précise ainsi une première approche de la quadrature du cercle : le carré de côté 8 unités a la même surface qu’un cercle de diamètre 9. Cette approximation se traduirait dans nos notations actuelles pour la surface d’un disque et d’un carré par : π×(9/2)2≃82. Ce qui correspond à une valeur de  π = 3,16 .

Vers 430 av. J.C Le philosophe Anaxagore aurait énoncé (ou dessiné) la quadrature du cercle. C’est l’écrivain grec Plutarque  qui le rapporte, mais il ne dit rien de plus sur la construction d’Anaxagore.

Archimède (Syracuse, 287 – ca 212 av. J.C.), dans son traité intitulé De la mesure du cercle  démontre que le rapport du périmètre au diamètre du cercle est compris entre 3 + 10⁄71 et 3 + 10⁄70. A partir de ce résultat Archimède fournit une valeur (22/7) à la fois simple et suffisamment précise (≈ 3,143) pour les applications courantes.

Au moyen age l’approximation de π par 22/7 proposée par Archimède était considéré comme exacte, et la question de la quadrature du cercle ne se posait donc plus.

Ce n’est qu’avec la diffusion des traductions en latin des traités d’Archimède, au Moyen Âge tardif, que l’on réalisa que 22/7 n’était qu’une valeur approchée et que des penseurs, comme Nicolas de Cues, se remirent à la quadrature du cercle.

Au 16^e siècle, Oronce Fine et Joseph Juste Scaliger croient avoir démontré la quadrature, mais Adrien Romain et le chevalier Errard de Bar le duc le contestent. Dans cette polémique, François Viète la décrète impossible. Le problème dépasse la sphère des mathématiques et l’on voit surgir des allusions à la quadrature dans des ouvrages ésotériques. Au 17^e siècle, Grégoire de Saint-Vincent crut avoir résolu l’énigme de la quadrature et exposa ses solutions dans un ouvrage de 1 000 pages.

A partir du 18^e siècle les recherches d’amateurs se multiplient. S’appuyant tantôt sur une construction mécanique, numérique ou une formule d’encadrement, les chercheurs prétendent qu’ils résolvent « exactement » le problème. Les communications sur ce sujet parvenaient en si grand nombre aux sociétés savantes que l’Académie des sciences de Paris décida dès 1775 de ne plus expertiser désormais ce genre de travaux : « L’Académie a pris, cette année, la résolution de ne plus examiner aucune solution des problèmes de la duplication du cube, de la trisection de l’angle ou de la quadrature du cercle, ni aucune machine annoncée comme un mouvement perpétuel. »

Même la démonstration d’impossibilité de Lindemann ne mit pas un terme à la profusion de prétendues solutions au problème.

Pour résoudre la quadrature du cercle, il fallait d’une part traduire la notion de « constructibilité géométrique » en une propriété algébrique, et d’autre part approfondir la compréhension que l’on avait des propriétés du nombre π.

Toute construction à la règle et au compas s’appuie sur un nombre fini de points donnés et consiste à construire en un nombre fini d’étapes de nouveaux points par intersection de deux droites, de deux cercles, ou d’une droite et d’un cercle. La traduction de ce procédé en langage algébrique s’opère par l’emploi d’un système de coordonnées, qui est l’idée fondamentale de la géométrie analytique imaginée au 17^e siècle par Pierre de Fermat et René Descartes. Avec un tel système, il est possible de raisonner sur les droites et cercles par leurs équations : les points d’intersection à construire deviennent les solutions d’équations algébriques à calculer. On trouve ainsi que les segments exactement constructibles à la règle et au compas ne sont autres que les nombres obtenus à partir de l’unité par un nombre fini d’opérations arithmétiques (addition, soustraction, multiplication et division) et d’extractions de racines carrées. En particulier, un tel nombre est algébrique, c’est-à-dire solution d’une équation algébrique de degré arbitraire à coefficients rationnels. Les nombres non algébriques sont dits transcendants et ne sont pas constructibles.

C’est en 1837 que Pierre-Laurent Wantzel démontre un théorème qui permet d’exhiber la forme des équations dont sont solutions les nombres constructibles à la règle et au compas : les nombres constructibles sont les nombres rationnels et les racines de certains polynômes de degré 2ⁿ à coefficients entiers (plus précisément les éléments d’une tour d’extensions quadratiques) ; les nombres constructibles font donc partie de l’ensemble des nombres algébriques (qui sont les racines de polynômes de degré fini quelconque à coefficients entiers).

Ferdinand von Lindemann parvint finalement à démontrer en 1882 que π n’est pas algébrique, autrement dit qu’il est transcendant ; qu’en conséquence, on ne peut construire à la règle et au compas un segment de longueur π et donc, que la quadrature du cercle est impossible.

Lindemann s’appuya pour cela sur un résultat du mathématicien français Charles Hermite. Ce dernier avait démontré en 1873 que le nombre e est transcendant

Boîte à outils

1. Points constructibles :

Qu’entend-on par construire un point, une droite, un cercle, un carré, un nombre ? Le concept mathématique de « construction » peut être fondé sur une définition par récurrence :

– le point O et le point I situé à une distance unité de 0, sont des points constructibles. Ils constituent les 2 points de départ de la construction.

– une droite est constructible si et seulement si elle passe par deux points constructibles.

– un cercle est constructible si et seulement si son centre est un point constructible et son rayon est la distance entre deux points constructibles.

– tout point du plan est un point constructible si il est intersection de deux ensembles de points constructibles (droite ou cercle)

Autrement dit, si E désigne un ensemble fini de points du plan, on considère l’ensemble P des droites joignant deux de ces points, ainsi que des cercles centrés en l’un de ces points et de rayon la distance entre deux de ces points. On appelle « points construits à partir de E à la règle et au compas » l’ensemble des intersections des éléments de P.

Un point M du plan est alors dit « constructible » s’il existe une suite de points M₁, M₂, … , M_n avec M_n = M telle que pour tout i < n, M_i soit un point construit à partir de l’ensemble {O, I,M₁, . . . ,M_i−1}.

Un réel x est dit « constructible » s’il est l’abscisse ou l’ordonnée d’un point constructible. De manière équivalente, x est constructible s’il est l’abscisse d’un point constructible de l’axe (OI). En effet, si M est constructible, alors le cercle de centre O passant par l’ordonnée de M coupe l’axe des abscisses en un point qui devient constructible. L’axe OI contient l’ensemble des coordonnées des points constructibles (abscisses et ordonnées).

2. Exemples de constructions :

– Construction d’un repère orthonormé O, I, J à partir des points de départ O et I: pour cela on construit le point K symétrique de I par rapport à O (intersection de la droite (OI) et du cercle C de centre O et de rayon OI). 

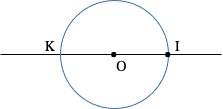
Ensuite, à partir des intersections A et B des 2 cercles de même rayon, l’un centré sur O l’autre sur I,  l’axe (OJ) comme médiatrice du segment [IK]. 

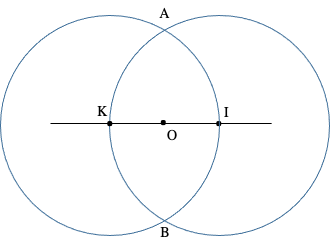
Le point J est alors intersection de cet axe avec le premier cercle de rayon OI déjà construit.

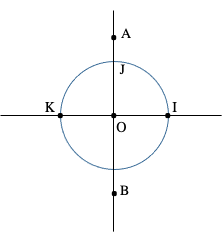
– Construction d’une droite parallèle à une droite (AB) et passant par un point C : On construit le quatrième point D du parallélogramme ABCD en traçant un arc de cercle de centre C et de rayon AB, et un arc de cercle de centre B et de rayon AC.

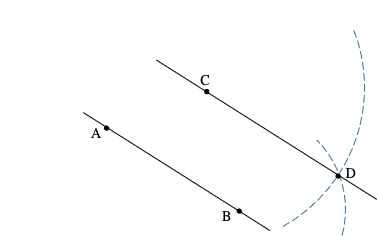
– Si a et b sont deux nombres constructibles, il en est de même pour leur somme, ou de leur différence :

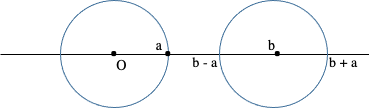
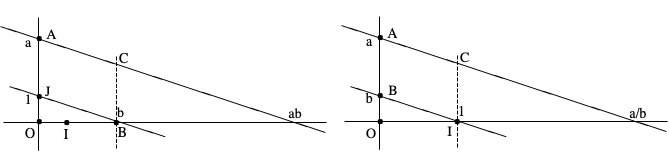
– Si a et b sont 2 nombres constructibles, il en est de même pour leur produit ou leur rapport (or cas du point 0 évidemment). 

Nous avons vu précédemment comment construire une parallèle à une droite donnée passant par un point donné. Pour l’obtention du produit ab, on construit le quatrième sommet C du parallélogramme de sommets A(0, a), J (0, 1) et B(b, 0). Grâce au théorème de Thales, ab est donné par l’intersection de la droite AC avec l’axe OI. Pour l’obtention du rapport a/b, on construit le quatrième sommet C du parallélogramme de sommets A(0, a), B (0, b) et I(1, 0). Grâce au théorème de Thales, a/b est donné par l’intersection de la droite AC avec l’axe OI. 

– Construction de la racine carrée d’un nombre a. La figure suivante montre comment le point M construit à partir du cercle C de diamètre a + 1  et de centre (a-1)/2 a pour ordonnée √a. En effet comme M est sur le cercle C, le triangle qu’il forme avec les points K d’abscisse −1 et A d’abscisse a est rectangle en M. Les triangles AOM et KOM sont donc semblable, et l’on obtient :

OK / OM = OM / OA, soit OM² = a

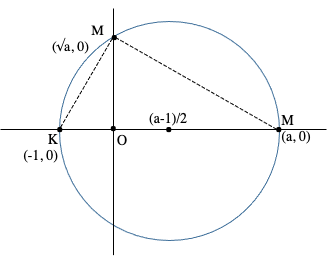
On voit qu’avec les procédés présentés on peut contruire, à partir de nombres rationnels, des nombres assez élaborés, par exemple de la forme :

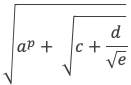
3. La croissance de (p-1)! est supérieure à celle de x^p :

Pour tout x on a, à partir d’un certain rang, c’est-à-dire pour tout entier supérieur à p₀ : (p-1)! > x^p

Démonstration : 

Le résultat est trivial pour x ≤ 1, on s’intéresse donc à x > 1 et on note h = arrondi de x à sa valeur supérieure + 1 ce qui garantit h > x. Prenons p₀ = 2_*h²+ 1. 

(p₀-1)! = (p₀-1)_*(p₀-1-1) … (p₀-1 – (p₀-1)/2 )_*( p₀-1 – (p₀-1)/2-1) …  _*3_*2_*1

Chacun des termes (p₀ – k) avec k ≤ (p₀-1)/2 est ≥ (p₀-1)/2 = h², et il y en a (p₀-1)/2 + 1= (p₀+1)/2

Nous avons donc : 

(p₀-1)! ≥ (h²) ^(p₀+1)/2_* ( p₀-1 – (p₀-1)/2-1) …  _*3_*2_*1 ≥ h^p₀+1_*3_*2_*1 > x^p₀

Et pour tout p > p0 : p = p₀ + i avec i ≥ 1 :

(p-1)! = (p-1)_*(p-2) … (p – (i-1))_*(p-i)_*(p₀-1) ! > (p-1)_*(p-2) … (p – (i-1))_*(p-i) x^p₀

Dans ce produit tous les termes (p-1) jusqu’à (p–i) sont ≥ p₀ et p₀ lui-même est > x , donc :

(p-1)! > xⁱ_*x^p₀ = x^p

4. Les polynomes symétriques :

4-1 Définition : Un polynôme Q(a₁, …, a_n) en n indéterminées est dit symétrique si pour toute permutation s de l’ensemble d’indices {1, …, n}, l’égalité suivante est vérifiée :

Q(a₁, …, a_n) = Q(a_s(1), …, a_s(n))

Par exemple : 

• Pour n = 2 : le polynôme a₁ + a₂ est symétrique alors que le polynôme a₁ + a₂² ne l’est pas.
• Pour n = 3 : les polynômes a₁a₂a₃ ou (a₁ – a₂)²(a₁ – a₃)²(a₂ – a₃)² sont symétriques.

Polynômes symétriques élémentaires : On appelle polynôme symétrique élémentaire en n variables les polynômes qui sont la somme de tous les produits de k d’entre ces n variables. Nous notons PS_k(a₁, …, a_n) ces polynômes. Exemples de ce type de polynômes :

• PS₂(a₁, …, a_n) = Σa_ia_j  avec i et j compris entre 1 et n, et i < j.
  • Pour n = 3 : PS₂(a₁, a₂, a₃) = a₁ a₂ + a₁ a₃ + a₂ a₃
  • Pour n = 2 : PS₂(a₁, a₂) = a₁ a₂
• PS₃(a₁, …, a_n) = Σ a_i a_j a_k avec i, j, k compris entre 1 et n, et i < j < k.
  • Pour n = 3 : PS₃(a₁, a₂, a₃) = a₁ a₂ a₃
  • Pour n = 4 : PS₃(a₁, a₂, a₃, a₄) = a₁ a₂ a₃ + a₁ a₂ a₄ + a₁ a₃ a₄  + a₂ a₃ a₄
  • Pour n = 4 : PS₁(a₁, a₂, a₃, a₄) = a₁ + a₂ + a_{3 +} a₄

4-2 Propriété des polynomes symétriques :

Tout polynôme symétrique peut être exprimé comme une combinaison algébrique de polynômes symétriques élémentaires, et plus précisément sous la forme d’un polynôme dont les variables sont des polynômes symétriques élémentaires. Ce résultat joue un rôle clé pour faire aboutir les calculs détaillés en annexe.

Par exemple, considérons le polynôme symétrique Q suivant qui n’est pas élémentaire :

Q(a₁, a₂, a₃) = (a₁ + a₂)²(a₁ + a₃)²(a₂ + a₃)²

= ((a₁ + a₂)(a₁ + a₃)(a₂ + a₃))²

= ((a₁² + a₁a₃ + a₂a₁ + a₂a₃)(a₂ + a₃))² = (a₂a₁² + a₂a₁a₃ + a₂²a₁ + a₂²a₃ + a₃ a₁² + a₁a₃² + a₃a₂a₁ + a₂a₃²)²

On remarque que : a₂a₁² + a₂²a₁ + a₂²a₃ + a₃ a₁² + a₁a₃² + a₂a₃² = PS₁PS₂ -3PS₃

D’où 

Q(a₁, a₂, a₃) = (2PS₃ + PS₁PS₂ -3PS₃)² = (PS₁PS₂ -PS₃)² = (PS1PS2)² – 2 PS₁PS₂PS₃ + PS₃²

Démonstration :

Nous avons tout d’abord besoin d’introduire la notion de monômes d’un polynôme. Le développement d’un polynôme Q(a₁, a₂, a₃ … a_n), c’est-à-dire la suppression de toutes les factorisations, conduit à l’exprimer sous la forme d’une somme de termes de la forme A_*a₁^m₁ a₂^m₂ a₃^m₃ … a_n^m_n. où A est un coefficient. Ces termes sont appelés monômes. Par exemple :

Q(a₁, a₂, a₃) = a₁² (a₁ + a₂) – 5(a₁  + 2a₃)² = a₁³ + a₁²a₂ – 5 a₁² -10 a₁a₃ – 20a₃²

Les termes : a₁³, a₁²a₂, -5a₁², -10a₁a₃, et -20a₃² sont les monômes de Q. 

L’ensemble des exposants (m₁, m₂, m₃ …, m_n) des monômes A_*a₁^m₁ a₂^m₂ a₃^m₃ … a_n^m_n peut être ordonné suivant un ordre appelé l’ordre lexicographique. On écrira :

a₁^m₁ a₂^m₂ a₃^m₃ … a_n^m_n > a₁^p₁ a₂^p₂ a₃^p₃ … a_n^p_n si pour le premier i tel que m_i ≠ p_i, on a m_i > p_i. Par exemple, avec le polynôme Q précédent les exposants des monômes  sont (3,0,0) pour a₁³, (2,1,0) pour a₁²a₂ , (2,0,0) pour a₁², (1,0,1) pour a₁a₃, et (0,0,2) pour a₃². On écrira donc :

a₁³ > a₁²a₂ > a₁² > a₁a₃ > a₃²

Nous pouvons maintenant passer à la démonstration de la décomposition d’un polynôme symétrique en polynômes symétriques élémentaires.

Soit P(a₁, a₂, a₃ … a_n) un polynôme symétrique non nul, et A_*a₁^m₁ a₂^m₂ a₃^m₃ … a_n^m_n son monôme le plus grand (au sens de l’ordre lexico graphique défini auparavant. Procédons par récurrence  sur les ordres des monômes de P. Pour cela supposons que la propriété de décomposition d’un polynôme symétrique en polynômes symétriques élémentaires soit vraie pour tout polynôme symétrique dont le monôme le plus grand est strictement inférieur à a₁^m₁ a₂^m₂ a₃^m₃ … a_n^m_n. Alors nous allons voir qu’elle devient aussi vraie pour A_*a₁^m₁ a₂^m₂ a₃^m₃ … a_n^m_n.

Puisque P est symétrique, il contient, affectés d’un même coefficient non nul, tous les monômes obtenus en permutant les exposants dans le monôme le plus grand A_*a₁^m₁ a₂^m₂ a₃^m₃ … a_n^m_n.

Par exemple, pour n = 4,  si P est symétrique et contient le monômes 5a₁ a₂² a₃³ a₄⁴ alors il contient alors forcément 5a₂ a₁²a₃³ a₄⁴ , ou 5a₂ a₃² a₁³ a₄⁴ ou … 5a₁⁴ a₂³ a₃² a31 et son ordre le plus grand est au moins (4,3,2,1). 

D’une façon générale si le polynôme est symétrique et contient un monôme de la forme A_*a₁^p₁ a₂^p₂ a₃^p₃ … a_n^p_n alors il contiendra un monôme de la forme A_*a₁^m₁ a₂^m₂ a₃^m₃ … a_n^m_n construit à partir de a₁^p₁ a₂^p₂ a₃^p₃ … a_n^p_n en permutant les variables de ce monôme pour mettre le plus grand exposant sur a₁ puis le suivant sur a₂, puis etc. Cela permet d’affirmer que le monôme le plus grand A_*a₁^m₁ a₂^m₂ a₃^m₃ … a_n^m_n vérifie :

m₁ > m₂  > m₃ …  > m_n

Posons r_i = m_i – m_i+1 pour 1 ≤ i < n, et r_n = m_n. Les r_i sont tous positifs ou nuls. 

Considérons le polynôme symétrique R(a1, a2, a3 … an) = A*PS1r1* PS2r2* PS3r3* … * PSnrn

Notons bien que le monôme maximal de PS₁ est a₁, le monôme maximal de PS₂ est a₁a₂, le monôme maximal de PS₃ est a₁a₂a₃, …etc, et le monôme maximal de PS_n est a₁a₂a₃, … a_n. Etudions les exposants de a₁, a₂, a₃ … a_n dans le monôme d’ordre maximal de R :

• L’exposant de a₁ est donné par : a₁^r₁a₁^r₂a₁^r₃ … a₁^r_m = a₁^m₁–m₂a₁^m₂–m₃a₁^m₃–m₄ … a₁^m_n-1–m_na₁^m_m = a₁^m₁
• L’exposant de a₂ est donné par : a₂^r₂a₂^r₃ … a₂^r_m = a₂^m₂–m₃a₂^m₃–m₄ … a₂^r_m = a₂^m₂
• L’exposant de a₃ est donné par : a₃^r₃ … a₃^r_m = a₃^m₃–m₄ … a₃^r_m = a₃^m₃
• …
• L’exposant de a_n est donné par : a_n^r_m

P et R ont donc le même monôme maximal et donc le polynôme symétrique P – R est nul ou a un monôme  maximal strictement inférieur à celui de P. 

Si P – R est nul, alors cela signifie que P = R : il est donc bien construit à partir des polynômes symétriques élémentaires.

Si P – R n’est pas nul, alors le polynôme W = P – R est un polynôme symétrique d’ordre maximal strictement inférieur à a₁^m₁ a₂^m₂ a₃^m₃ … a_n^m_n  , il est donc par hypothèse de la récurrence construit à partir des polynômes symétriques élémentaires, et donc P = W + R  l’est aussi.

Ce raisonnement, appliqué de proche en proche à la succession ordonnée des monômes maximaux des polynômes symétriques permet de conclure qu’un polynôme symétrique peut toujours être décomposé en polynômes symétriques élémentaires.

Les éléments clés de la démonstration

1^ère étape :

Nous montrerons que les nombres qui sont construits à l’aide de la règle et du compas sont forcément solutions d’une équation polynomiale à coefficients rationnels. C’est à dire une équation de la forme : 

a₀ + a₁x + a₂x² + … a_kx^k + … + a_m x^m  = 0,  avec m entier et qi nombres rationnels.

2ème étape : 

Dans un premier temps nous montrerons que π ne peut pas être solution d’une équation polynomiale à coefficients rationnels. C’est dans cette partie que réside l’essentiel de la difficulté. La démarche qui va permettre de le démontrer se décompose en 3 phases :

1- Nous faisons l’hypothèse que π est solution d’une équation polynomiale à coefficients rationnels. Cela signifie qu’il existe un polynôme noté T(x) tel que T(π) = 0 . En travaillant un peu ce polynôme nous le ramènerons à un polynôme P(x) n’ayant que des coefficients en nombre entiers, et tel que P(i π) = 0 , avec i imaginaire racine de -1.

2- A partir des racines de ce polynôme à coefficients entiers nous allons construire un autre polynôme, plus complexe, de degré plus élevé, qui sera noté F(x). Ce polynôme permet de créer un nombre J qui aurait d’étranges propriétés.

3- Les propriétés sont si étranges qu’elles donnent des résultats contradictoires. J est forcément supérieur à nombre J1 et en même temps J est forcément inférieur à un nombre J2 tout cela avec J2 supérieur à J1. Ces résultats contradictoires prouvent que ce polynôme ne peut pas exister, et que donc l’hypothèse de départ qui dit que π est constructible (donc algébrique) est fausse. En fait π est transcendant.

Il est alors très simple de montrer que π étant non constructible et même transcendant, √π l’est aussi forcément. Un carré d’aire identique à un cercle de rayon 1, c’est à dire un carré d’aire π et donc de côté √π n’est pas constructible à la règle et au compas.

Démonstration de l’impossibilité de la quadrature du cercle

Etape 1: il s’agit de montrer que si un nombre est constructible alors il est solution d’une équation polynomiale à coefficients rationnels.

Soit M un point constructible. Il existe une suite de points du plan M₁, M₂, … , M_n avec M_n = M telle que pour tout i ≤ n, M_i soit un point construit à partir de l’ensemble des points {O, I, M₁, . . , M_i−1}. 

A chaque point M_i on va associer l’ensemble K_i de tous les nombres réels que l’on peut former par addition, soustraction, multiplication, division, à partir des coordonnées des points M_i, M_i-1, … M₂, M₁, I, O. Par exemple, à partir des points de départ O et I on peut générer de cette façon l’ensemble K₀ = Q ensemble des nombres rationnels. A la succession des points M_i est ainsi associé une succession d’ensembles K_i telle que K_i ⊆ K_i+1.

Les coordonnées de M = M_n sont par définition dans K_n.

Tout point M_i est construit à partir des points précédents M1,M2, … , M_i-1, c’est-à-dire qu’il est l’intersection soit :

• de 2 droites passant chacune par 2 de ces M_i-1 points,
• d’une droite passant par 2 de ces M_i-1 points et d’un cercle centré en l’un de ces M_i-1 points et de rayon la distance entre deux de ces M_i-1 points.
• de 2 cercles centrés chacun en l’un de ces M_i-1 points et ayant pour rayon la distance entre deux de ces M_i-1 points.

Lemme 1: Les coordonnées de M_i (x_i, y_i) étant dans K_i, ces coordonnées sont soit déjà dans K_i-1, soit solutions d’une équation polynomiale de degré 2 à coefficients dans K_i-1. En effet :

1) Cas de l’intersection de 2 droites : on pose P₁(a₁, b₁) et R₁(c₁, d₁) les points définissant la première droite, et P₂(a₂, b₂) et R₂(c₂, d₂) les points définissant la seconde. Les coordonnées a, b, c, d sont dans K_i-1.

L’équation de la première droite est : Y = (d₁ – b₁) / (c₁ – a₁) (X – a₁) + b₁

L’équation de la seconde droite est : Y = (d₂ – b₂) / (c₂ – a₂) (X – a₂) + b₂

Le point d’intersection entre les 2 droites est solution d’un système de 2 équations à 2 inconnues, dont les coefficients sont dans K_i-1. Le résultat est issu d’additions, soustractions, multiplications sur ces coefficients, il sera forcément dans K_i-1.

On est dans le cas où les coordonnées de M_i (l’abscisse comme l’ordonnée) sont déjà dans K_i-1, c’est-à-dire que K_i = K_i-1.

2) Cas de l’intersection d’une droite et d’un cercle : On pose P₁(a₁, b₁) et R₁(c₁, d₁) les 2 points définissant la droite, P₂(a₂, b₂) le centre du cercle, et r son rayon. a₁, b₁, c₁, d₁, a₂, b₂, et r sont donc dans K_i-1.

L’équation de la droite est. : Y = (d₁ – b₁) / (c₁ – a₁) (X – a₁) + b_1. (1)

L’équation du cercle est : (X – a₂)² + (Y – b₂)² = r.      (2)

En remplaçant Y par (d₁ – b₁) / (c₁ – a₁) (X – a₁) + b₁ dans l’équation (2) du cercle, on en déduit que X est solution de (X – a₂)² + [(X – a₁)(d₁ – b₁) / (c₁ – a₁) + b₁ – b₂]² = r. Donc X est solution d’une équation de degré 2 dont les coefficients sont dans K_i-1. X s’écrira sous la forme X = A_x + B_x√D avec A_x, B_x, et D appartenant à K_i-1. De même Y est solution d’une équation de degré 2, et en vertu de (1) Y s’écrit sous une forme identique à X à savoir Y = A_y + B_y√D avec A_y, B_y, et D appartenant à K_i-1. On notera que l’extension en √D est la même pour X et Y.

3) Cas de l’intersection de 2 cercles : On pose P₁(a₁, b₁), P₂(a₂, b₂) les centres des 2 cercles, et r₁respectivement r₂ les rayons. a₁, b₁, a₂, b₂, r₁, r₂,  sont dans K_i-1.

L’équation du premier cercle est. : (X – a₁)² + (Y – b₁)² = r₁  (1)

L’équation du second cercle est : (X – a₂)² + (Y – b₂)² = r_2.    (2)

En soustrayant (2) à (1), le système d’équation équivalent s’écrit :

(X – a₁)² – (X – a₂)² + (Y – b₁)² – (Y – b₂)² = r₁ – r₂

(X – a₂)² + (Y – b₂)² = r_2. 

⟺

-2X(a₁ – a₂) -2Y(b₁ – b₂) + a₁² – a₂² + b₁² – b₂² = r₁ – r₂

(X – a₂)² + (Y – b₂)² = r_2. 

On retrouve un système d’équation du même type que lors de l’intersection d’une droite et d’un cercle. La conclusion sera la même : X et Y sont chacun solution d’une équation de degré 2 dont les coefficients sont dans K_i-1 et X et Y s’écrivent sous la même forme A_x + B_x√D pour X et A_y + B_y√D pour Y avec A_x, B_x, D, A_yet B_y appartenant à K_i-1.

Le lemme 1 est démontré.

La conséquence du lemme 1 est que pour tout x de K_i, soit x appartient à K_i-1 (si K_i = K_i-1 c’est-à-dire que M_i est construit par l’intersection de 2 droites), soit x s’exprime sous la forme x = x₁ +x₂√∆_i avec x₁, x₂ et ∆_i appartenant à K_i-1. En effet si M_i est construit comme l’intersection d’une droite et d’un cercle, ou de 2 cercles, alors les coordonnées de M_i (l’abscisse, comme l’ordonnée) auront tous les deux la même forme avec une extension en √∆_i. Donc tous les nombres générés à partir des coordonnées de M_i soit par addition, soustraction, multiplication, division auront aussi cette forme car :

• (x₁ + x₂√∆_i) +/- (y₁ + y₂√∆_i) = (x₁ + y₁) +/- (x₂ + y₂)√∆_i)
• (x₁ + x₂√∆_i) _* (y₁ + y₂√∆_i) = [(x_1*y₁ + x_2*y₂∆_i)+ (x_1*y₂ + x_2*y₁)√∆_i]
• (x₁ + x₂√∆_i) / (y₁ + y₂√∆_i) = (x₁ +  x₂√∆_i) ((y₁ – y₂√∆_i) / (y₁ + y₂√∆_i) ((y₁ – y₂√∆_i) = (x₁ + x₂√∆_i) ((y₁– y₂√∆_i) / (y₁² – y₂²∆_i) = [(x_1*y₁ – x_2*y₂ ∆_i) + (-x_1*y₂ + x_2*y₁)√∆_i] / (y₁² – y₂²∆_i)

Lemme 2: soit K_i l’ensemble associé à M_i et K_i-1 associé à M_i-1. Si x est solution d’une équation polynomiale de degré p à coefficients dans K_i, alors x est solution d’une équation polynomiale de degré p ou 2p à coefficients dans K_i-1.

Démonstration : nous supposons donc que x est solution de l’équation :

P(X) = a₁ + a₂ X + a₃X² +… + a_p-1 X^p-1 + a_p X^p = 0, avec a₁, a₂, … , a_p-1 , a_p coefficients dans K_i. et a_p non nul.

Si K_i = K_i-1 nous sommes dans le cas trivial où le lemme est vrai et l’équation a pour degré p.

Si K_i ≠ K_i-1  tous les a_i s’écrivent sous la forme : a_i = a_i1 + b_i2 √∆_i avec a_i1, b_i2, et ∆_i ϵ K_i-1. En remplaçant les a_i par a_i1 + b_i2 √∆_i dans l’équation P(X) = 0 on obtient : P₁(X) + P₂(X) *√∆_i = 0 avec P₁(X) et P₂(X) deux polynômes de degré p (au moins pour l’un d’entre eux) et à coefficients dans K_i-1. D’où :

P₁(X)² – P₂(X)²∆_i = 0 

x est solution de ce polynôme dont tous les coefficients appartiennent à K_i-1 et qui est de degré 2p (le terme de degré 2p s’écrit a_p1² – b_p1²∆_i qui ne peut s’annuler que si a_p1 = b_p1 √∆_i puisque a_p est non nul, et a_p1 = b_p1 √∆_i signifierait que √∆_i appartient à K_i-1 et que donc K_i = K_i-1 ce qui ne correspond pas à l’hypothèse).

Revenons maintenant au point M = M_n, et à la suite des points M₁, M₂, … , M_n-1 qui ont permis de le construire. A cette succession de points est associée la succession des ensembles K₀, K₁, K₂, … , K_n-1. 

D’après le lemme 1, comme le point M est constructible, ses coordonnées sont soit dans M_n-1, soit solutions d’une équation de degré 2 à coefficients dans M_n-1. 

Par le lemme 2 on en déduit que ses coordonnées sont soit dans M_n-2 soit solutions d’une équation de degré 2 ou 2*2 à coefficients dans M_n-2, puis de nouveau par le lemme 2 ses coordonnées sont soit dans M_n-3 soit solutions d’une équation de degré 2 ou 2*2 ou 2³ à coefficients dans M_n-3 et ainsi de suite juste qu’à descendre par le lemme 2 au point M₁ puis au point I qui correspond à K₀ = Q = ensemble des rationnels. Cela qui permet de conclure que les coordonnées de M = M_n sont solutions d’une équation polynomiale de degré < 2n à coefficients dans Q.

Etape 2: il s’agit maintenant de démontrer que π (ou sa racine) n’est pas solution d’une équation polynomiale à coefficients rationnels

La démarche pour ce faire se décompose en 3 phases :

1- Nous faisons l’hypothèse que π est solution d’une équation polynomiale à coefficients rationnels. Cela signifie qu’il existe un polynôme noté T(x) tel que T(π) = 0 . En travaillant un peu ce polynôme nous le ramènerons à un polynôme P(x) n’ayant que des coefficients en nombre entiers, et tel que P(i π) = 0 , avec i imaginaire racine de -1.

2- A partir des racines de ce polynôme à coefficients entiers nous allons construire un autre polynôme, plus complexe, de degré plus élevé, qui sera noté F(x). Ce polynôme permet de créer un nombre J qui aurait d’étranges propriétés.

3- Les propriétés sont si étranges qu’elles donnent des résultats contradictoires. J est forcément supérieur à nombre J1 et en même temps J est forcément inférieur à un nombre J2 tout cela avec J2 supérieur à J1. Ces résultats contradictoires prouvent que ce polynôme ne peut pas exister, et que donc l’hypothèse de la phase 1 est fausse.

Commençons par la première phase de la démarche :

Hypothèse : π est solution d’une équation polynomiale à coefficients rationnels. On note T(x) ce polynôme, supposé de degré m.

T(x) = t₀ + t₁x + t₂x² + … t_kx^k + … + t_mx^m ,  et on a T(π) = 0

Les t_k sont des coefficients rationnels, donc de la forme p_k/b_k avec p_k et b_k des entiers relatifs.

π sera alors aussi solution d’une équation polynomiale à coefficients entiers ; il suffit pour l’obtenir de multiplier l’équation de départ par le produit des dénominateurs des coefficients, c’est-à-dire le produit des b_k. On note T1(X) ce polynôme à coefficients entier, et c_k les coefficients entiers de ce polynôme.

T1(x) = c₀ + c₁x + c₂x² + … c_kx^k + … + c_m x^m ,  et on a T1(π) = 0

Le nombre (i π) pourra lui aussi être solution d’une équation polynomiale à coefficients entier. Pour la construire on part du polynôme T1(x) dans lequel on réarrange chaque monome  c_k x^k  sous la forme c_k/(i) ^k * (i x)^k.

Le nouveau polynôme T2(x) avec ses coefficients de la forme c_k/(i) ^k vérifie T2(i π) = 0

Comme 1/(i) ^k  = 1 ou -1 ou i ou –i, les coefficients de T2(x) sont de la forme c_k ou – c_k ou i c_k ou –i c_k avec c_k  nombre entier. Réarrangeons maintenant T2(x) en séparant d’un côté les termes à coefficient purement entier (les +/- c_k), et de l’autre ceux qui sont le produit de i par un entier (les +/- i c_k) : 

T2(x) = T2r(x) + i T2im(x) où cette fois les coefficients de T2r et T2im sont tous des entiers purs.

On considère le polynôme P(X) défini par :

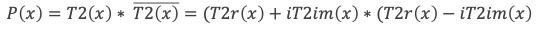
Le premier terme de ce produit est le polynôme T2(x), donc P(i π)  = 0

Et l’on a par ailleurs, en développant le produit  : P(x) = [T2r(x)]² +  [T2im(x)]² qui est un polynôme à coefficients purement entiers.

On dispose donc maintenant, comme annoncé pour l’étape 1, d’un polynôme P(x) à coefficients purement entiers et tel que P(i π)  = 0 

Nous notons pour la suite d le degré de ce polynôme, et son développement :

P(x) = s₀ + s₁x + s₂x² + … s_kx^k + … + s_d x^d avec les s_k entiers 

Ce polynôme possède d racines, dont une au moins vaut (i π). Nous noterons q₁, q₂, q₃, … q_d ces d racines, et considérerons que q₁ = i π  

Passons à la deuxième phase de la démarche :

Construction à partir de P(x) d’un polynôme étrange.

Nous partons du polynôme P(x) = s₀ + s₁x + s₂x² + … s_kx^k + … + s_d x^d avec les s_k entiers.  Nous savons que l’on a P(i π) = 0, et les racines de ce polynôme sont notées q_i.

On sait qu’avec la fonction exponentielle e, e ^{i π} = -1  donc  1 + e^q₁ = 0  et donc  (1 + e^q₁) (1 + e^q₂) ( 1 + e^q₃) …(1 + e^q_d) = 0

Développons ce produit, et pour faciliter la compréhension faisons le pour le cas particulier où d = 5

(1 + e^q₁) (1 + e^q₂) (1 + e^q₃) (1 + e^q₄) (1 + e^q₅) = 

1 +  e^q₁ + e^q₂ + e^q₃ + e^q₄  + e^q₅ (c’est-à-dire le produit des cinq 1 plus les produits de un terme e^q_k avec quatre 1, il y en a 5 au total)

+  toutes les combinaisons e^q_k+q_j  (c’est-à-dire les produits de 2 termes e^q_k avec trois 1, il y en a 10 au total)

+  toutes les combinaisons e^q_k+q_i+q_j  (c’est-à-dire les produits de 3 termes e^q_k avec deux 1, il y en a 10 au total)

+  toutes les combinaisons e^{q_k+q_i+q_j+q_p}  (c’est-à-dire les produits de 4 termes e^q_k avec un 1, il y en a 5 au total)

+ e^{q₁+q₂+q₃+q₄+q₅}

En final le produit développé est la somme de tous les termes possibles de la forme e^{ε₁.q₁+ε₂.q₂+ε₃.q₃+ε₄.q₄+ε₅.q₅} avec ε₁, ε₂, ε₃, ε₄, ε₅ prenant les valeurs 0 ou 1 indépendamment les uns des autres, ce qui donne 2⁵ possibilités et au total la somme est bien composée de 2⁵ termes, soit 32 termes.

Parmi ces 32 termes il y ceux pour lesquels ε₁.q₁ + ε₂.q₂  + ε₃.q₃ + ε₄.q₄ + ε₅.q₅ = 0 et qui donnent donc des 1 avec l’exponentiel (il y en a au moins un c’est le terme q₁), et ceux pour lesquels l’exposant est non nul et qui peuvent s’écrire, avec l’exponentiel : e^a_k avec a_k non nul.

Revenons maintenant à notre produit de départ :

(1 + e^q₁) (1 + e^q₂) (1 + e^q₃) (1 + e^q₄) (1 + e^q₅) = 0, et d’après ce qui précède cette équation peut être ré-écrite en :

N + e^a1 + e^a2 + e^a3 + e^{a4  + …. +} + e^a_n-1 + e^a_n  = 0, avec n = nombre de termes à exposant non nul et N = nombre total de termes à exposant nul = nombre total de termes moins ceux à exposant non nul = 2⁵ – n ≥ 1 car nous savons que le terme e^q₁ a un exposant nul.

D’où l’équation dans sa forme finale :  2⁵ – n + e^a₁ + e^a₂ + e^a₃ + e^a₄  + …. +  e^a_n-1 + e^a_n = 0

Par le même raisonnement, quel que soit le degré d de P(X) on construira l’équation 

2^d – n + e^a₁ + e^a₂ + e^a₃ + e^a₄  + …. +  e^a_n-1 + e^a_n = 0. (2-1)

avec a_i non nul = ε₁.q₁ + ε₂.q₂ + ε₃.q₃ + … + ε_k. q_k + … + ε_d-1.q_d-1 + ε_d.q_d , les ε_k valant 0 ou 1, et avec (2^d – n) ≥1. Notons au passage que parmi les a_i il y a q₁, q₂, … q_d, c’est à dire les d racine du polynôme P(X). Sans que cela restreigne la généralité de la démonstration nous pouvons convenir de nommer a_i = q₁, a₂ = q₂, a₃ = q₃, … a_d = q_d, puis a_d+1 = q₁ + q₂, a_d+2 = q₁ + q₃, … , a_d+j = une première somme de j parmi les d racines, … , a_n = q₁ + q₂ + q₃ + … + q_d

Nous voilà maintenant enfin en mesure de définir le polynôme étrange f(x). Ce polynôme s’écrit, par définition : 

f(x) = s_d^np x^p-1 (x – a₁)^p (x – a₂)^p … (x – a_n)^p avec p nombre premier qui sera judicieusement choisi plus tard.

Le degré m de f(x) est donné par: m = p – 1 + np = p(n + 1) – 1

Troisième et dernière phase: le polynôme f(x) ne peut pas exister

f(x) a été spécialement construit pour que ses dérivées successives en 0, notées f^(j)(0), soient toujours nulles, jusqu’à la dérivée (p-2)^ième, la (p-1)^ième et les suivantes ne le sont pas. De même ses dérivées successives en a_i sont toujours nulles, jusqu’à la dérivée (p-1)^ième, la p^ième et les suivantes ne le sont pas. 

Plus précisément, nous avons (le détail des laborieuses démonstrations qui le prouvent est donné en annexe) :

• (3-1) Pour k < p-1, f^(k)(0) = 0
• (3-2) Pour k = p-1, f^(p-1)(0) est entier, multiple de (p-1)!
• (3-3) Pour k > p-1, f^(k)(0) est entier, multiple de p!

Et aussi, pour tout a_i :

• (3-4) Pour k < p, f^(k)(a_i) = 0
• (3-5) Pour k ≥ p, Σ _i=1ⁱ⁼ⁿ f^(k)(a_i) est entier, multiple de p!

Ayant ces résultats en tête, calculons J défini par l’équation (3-0) suivante :

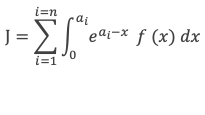
Et pour cela commençons par examiner le terme générique = intégrale de 0 à a_i de e^a_i–x f(x) dx, en effectuant une première intégration par partie :

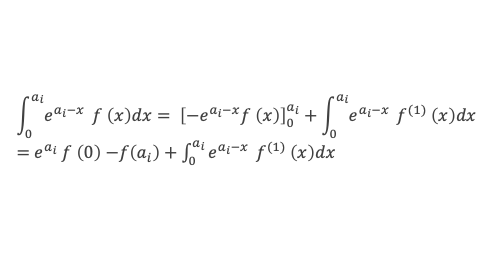
Appliquons le même calcul d’intégration par partie, cette fois à f⁽¹⁾(x), on obtiendra :

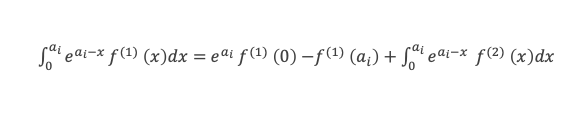
Et ainsi de suite pour f⁽²⁾(x), f⁽³⁾(x), etc … Au rang k on aura :

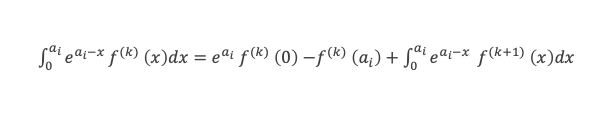
Et au rang m, sachant que f^(m+1)(x) = 0 puisque f(x) est un polynôme de degré m :

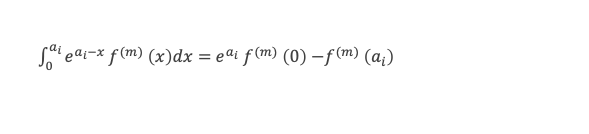
Et au rang m+1

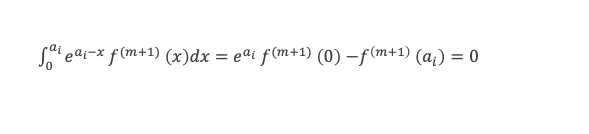
En faisant maintenant la somme de toutes les intégrations par partie que l’on vient de calculer, on obtient :

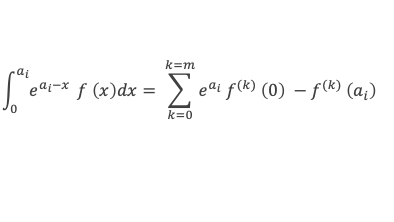
Ce qui permet de ré-écrire J sous la forme :

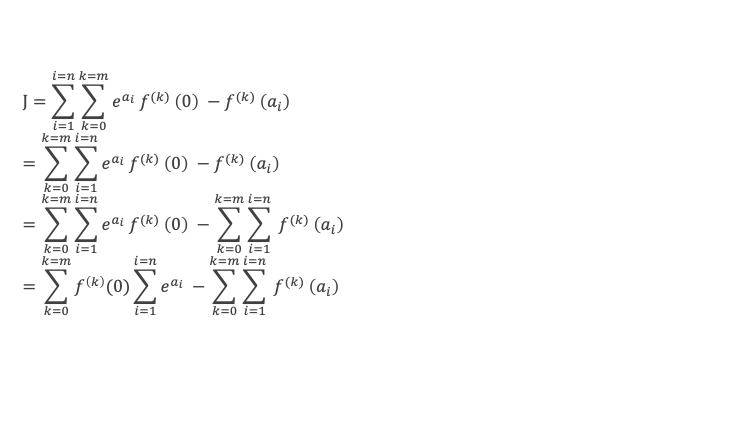
Souvenons nous de l’équation (2-1) vue à la phase 2 : 2^d – n + e^a₁ + e^a₂ + e^a₃ + e^a₄  + …. +  e^a_n-1 + e^a_n = 0. Nous avons donc

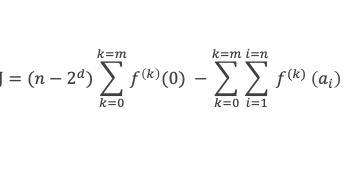
Et rappelons nous des résultats (3-1), (3-2), (3-3) qui donnent la valeur de  f^(k)(0) selon que k est inférieur ou supérieur à (p-1), ainsi que de (3-4), (3-5) qui donnent la valeur de f^(k)(a_i) en fonction de k. Il vient alors :

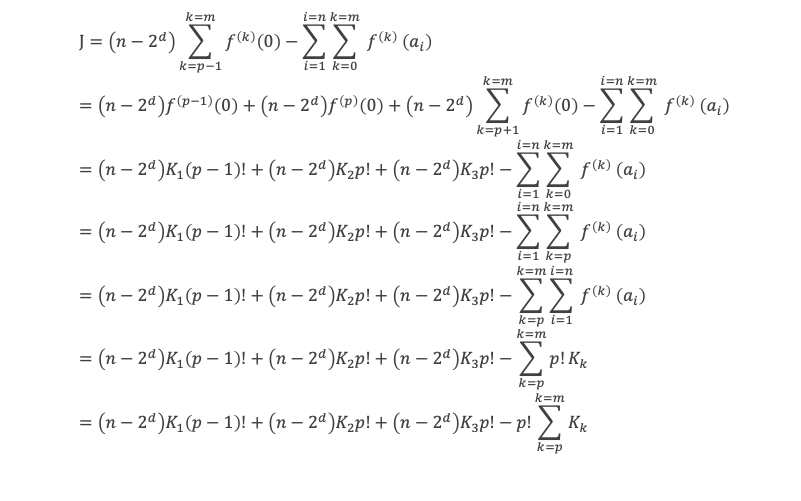
Cette dernière égalité peur être mise sous la forme : J = N₁(p -1)! + N₂p! , avec N₁ et N₂ nombres entiers relatifs, c’est à dire :

J = (p -1)! (N₁+ N₂p)

Les calculs menés en annexe montrent que f^(p-1)(0) = (-s_d )^np  (p-1)! ( a₁a₂ … a_n )^p qui est non nul, et comme (n – 2^d) est aussi non nul, l’entier relatif N₁ qui est le produit de ces 2 termes sera non nul.

Comme p peut être choisi arbitrairement, on prendra p premier > | s_dⁿa₁a₂ … a_n |, | x | signifiant valeur absolue de x. Comme p est un nombre premier l’application du petit théorème de Fermat nous dit que le reste de la division de (| s_dⁿa₁a₂ … a_n |)^p par p = | s_dⁿa₁a₂ … a_n | qui est un entier non nul, strictement inférieur à p. Ce choix de p permet donc de garantir que (s_dⁿa₁a₂ … a_n)^p n’est pas divisible par p. Si de plus on choisit aussi  p > (2^d – n) alors p ne divisera pas non plus (2^d – n) et donc p ne pourra pas diviser N₁. Avec ce choix de p on aura toujours N₁ + p N₂ ≠ 0 puisque sinon cela impliquerait que p divise N₁. Donc N₁ + pN₂ sera un entier non nul et donc | N₁ + pN₂ | ≥ 1.

Avec ce choix de p on aura aussi toujours: | J | = | (p-1)! ( N₁ + pN₂) | ≥ (p-1)! | N₁ + pN₂ | ≥ (p-1)! (3-6)

Conclusion : pour tout p premier > (2^d – n) | s_dⁿa₁a₂ … a_n | on aura | J | ≥ (p-1)! . Cela veut dire qu’à partir d’un certain rang, pour tout nombre premier p on aura | J | ≥ (p-1)!, avec J construit conformément à l’équation (3-0) à partir du polynôme f(x) de degré p. Mais par ailleurs, avec cette même valeur de p on pourra écrire :

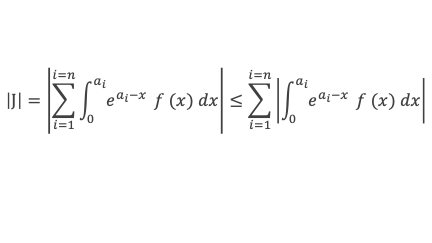
Et en repartant de la définition de f(x), à savoir f(x) = s_d^np x^p-1 (x – a₁)^p (x – a₂)^p … (x – a_n)^p, nous aurons pour tout x de l’intervalle [0 – a_i] :

Si a_i ≥ 0 : |x – a_i| = (a_i – x) ≤ a_i = |a_i|

Si a_i < 0 : |x – a_i| = (-a_i – (-x)) ≤ –a_i = |a_i|

Dans les 2 cas |x – a_i| ≤ |a_i|, ce qui permet d’écrire pour tout x de l’intervalle [0 – a_i]  : |f(x)| ≤ |s_d^np| |a_i^p-1| |a₁^p| |a₂^p| … |a_i^p| … |a_n^p|

Par ailleurs, e^{a_i – x} ≤ e^{|a_i – x|} ≤ e^|a_i| et donc pour tout x de cet intervalle :

|e^{a_i – x} f(x)| ≤ e^|a_i| |f(x)| e^|a_i| |s_d^np| |a_i^p-1| |a₁^p| |a₂^p| … |a_i^p| … |a_n^p|

D’où :

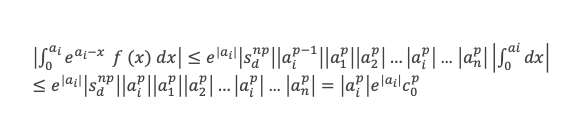
Avec c₀ = |s_dⁿ| |a₁| |a₂| … |a_i| … |a_n| qui est une constante qui ne dépend pas de p. De ce résultat on tire :

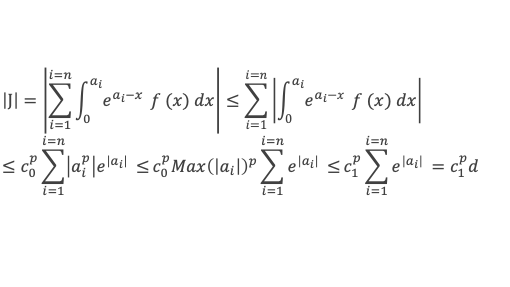
et en prenant h entier > c₁ d, on pourra écrire | J | ≤ c₁^p d ≤ c₁^pd d^p-1 ≤ h^p (3-7) avec h entier qui ne dépend pas de p.

Or, comme on l’a vu au §3 de la boîte à outils, la fonction (p-1)! croît plus vite que x^p quelque soit x, et à partir d’un certain rang p₀, tous les p vérifient (p-1)! > x^p (3-8)

Cela signifie qu’en prenant p suffisamment grand on aura :

| J | ≤ h^p. (3-7)

(p-1)! > h^p. (3-8)

| J |≥ (p-1)! (3-6)

Soit | J | < | J |

L’existence de f(x) aboutit à une contradiction. f(x) ne peut pas exister, et donc le polynôme P(X) dont π est racine qui sert à le construire n’existe pas non plus. π ne peut pas être la racine d’un polynôme à coefficients entiers, on dit π est un nombre transcendant. Comme il n’est pas racine d’un tel polynôme il ne peut pas être constructible.

Sachant que π n’est pas constructible, il reste à démontrer que √π ne l’est pas non plus Démonstration : Faisons l’hypothèse que √π soit constructible, alors le produit : √π √π = π le serait (cf  Boîte à outils §2 qui montre comment construire le produit de 2 nombres constructibles). La contradiction prouve que √π n’est pas constructible. CQFD.

√π est d’ailleurs aussi transcendant, il ne peut pas être la racine d’un polynôme à coefficient entier. Cela se démontre aisément par l’absurde : si √π est la racine d’un tel polynôme alors à partir du polynôme R(X) dont √π est la racine on peut facilement construire un polynôme dont π sera la racine, en séparant dans R(X) les monômes d’exposants paires et celui à valeur constante (qui formeront R₁(X)) et les monômes d’exposants impaires (qui formeront XR₂(X) avec R₂(X) ne contenant que des exposants paires).

R(√π) = 0 = R₁(√π) + √πR₂(√π) = S₁(π) + √πS₂(π), et donc π racine du polynôme S₁²(X) – XS₂²(X)

Annexe

Démonstration des relations (3-1) à (3-5)

A-1) Calcul des dérivées d’ordre j,  f^(j)(x) :

On note Z le produit (x – a₁)^p(x – a₂)^p … (x – a_n)^p

f ⁽¹⁾(x) = s_d^np [(p – 1)x^p-2 Z + x^p-1 Z⁽¹⁾]

f ⁽²⁾(x) = s_d^np [(p – 1)(p – 2)x^p-3 Z + 2(p – 1)x^p-2 Z⁽¹⁾  + x^p-1 Z⁽²⁾ ]

f ⁽³⁾(x) = s_d^np [(p-1)(p-2)(p-3)x^p-4 Z + 2(p – 1)(p – 2)x^p-3 Z⁽¹⁾  + (p – 1)x^p-2 Z⁽²⁾  + (p – 1)(p  -2)x^p-3 Z⁽¹⁾ + 2(p-1)x^p-2 Z⁽²⁾  + x^p-1 Z⁽³⁾] = s_d^np [(p – 1)(p – 2)(p – 3)x^p-4 Z + 3(p – 1)(p – 2) x^p-3 Z⁽¹⁾  + 3(p – 1)x^p-2 Z⁽²⁾ + x^p-1 Z⁽³⁾] 

…

f ^(j)(x) = s_d^np [(p – 1)(p – 2)(p – 3) … (p – j) x^p–j-1 Z + C_j¹ (p – 1)(p – 2) … (p – j + 1) x^p-j Z⁽¹⁾  + C_j² (p – 1)(p – 2) … (p – j + 2) x^p-j+1 Z⁽²⁾  + … + C_j^k (p – 1)(p – 2) … (p – j + k) x^p-j+k-1 Z^(k)  + …+ C_j^j-1(p – 1) x^p-2 Z^(j-1)  + x^p-1 Z^(j) ] = s_d^np [(p -1)!/(p– j – 1)! x^p-j-1 Z + C_j¹ (p – 1)!/(p – j)! x^p-j (Z) ⁽¹⁾  + C_j² (p – 1)!/(p – j + 1)! x^p-j+1 (Z) ⁽²⁾  + C_j³ (p – 1)!/(p – j + 2)! x^p-j+2 (Z)⁽³⁾ + …+ C_j^k (p-1) !/ (p–j+k-1)! x^p-j+k-1 Z^(k)  +… + C _j^j-1(p – 1)!/(p – 2)! x^p-2 (Z) ^(j-1)  + x^p-1 (Z) ^(j) ] 

…

f ^(p)(x) = s_d^np [C_p¹ (p-1)! x⁰ Z⁽¹⁾  + C_p² (p-1)! / 1! x¹ Z⁽²⁾  + C_p³ (p-1)! / 2! x² Z⁽³⁾ + … + C_p^p-1(p-1)!/(p-2)! x^p-2 Z^(p-1)  + x^p-1 Z^(p)]  = s_d^np [p(p-1)! Z⁽¹⁾  + [C_p²]/p _* (p)! / 1! x¹ Z⁽²⁾  + [C_p³]/p _* (p)! / 2! x² Z⁽³⁾ + … + [C_p^p-1]/p _* (p)!/(p-2)! x^p-2Z^(p-1)  + x^p-1 Z^(p)] = s_d^np p! [ Z⁽¹⁾  + [C_p²]/p _* x¹ Z⁽²⁾  + [C_p³]/p _* 1/2! x² Z⁽³⁾ + … + [C_p^p-1]/p _* 1/(p-2)! x^p-2 Z^(p-1)  + 1/p! _* x^p-1 Z^(p)] 

Calcul des dérivées à l’ordre j > p :

f ^(p+r)(x) = s_d^np [somme à partir de k = r+1 jusqu’à k = r+p des C_j^k (p-1)!/ (p–j+k-1)! x^p-j+k-1 Z^(k)] avec j ≥ k, formule que l’on utilisera suivant les cas sous la forme :

f ^(p+r)(x) = s_d^np p![somme à partir de k = r+1 jusqu’à k = r+p des (C_j^k/p)/ (p–j+k-1)! x^p-j+k-1 Z^(k)]

ou sous la forme :

f ^(p+r)(x) = s_d^np [somme à partir de k = r+1 jusqu’à k = r+p des  D_jk x^p-j+k-1 Z^(k)] avec j ≥ k et D_jk entier.

en effet,  C^k_j (p-1) !/(p–j+k-1)! = j!/[k!(j–k)!]_*(p-1)!/(p–j+k-1)! = j!/[k!(j–k)!] C_p-1^j–k(j–k)!= j!/k! C_p-1^j–k = entier D_jk, car C_p-1^j–k = (p-1)!/[(p–j+k-1)!(j–k)!]

A-2) Calcul des dérivées d’ordre j : f ^(j)(0) pour j ≤ p

• En appliquant les formules du § précédent pour j < p – 1, on trouve f^(j)(0) = 0 
• En appliquant la formule pour j = p-1, on trouve :

f ^(p-1)(x) = s_d^np [(p-1)! x⁰ Z + C¹_p-1 (p-1)! x¹ Z⁽¹⁾  + C²_p-1 (p-1)!/(2)! x² Z⁽²⁾  + C_p-1³ (p-1)!/(3)! x³ Z⁽³⁾ …+ C_p-1^p-2(p-1)!/(p-2)! x^p-2 Z^(p-2)  + x^p-1 Z^(p-1)]

D’où, pour x = 0, 

f ^(p-1) (0) = s_d^np (p-1)! x⁰ Z(0) = s_d^np (p-1)! (-a₁)^p (-a₂)^p … (-a_n)^p = (-s_d)^np (p-1)! (a₁a₂ … a_n)^p

• En l’appliquant pour j = p : 

f ^(p)(x) = s_d^np [C¹_p (p-1)! x⁰ Z⁽¹⁾  + C²_p (p-1)! / 1! x¹ Z⁽²⁾  + C³_p (p-1)! / 2! x² Z⁽³⁾ + … + C _p^p-1(p-1)!/(p-2)! x^p-2 Z^(p-1)  + x^p-1 Z^(p) ]  = s_d^np [ p(p-1)! Z⁽¹⁾  + [C²_p]/p _* (p)! / 1! x¹ Z⁽²⁾  + [C³_p]/p _* (p)! / 2! x² Z⁽³⁾ + … + [C _p^p-1]/p x (p)!/(p-2)! x^p-2Z^(p-1)  + x^p-1 Z^(p) ] = s_d^np p! [Z⁽¹⁾  + [C²_p ]/p _* x¹ Z⁽²⁾  + [C³_p]/p _* 1/2! x² Z⁽³⁾ + … + [C _p^p-1]/p _* 1/(p-2)! x^p-2 Z^(p-1)  + 1/p! _* x^p-1 Z^(p)] 

On trouve f ^(p)(0)  = s_d^np p! Z⁽¹⁾(0)

A-3) Calcul des dérivées d’ordre j :  f ^(j)( a_i) pour j ≤ p

On a Z(x) = S(x)^p avec S(x) = (x – a₁)(x – a₂) … (x – a_n) 

Les dérivées successives de Z(x) seront :

Z⁽¹⁾ = p S⁽¹⁾S^p-1

Z⁽²⁾ = p S⁽²⁾S^p-1 + p(p-1) (S⁽¹⁾)² S^p-2

Z⁽³⁾ = p S⁽³⁾S^p-1 +  p(p-1) S⁽²⁾ S⁽¹⁾S^p-2 + 2p(p-1) S⁽²⁾ S⁽¹⁾ S^p-2 + p(p-1)(p-2) (S⁽¹⁾)³ S^p-3

      = p S⁽³⁾S^p-1 +  3p(p-1) S⁽²⁾ S⁽¹⁾S^p-2 + p(p-1)(p-2) (S⁽¹⁾)³ S^p-3

Z⁽⁴⁾ = p S⁽⁴⁾S^p-1 +  4p(p-1) S⁽³⁾ S⁽¹⁾S^p-2 + 3p(p-1) S⁽²⁾ S⁽²⁾S^p-2  +  6p(p-1)(p-2) S⁽²⁾ (S⁽¹⁾)²S^p-3

+ p(p-1)(p-2)(p-3)(S⁽¹⁾)⁴ S^p-4

      = p S⁽⁴⁾S^p-1 +  p(p-1) [4S⁽³⁾ S⁽¹⁾ + 3S⁽²⁾ S⁽²⁾]S^p-2  +   6p(p-1)(p-2) S⁽²⁾ (S⁽¹⁾)²S^p-3

+ p(p-1)(p-2)(p-3)(S⁽¹⁾)⁴ S^p-4

…

Z(j) = p S(j)Sp-1 +… + somme de termes de la forme Kk[(S(i1).)k1 *…* (S(iu).)ku]Sp–k +… + p(p-1)(p-2)(p-3)…(p–j+1)(S(1))j Sp–j

…

Z(p) = p S(p)Sp-1 + somme de termes de la forme Kk[(S(i1).)k1 *…* (S(iu).)ku]Sp–k + p(p-1)(p-2)(p-3)…(1)(S(1))p S0

Tant que l’exposant k de S dans ces formules est  > 0, on a S^k(a_i) = 0 pour chaque a_i. On en déduit que toutes les dérivées k-ième de Z pour k = 1 à p-1 vérifient Z^(k)(a_i) = 0 quel que soit a_i, et donc que f ^(k)(a_i) = 0 pour tout a_i avec k de 1 à p-1.

A ce stade nous avons donc la collection de résultats suivants : 

• Pour j < p-1 : f^(j)(0) = 0.  (3-1)
• Pour j = p-1 : f^(p-1)(0) = (-s_d)^np (p-1)! (a₁a₂ … a_n)^p
• f ^(p)(0)  = s_d^np p! Z⁽¹⁾(0)
• Pour j < p : f ^(j)(a_i) = 0 pour tout a_i   (3-4)

Il nous reste à démontrer les 4 points suivants:

1. Que (-s_d)^np(a₁a₂ … a_n)^p est entier, pour finaliser (3-2)
2. Que s_d^np Z⁽¹⁾(0) est entier, pour le cas k = p de (3-3)
3. Que f ^(k)(0)  = p! _* (nombre entier ) pour k > p pour finaliser (3-3)
4. Que Σ₁ⁿ f ^(j)(a_i) est multiple entier de p! lorsque j ≥ p pour finaliser (3-5)

A-4) Démonstration des 2 premiers points : (-s_d)^np(a₁a₂ … a_n)^p et s_d^np Z⁽¹⁾(0) sont entiers. 

Pour cela rappelons-nous d’abord de la définition des a_i : 

 a_i  = e₁.q₁ + e₂.q₂ + e₃.q₃ + … + e_k. q_k + … + e_d-1.q_d-1 + e_d.q_d , les e_k valant 0 ou 1 avec q₁, q₂, q₃, … q_d les racines du polynôme à coefficients entiers P(X)= s₀ + s₁x + s₂x² + … s_kx^k + … + s_d x^d . Les d premiers a_i sont les q₁, q₂, … , q_d, les suivants sont les a_i de la forme (q_i + q_j) avec i et j différents, puis les suivants sont les a_i de la forme (q_i + q_j + q_k) avec i, j, k différents, puis etc… jusqu’à a_n = q₁ + q₂ + q₃ + … + q_k + … + q_d-1 + q_d.

Comme les q_i sont les racine de P(x),  P(x) s’écrit aussi, de façon équivalente :

P(x) = s_d (x – q₁)(x – q₂) … (x – q_k) … (x – q_d-1)(x – q_d) ce qui après développement donne :

P(x) = s_d x^d + s_d (q₁ + q₂ + … + q_k … + q_d-1 + q_d) x^d-1 + s_d (Σq_iq_j) x^d-2 + s_d (Σq_iq_jq_k) x^d-3 + … + s_d (somme de tous les produits de k termes q_i différents) x^d–k + … + s_d (somme de toutes les produits de d-2 termes q_i différents) x² + s_d (somme de tous les produits de d-1 termes  q_i différents ) x +(-1)^d s_d q₁ q₂ … q_k … q_d-1 q_d

Par identification avec P(x) on tire :

s_d (q₁ + q₂ + … + q_k … + q_d-1 + q_d) = s_d-1

s_d (Σq_iq_j) = s_d-2

s_d (Σq_iq_jq_k)= s_d-3

…

s_d (somme de tous les produits de k termes q_i différents) = s_d–k

…

(-1)^ds_d q₁ q₂ … q_k … q_d-1 q_d = s₀

Avec chacun des termes s_i qui est un entier.

On en déduit que tous les polynômes symétriques élémentaires construits à partir des d racines q_i sont de la forme : s_i / s_d avec s_i et s_d entiers. C’est-à-dire, en reprenant la notation vue au §4 de la boîte à outils :

PS₁ : s_d-1/s_d, PS₂ = s_d-2/s_d, … , PS_k = s_d–k/s_d, … ,PS_d = (-1)^ds₀/s_d

Considérons maintenant le produit de tous les a_i :

a₁a₂ … a_n = Π a_i = Π q_i * Π (q_i+q_j) _* Π (q_i+q_j+q_k) _* … _* Π (somme de k des d racines) _* (q₁ + q₂ + … + q_k … + q_d-1 + q_d). Ce produit est une fonction symétrique sur les d indices des racines, il s’exprime donc comme une combinaison des polynômes symétriques élémentaires PS₁, PS₂, PS_k, … PS_d. On constate également que Π a_i est le produit de n termes de degré 1 car les a_i sont de degré 1 lorsqu’ils sont exprimés en q_i. Sachant que chaque polynôme symétrique élémentaire PS_i est de degré i, cela implique que Π a_i s’écrit sous la forme :

Π ai = Somme de termes (PS1)a1*(PS2)a2*…*(PSk)ak* … (PSd-1)ad-1*(PSd)ad dont chacun des vérifie la condition :

a₁ + 2a₂ + 3a₃ + … + ka_k + … + (d-1)a_d-1 + da_d = n, où les a_i sont les exposants des PS_i

On aura donc finalement :

Π ai = Somme de termes (sd-1/sd)a1*( sd-2/sd)a2*…*( sd–k/sd)ak* … (s1/sd)ad-1*((-1)ds0/sd)ad = M1/( sd)a1 + a2 + a3 + … + kak + … + ad-1 + ad = (M1)a2 + 2a3 + … + (k-1)ak + … + (d-2)ad-1 + (d-1)ad /( sd)a1 + 2a2 + 3a3 + … + kak + … + (d-1)ad-1 + dad = Kd/sdn avec M1 et Kd nombres entiers relatifs.

Conclusion : a₁a₂ … a_n = K_d / s_dⁿ avec K_d entier relatif.

Cela permet de conclure aussi : (-s_d)^np(a₁a₂ … a_n)^p = (-s_d)^np(K₀ / s_dⁿ)^p est un entier, donc f^(p-1)(0) = (-s_d)^np (p-1)! (a₁a₂… a_n)^p est un entier multiple de (p-1)!

Examinons maintenant Z⁽¹⁾(x) :

Z (x) = (x – a₁)^p (x – a₂)^p … (x – a_n)^p

Commençons par étudier S(x) = (x – a₁)(x – a₂) … (x – a_n-1)(x – a_n) 

S(x) = xⁿ + (Σa_i) x^n-1 + (Σa_ia_j) x^n-2 + ((Σa_ia_ja_l) x^n-3 + …+    (Σ produit de k termes a_i) x^n-k + (Σ produit de n-1 termes a_i) x + (a₁a₂ … a_n-1a_n)

On a vu précédemment que a₁a₂ … a_n-1a_n = nombre entier / ( s_d )ⁿ , de même a₁ + a₂ + a₃ + a₄ + … +  a_n est la somme de : Σ q_i + Σ (q_i+q_j) + Σ (q_i+q_j+q_j)  + … + (Σ k des d q_i)  + … + (q₁+q₂ +…+q_k …+q_d-1+q_d). C’est un polynôme symétrique sur les q_i, il s’exprime donc en fonction des polynômes symétriques élémentaires PS_i et comme il est de degré 1 en q, il s’écrit forcément sous la forme d’un entier multiplié par PS₁ puisque chaque q_i est présent un nombre entier de fois dans cette somme. Donc :

a₁ + a₂ + a₃ + a₄ + … +  a_n = entier_*PS₁ = K₁/s_d avec K₁ entier.

De même Σa_ia_j est la somme de toutes les sommes possibles de 1 ou 2 ou 3 ou k ou…d q_i (qui sont les a_i) par des sommes de q_i du même type mais qui donnent un résultat différent (a_i doit être différent de a_j), le produit résultant s’exprime forcément comme une somme de termes en Σq_iq_j , chacun de ses monômes est de degré 2 en q, et c’est un polynôme symétrique sur les q_i. Le produit résultant est donc construit comme une somme de PS₁² et de PS₂. Il s’écrit forcément sous la forme : entier _* (s_d-1/s_d)² + entier _* s_d-2 / s_d = K₂/( s_d)² avec K₂ entier.

De même Σa_ia_ja_l est la somme des produits de :

– toutes les sommes possibles de q_i (qui donnent les a_i)

– par des sommes de q_i du même type mais qui donnent un résultat différent (a_j doit être différent de a_i)

– par des sommes de q_i du même type mais qui donnent encore un résultat différent des sommes précédentes (a_k différent de a_j ou a_i)

Le résultat s’exprime forcément comme une somme symétrique sur les d indices des q_i, et avec des termes de degré 3 en q, donc forcément à partir de PS₁³, PS₁*PS₂, et PS₃. 

Le produit résultant s’écrit forcément sous la forme : entier _* (s_d-1/s_d)³ + entier _* s_d-2 s_d-1 /(s_d)² + entier + s_d-3/s_d = K₃/(s_d)³ avec K₃ entier.

Le même raisonnement tient pour tous les termes de la forme (Σproduit de k termes a_i) qui constituent les coefficients du polynôme S(x) = (x – a₁)(x – a₂) … (x – a_n-1)(x – a_n), ce qui permet de conclure que les coefficients de ce polynôme sont tous de la forme : K_i/( s_d)ⁱ avec i de 0 à n, et avec K_i entier (K₀ = 1).

Ce résultat permet d’affirmer que les coefficients du polynôme Z = S(x)^p sont de la forme : entier /( s_d)^j avec j de 0 à np. Donc tous les coefficients de s_d^np Z(x) sont entiers et ce sera encore le cas pour les dérivées de s_d^np Z(x) puisque la dérivée des monômes d’un polynôme ne fait que multiplier par des entiers les coefficients du monôme de départ, donc s_d^np Z⁽¹⁾(x) est à coefficients entier, or s_d^np Z⁽¹⁾(0) est l’un de ces coefficients, il est donc entier.

Les 2 premiers points ont été démontrés.

A-5) A ce stade, il ne reste à démontrer que :

1. f ^(k)(0)  = p! _* (nombre entier ) pour k > p pour finaliser (3-3)
2. Σ_i=1ⁿ f^(j)(a_i) est multiple entier de p! pour finaliser (3-5)

Considérons de nouveau S(x). Il ressort du paragraphe précédent que S(x) s’écrit : 

S(x) = xⁿ + (Σa_i) x^n-1 + (Σa_ia_j) x^n-2 + ((Σa_ia_ja_l) x^n-3 + …+    (Σproduit de k termes a_i) x^n–k + (Σproduit de n-1 termes a_i) x + (a₁a₂ … a_n-1a_n) 

= xⁿ + K₁/s_d x^n-1 + K₂/(s_d)² x^n-2 + K₃/(s_d)³ x^n-3 + …+ K_k/(s_d)^k  x^n–k + … + K_n-1/(s_d)^n-1 x + K_n / s_dⁿ avec K_i entier pour i de 1 à n.

Z(x) = S(x)^p  sera la somme des termes suivant, classés par degré décroissant :

•  x^np , produit des p monômes de plus haut degré xⁿ, 
• K₁/s_d x^n(p-1)+n-1 , produit de p-1 monômes de plus haut degré (xⁿ) et du monôme de degré n-1 (K₁/s_d x^n-1), 
• [K₂/(s_d)²+ (K₁/s_d)²] x^n(p-1)+n-2 , produit de p-1 monômes de plus haut degré (xⁿ) et d’un monôme de degré n-2  (K₂/(s_d)² x^n-2) ou de p-2 monômes de degré n (xⁿ) avec 2 monômes de degré n-1 (K₁/s_d x^n-1), 
• …
• Monôme de degré k, produit de p monômes de degré respectifs δ₁, δ ₂, … δ _p tels que δ₁ + δ₂ + … + δ_j = k, chacun de ces monômes ayant pour coefficient K_n–δi/(s_d)^n–δi de sorte que le monôme de degré k aura pour coefficient D_k/(s_d)^np-Σδi = D_k/(s_d)^np-k

Le terme général du polynôme Z(x) s’écrit donc pour k de 0 à np : D_k/(s_d)^np–k x^k avec D_k entier, et la dérivée j^ième de ce terme sera de la forme: (k)(k-1)…(k–j+1)D_k /(s_d)^np–k x^k–j pour j de 1 à k, et = 0 pour j > k. 

Pour j de 1 à k cela donnera les termes :

jD_j /(s_d)^np–j + (j+1)(j+2) D_j+1 /(s_d)^np–j-1 x +…+(j+i)(j+i-1)…(i+1)D_j+i /(s_d)^np–j–i xⁱ + …

Revenons à f^(k)(x) pour calculer f^(k)(0) avec k > p.

f ^(p+r)(x) = s_d^np p! _* [somme à partir de k = r+1 jusqu’à k = r+p des C^k_p+r /p _*1/(k–r-1)! x^k–r-1 Z^(k)]. Pour x = 0, le seul terme non nul correspond à k = r+1 ce qui donne :

f ^(p+r)(0) = s_d^np p! _* [C^r+1_p+r /p Z^(r+1)(0)]. Or comme on vient de le voir :

Z^(r+1)(x) = (k)(k-1)…(k-(r+1)+1)D_k /(s_d)^np–k x^k-(r+1), là encore pour x = 0 seul le terme non nul est obtenu avec k = r+1.

Z^(r+1)(0) = (r+1)! D_k /(s_d)^np-(r+1)  

Par ailleurs C^r+1_p+r = (p+r)!/(r+1)!(p-1)! = (p+r)(p+r-1) … (p)/(p-1)! d’où :

f ^(p+r)(0) = s_d^np p! _* [C^r+1_p+r /p (r+1)! D_k /(s_d)^np-(r+1)] = s_d^np p ! (p+r)(p+r-1) …(p+1) D_k /(s_d)^np-(r+1) = s_d^(r+1) p ! (p+r)(p+r-1) …(p+1) D_k avec D_k et s_d entier.

Ce résultat finalise (3-3).

Il reste à montrer que Σ_i=1ⁿ f^(j)(a_i) est entier, multiple de p! lorsque j ≥ p pour finaliser (3-5).

f(x) = s_d^np x^p-1 Z(x) et comme Z(x) est une somme de monômes de la forme D_k/(s_d)^np–k x^k avec D_k entier, on en déduit que f(x) est une somme de monômes de la forme : s_d^k D_k x^k+p-1

La dérivée j-ième de chacun de ces monômes donnera s_d^k(k+p-1)(k+p-2) …(k+p-j) D_k x^k+p-1-j

• Pour j = p on trouvera des monômes de la forme : s_d^k(k+p-1)(k+p-2) …(k) _* D_k x^k-1 et en remarquant que (k+p-1)(k+p-2) …(k) = (k+p-1)!/(k-1) ! et que C_k+p-1^k-1 = (k+p-1)!/(k-1)!p! on obtient (k+p-1)(k+p-2) …(k) = p! _* C_k+p-1^k-1 ce qui permet d’écrire les monômes de f(x)^(p) sous la forme : s_d^k p! _* C_k+p-1^k-1 _* D_k x^k-1 = s_d^k p! _* E_{k0 *} x^k-1 avec E_k0 entier.
• Pour j > p on trouvera des monômes de la forme : s_d^k(k+p-1)(k+p-2) …(k+p–j) D_k x^k-1+p–j et en remarquant que (k+p-1)(k+p-2) …(k+p–j) = (k+p-1)!/(k+p–j-1)! et que C_k+p-1^k+p–j-1 = (k+p-1)!/(k+p–j-1)!j! on obtient (k+p-1)(k+p-2) …(k+p–j) = j! _* C_k+p-1^k+p–j-1 ce qui permet d’écrire les monômes de f(x)^(j) sous la forme : s_d^k j! _* C_k+p-1^k+p–j-1_* D_kj x^k+p-j-1. Comme j > p, le monôme peut être écrit s_d^k p! _* E_{kp–j *} x^k+p–j-1avec E_kj entier.

D’une façon générale, pour j ≥ p, f(x)^(j) = somme de monômes de la forme s_d^k p! _* E_{kp-j *} x^k+p–j-1, que l’on peut reformuler en Σ s_d^k p! _* E_{ku *} x^k–u-1 avec u= p–j indice allant de 0 à k-1.

Appliquons ce résultat à a_i :

f(a_i)^(j) = Σ_u=0^k-1 s_d^k p! _* E_{ku *} a_i^k–u-1 et donc :

Σ_i=1ⁿ f(a_i)^(j) = Σ_i=1ⁿ Σ_u=0^k–1 s_d^k p! _* E_{ku *} a_i^k–u-1 = p! Σ_u=0^k-1 s_d^k E_ku(Σ_i=1ⁿa_i^k–u-1)

La somme Σ₁ⁿa_i^k–u-1 est symétrique sur les a_i^k–u-1 et l’exposant k–u-1 vaut au plus k-1. Cette somme s’exprime par une combinaison de polynômes symétriques élémentaires en ai qui sera au plus de degré k-1 en termes qi, on en déduit Σ₁ⁿa_i^k–u-1 = entier/s_d^k.

Cela permet de conclure : Σ₁ⁿ f(a_i)^(j) = p! * entier lorsque j ≥ p. Ce résultat finalise (3-5).