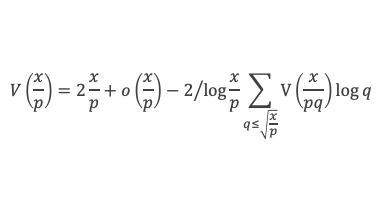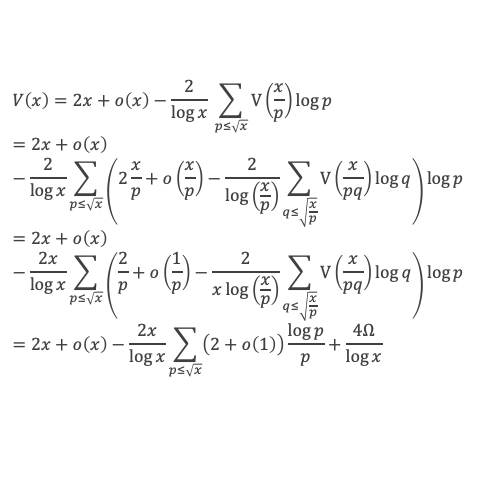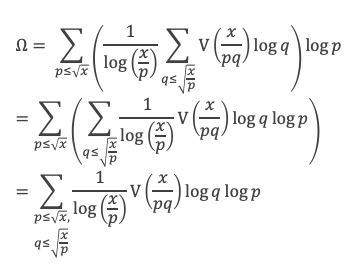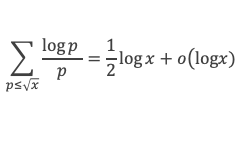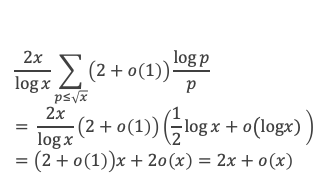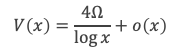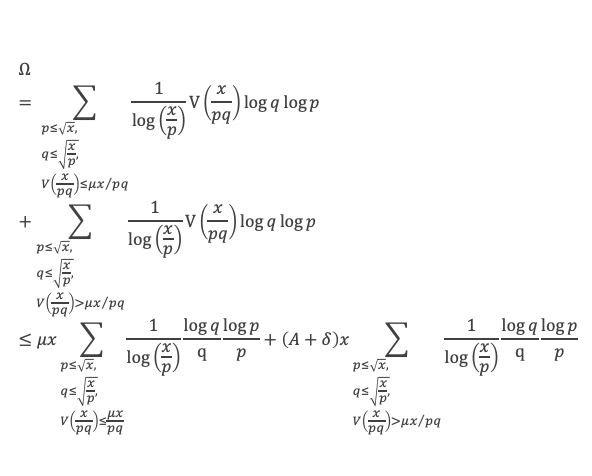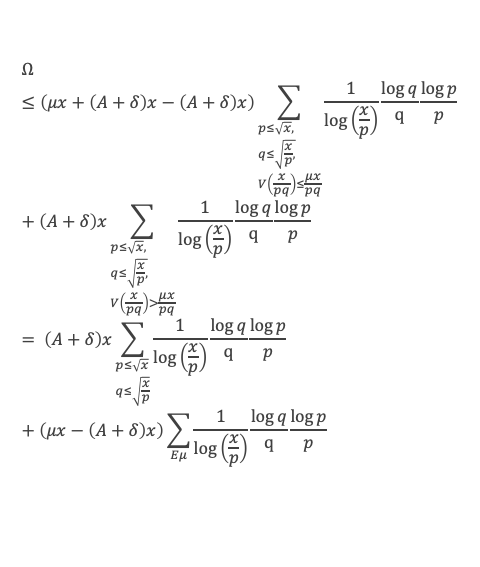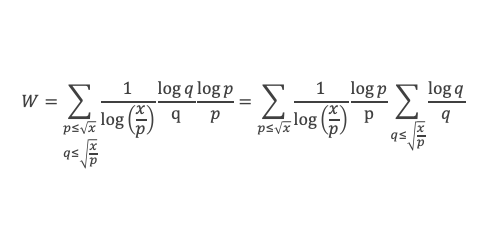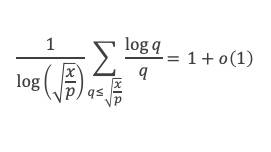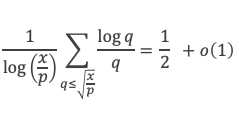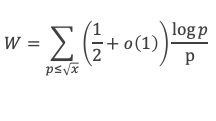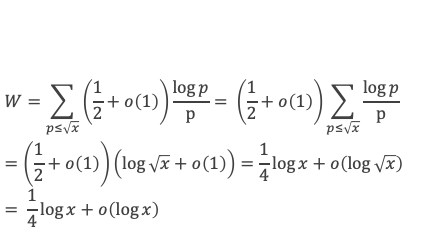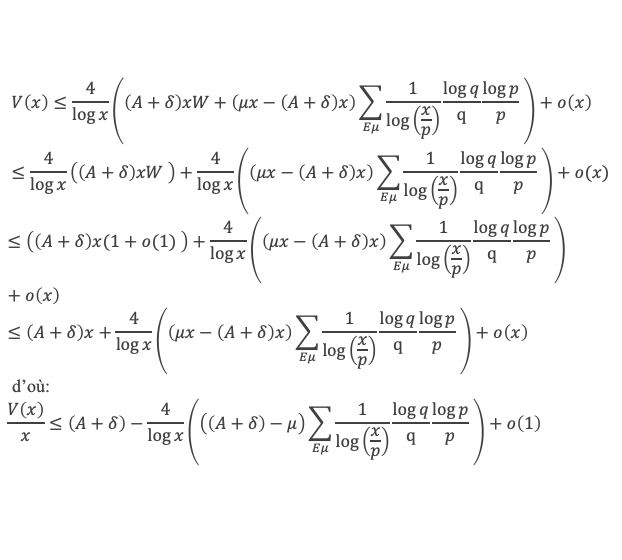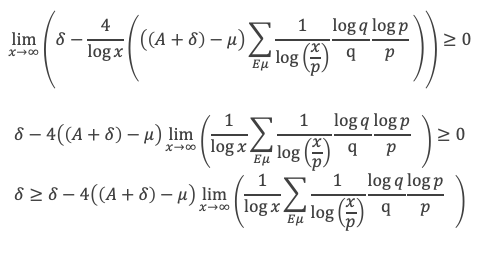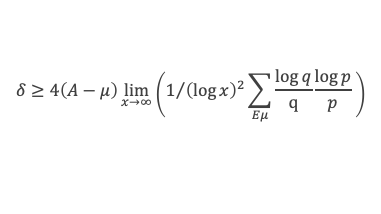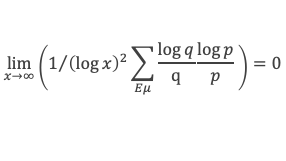
Enoncé

La fonction π qui à un réel x associe π (x) le nombre de nombres premiers inférieurs ou égaux à x, est équivalente lorsque x tend vers +∞, au quotient de x par son logarithme népérien: 

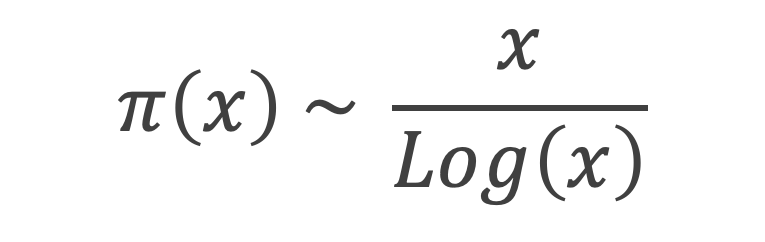
Histoire du théorème

Le théorème des nombres premiers a été conjecturé dans la marge d’une table de logarithmes par Gauss en 1792 ou 1793 alors qu’il avait seulement 15 ou 16 ans (selon ses propres affirmations), puis par Adrien-Marie Legendre qui conjectura en 1808 que π (x) est approximé par la fonction :

x / ( A log x + B ) , où A et B sont des constantes.

Le Russe Pafnouti Tchebychev a établi en 1851 que si x est assez grand, π (x) est compris entre 0,92129 x/log(x) et 1,10556 x/log(x).

Le théorème a finalement été démontré indépendamment par Jacques Hadamard et Charles Jean de La Vallée Poussin en 1896 à l’aide de méthodes d’analyse complexe, utilisant en particulier la fonction ζ de Riemann. Au cours du 20e siècle, il a aussi fini par prendre le nom de théorème des nombres premiers (TNP). 

Plusieurs démonstrations en ont été trouvées, dont les preuves ’’élémentaires’’ d’ Atle Selberg et Paul Erdős (1949). Ces preuves ont introduit diverses simplifications qui évitent l’analyse complexe, mais elles restent très lourdes. En 1980, le mathématicien américain Donald J. Newman apporte une nouvelle preuve qui est à ce jour sans doute la plus courte des preuves connues.  Courte mais pas vraiment élémentaire dans le sens où elle utilise le théorème intégral de Cauchy issu d’une analyse complexe. 

La version présentée dans cette article est celle d’ Atle Selberg et Paul Erdős présentée le 30 octobre 1948 à Amsterdam, mise en forme par J.G. Van der Corput sur la base des notes qu’il a prises lors de cette conférence. Elle est élémentaire, donc ne nécessite que des connaissances de base en mathématiques, la contrepartie est qu’elle est très longue et nécessite du temps pour la digérer.

Ref : Démonstration élémentaire du théorème sur la distribution des nombres premiers, Mathematisch centrum, ‘49’, Amsterdam.

Les grandes lignes de la démonstration

On note p, nombre premier

On note π (x)  la fonction donnant le nombre de nombre premiers inférieurs à x.

On note V(x) la fonction définie par : V(x) = ∑_p<x log p, la somme des logarithmes des nombres premiers inférieurs à x.

La fonction V(x) est une fonction croissante, c’est-à-dire que si x₂ > x₁ alors V(x₂) > V(x₁).

On sera amené à utiliser les coefficients du binôme de Pascal, que l’on notera dans le fil du texte (k¦n), ou bien dans les formules sous leur expression habituelle :

1^ère Etape : Dans un premier temps on montre que:

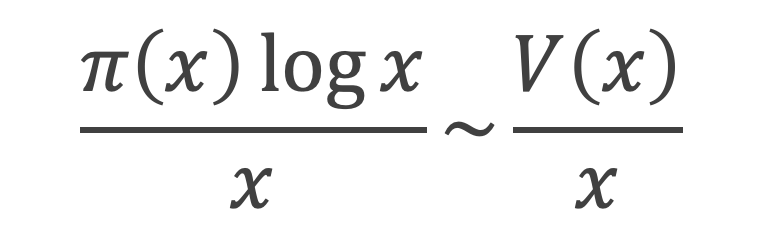
L’enjeu de la suite de la démonstration devient alors de montrer que :

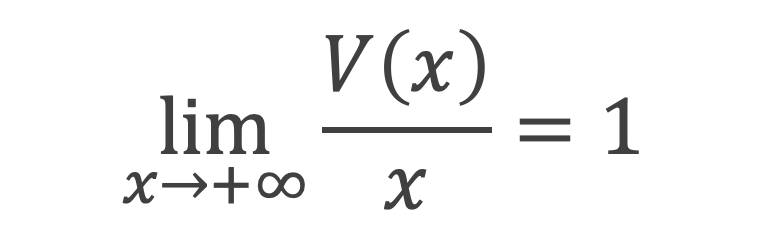
2^ième Etape : Mise en place d’un étau sur V(x)/x :

Pour cela on montre que que V(x)/x est encadré par 2 bornes, 2 constantes réelles positives a et A telles que  :

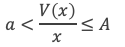
3^ième étape : L’étau se resserre :

En s’appuyant sur la formule de A. Selberg, on montre que : a + A = 2. 

Le principal effort durant cette étape consiste à démontrer la formule de Selberg, ce qui est assez laborieux. La démonstration nécessite 12 lemmes préparatoires, dont 8 sont démontrés dans la partie boîte à outils. Une fois la formule de Selberg acquise, la démonstration de l’égalité a + A = 2 est rapide.

4^ième étape : L’étau est complétement refermé

La preuve se termine par la démonstration que a = A, ce qui compte tenu de (a + A) = 2, implique que a = A = 1

Boîte à outils

1- Dans toute la suite de l’article, les lettres p et q désigneront toujours un entier premier.

2- Toute puissance réelle de x (c’est-à-dire x^α avec α positif) est inférieure à la fonction exponentielle exp(x) à partir d’un certain rang ; c’est-à-dire : lim (x^α/exp(x)) = 0 quand x tend vers l’infini. Cela se déduit immédiatement du fait que la fonction log(x) / x tend vers 0 lorsque x tend vers l’infini. En effet, on aura pour tout réel α positif : log(x^α/exp(x)) = α log(x) – x = x (α log(x)/ x – 1) qui tend vers – x, c’est-à-dire –∞  lorsque x tend vers +∞, et si log(x^α/exp(x)) tend vers –∞ cela signifie que exp( log(x^α/exp(x)) ) = x^α/exp(x) tend vers exp(–∞) c’est-à-dire 0.

3- On note o(f(x)) une fonction telle qui devient négligeable par rapport à f(x)  lorsque x tend vers l’infini, c’est-à-dire telle que le rapport o(f(x)) / f(x) tende vers 0 quand x tend vers l’infini.

4- Fonction de Möbius : On note μ(m) la fonction de Möbius, définie sur N, par:

• μ(1) =1, 
• μ(m) = 0 si m est divisible par un carré > 1, et dans les autres cas μ(m) = +1 ou -1 selon que le nombre de facteurs premiers de n est pair ou impair.

La fonction de Möbius est une fonction multiplicative, c’est-à-dire que l’on a μ(ab) = μ(a) μ(b), si a et b sont premiers entre eux.

5- La démonstration de la formule de Selberg s’appuie sur 12 lemmes. Les lemmes 1, 2, 7, 8, 9, 10, 11 et 12 forment une suite cohérente et nous avons fait le choix de les traiter dans ce paragraphe de boîte à outils de façon à ce que l’exposé de la démonstration de la formule de Selberg puis du théorème s’en trouve allégée. Voici les 8 lemmes en question et leur démonstration.

6- Lemme 1 : Notons C_n(m) la fonction définie par:

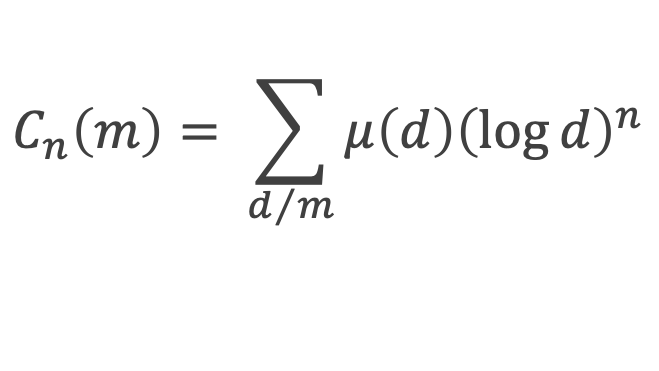
Où la somme est étendue à tous les diviseurs d de m, 1 et m compris.

Le lemme 1 affirme que si m contient plus de n facteurs premiers différents alors pour tout k entier positif < n la fonction C_k(m) vérifie, pour m > 1:

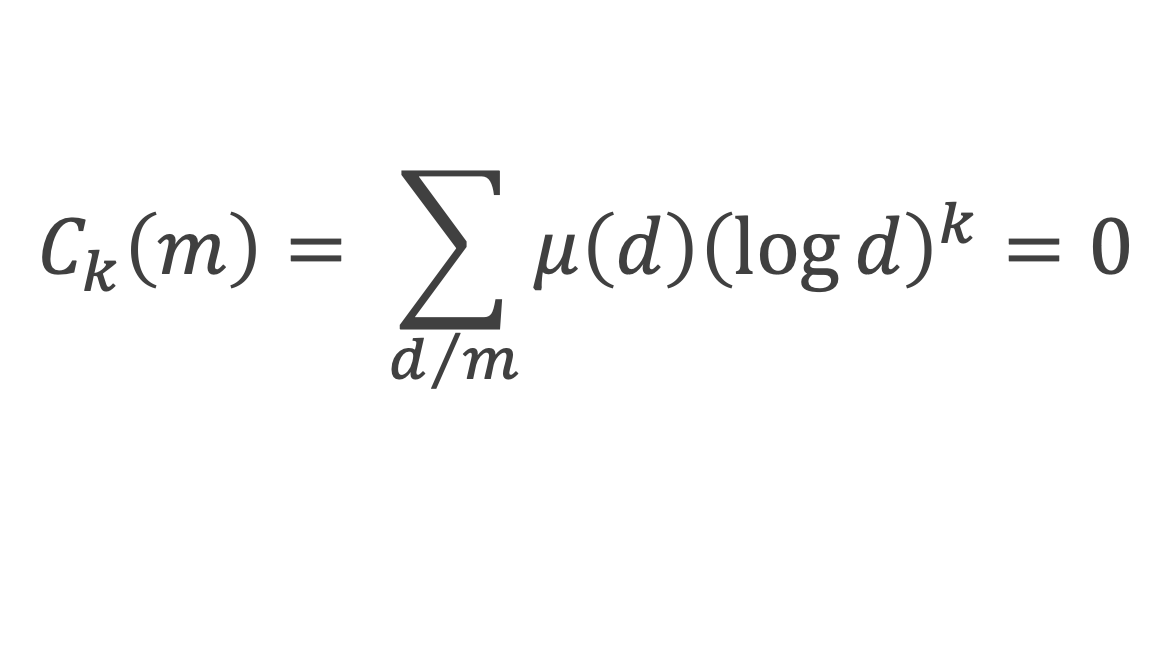
Démonstration du lemme 1 : la démonstration va être faite par récurrence, en commençant par le cas n= 0, puis en démontrant que lorsque la propriété est vraie pour n-1, elle l’est aussi pour n.

Cas n = 0 : il faut démontrer que ∑_d/m μ(d) = 0 pour tout m > 1

Soit m entier qui se décompose en r facteurs premiers (r > 0), 

m = p₁^α1 p₂^α2 p₃^α3… p_r-1^αr-1 p_r^αr

Tous les diviseurs de d dont la décomposition comprend un exposant > 2 donneront un μ(d) = 0, donc les seuls diviseurs d de m à considérer pour le calcul de ∑_d/m μ(d) sont ceux de la forme :

d = p₁^β1 p₂^β2 p₃^β3… p_r-1^βr-1 p_r^βr, avec β_i = 0 ou 1

• Il y a un seul diviseur avec tous les β_i = 0, d = 1 et μ(d) = 1
• Il y en a (1¦r) avec un seul b_i = 1 et les autres = 0. Pour chacun de ces diviseurs μ(d) = -1, leur contribution à la somme est -(1¦r)
• Il y en a (2¦r) avec exactement 2 β_i = 1 et les autres = 0. Pour chacun de ces diviseurs μ(d)  = 1, leur contribution à la somme est (2¦r)
• …
• Il y en a (r-1¦r) avec exactement (r-1) β_i = 1 et 1 β_i = 0. Pour chacun de ces diviseurs μ(d) = (-1)^r-1, leur contribution à la somme est (-1)^r-1(r-1¦r)
• Il y en a (r¦r) avec exactement tous les β_i = 1. Pour ce diviseur μ(d)  = (-1)^r, sa contribution à la somme est (-1)^r(r¦r)

On aura donc au total

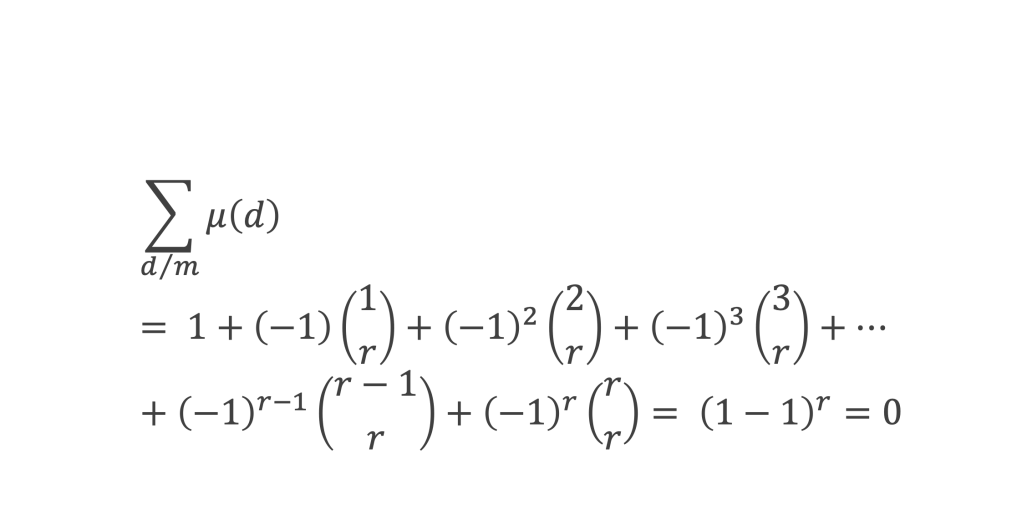
Le cas n = 0 est donc démontré.

Supposons maintenant que le cas n-1 soit vrai, démontrons qu’alors ∑_d/m μ(d)(log d)ⁿ = 0 pour tout m comprenant au moins n facteurs premiers.

La propriété est vraie au rang n-1 signifie que pour tout m contenant au moins n-1 facteurs premiers ∑_d/m μ(d)(log d)^k = 0 pour k de 0 à n-1.

Considérons m entier qui se décomposerait en au moins n facteurs premiers. m s’écrit : m = p^αb, avec p premier, α > 1, b non divisible par p, et b comprenant au moins n-1 facteurs premiers.

Tout diviseur d de p^αb s’écrit d₁d₂ avec d₁ diviseur de p^α et d₂ diviseur de b.

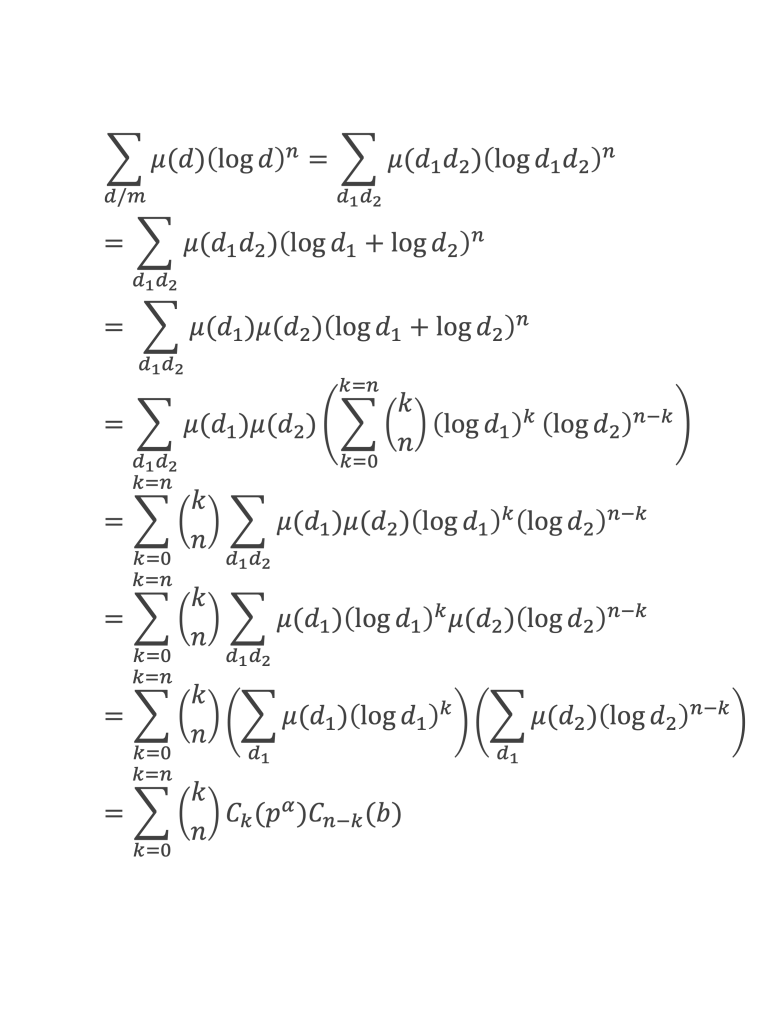
Les C_n-k(b) = 0 de k = 1 à n, il ne reste donc plus dans la somme que le terme C₀ (p^α)C_n(b) et l’on sait que C₀ (p^α) = 0.

Le cas n est donc aussi démontré lorsque n-1 est vrai. Le lemme 1 est démontré.

7- Lemme 2 : Soit x  > 0, posons Λ_x(d) = μ(d) (log x/d)² et f_x(m) = ∑_d/m Λ(d), alors :

f_x (1) = log²x                                                                                        (1)

f_x (p^α) = -log²p + 2 (log x) (log p) avec p premier et a > 1                 (2)

f_x (p^αq^β ) = 2 (log p) (log q) avec p et q premiers et α et β > 1         (3)

f_x (m) = 0 si m contient plus de 2 facteurs premiers différents.        (4)

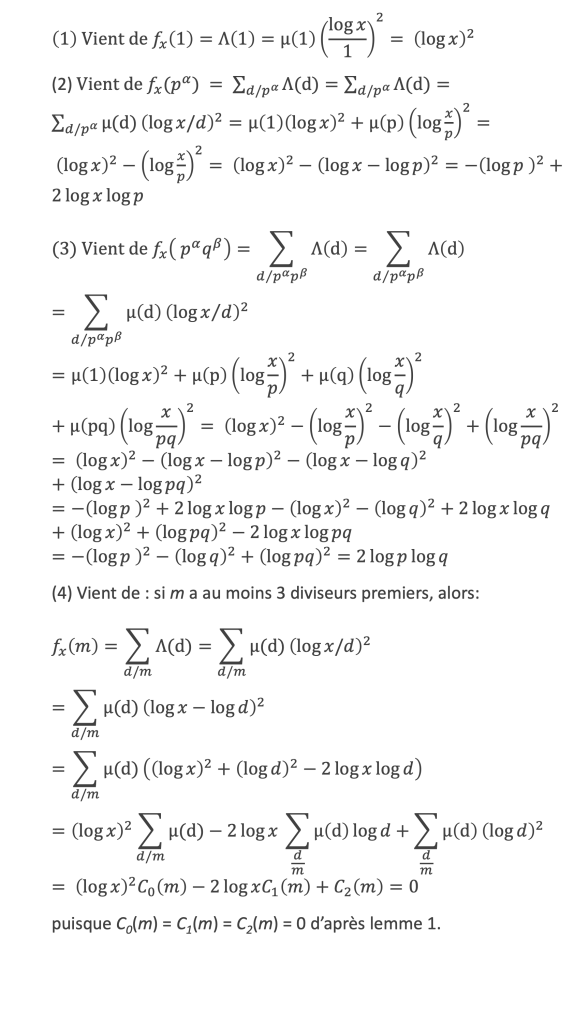
8- Lemme 7 : On a pour chaque entier n : 

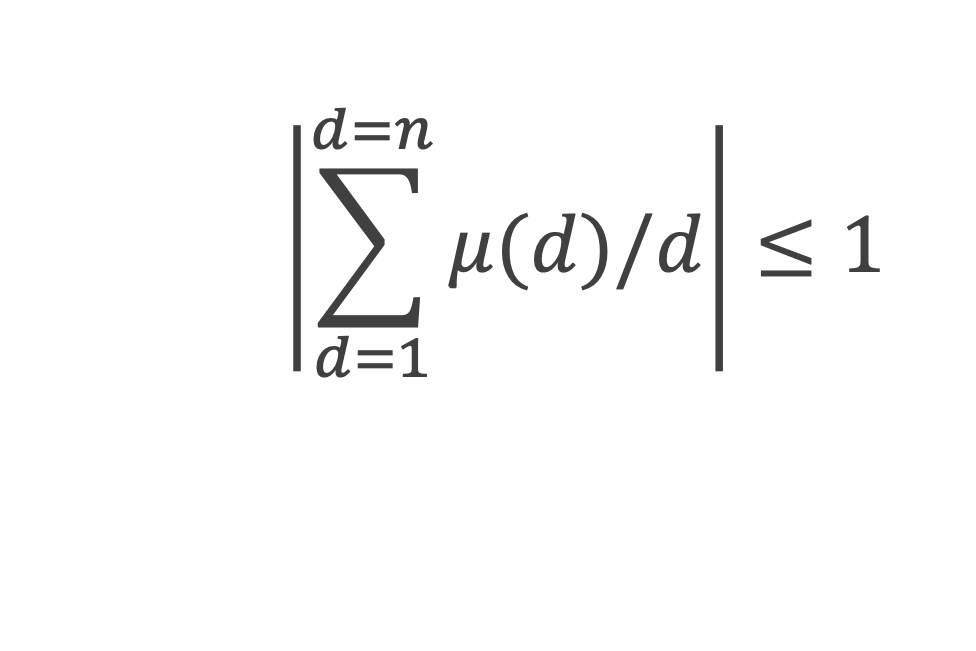
En effet : ∑_d/m μ(d) = 1 pour m = 1,  et = 0 pour m > 1 Donc : 

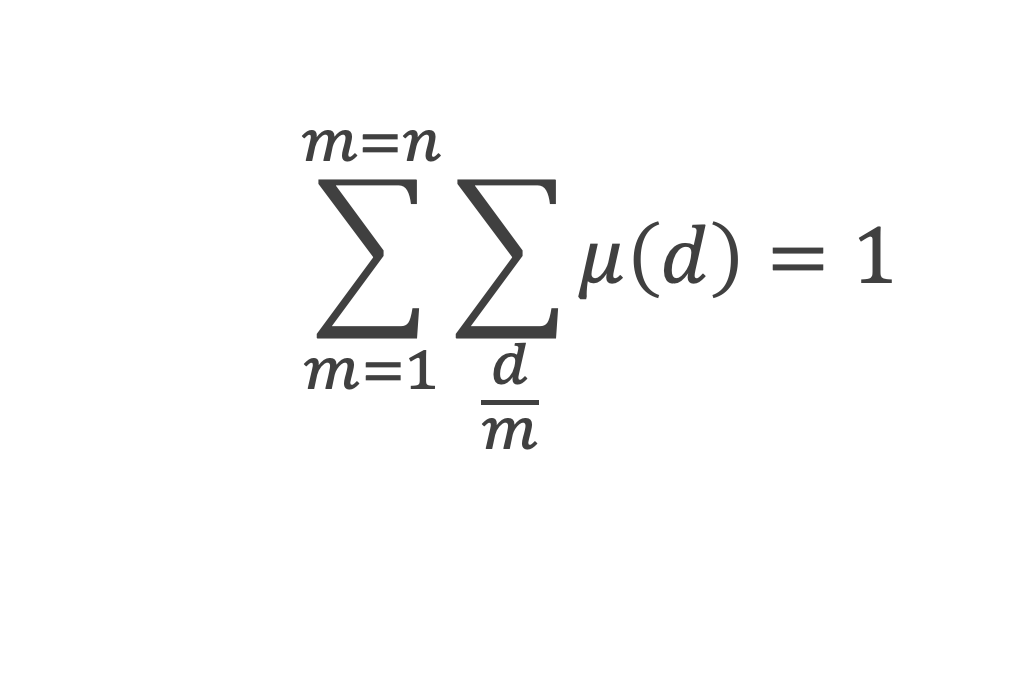
Chaque diviseur d de cette double somme va donner le terme μ(d) pour chaque multiple < n de d. On obtient :

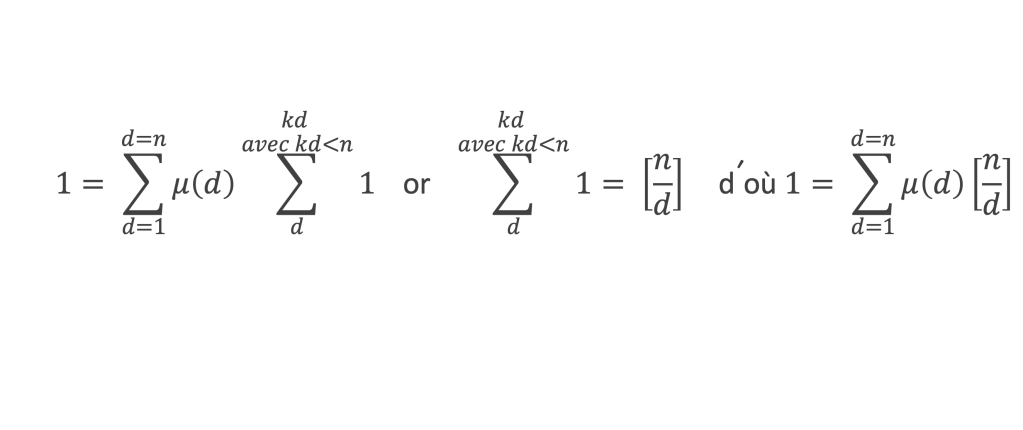
Par conséquent,

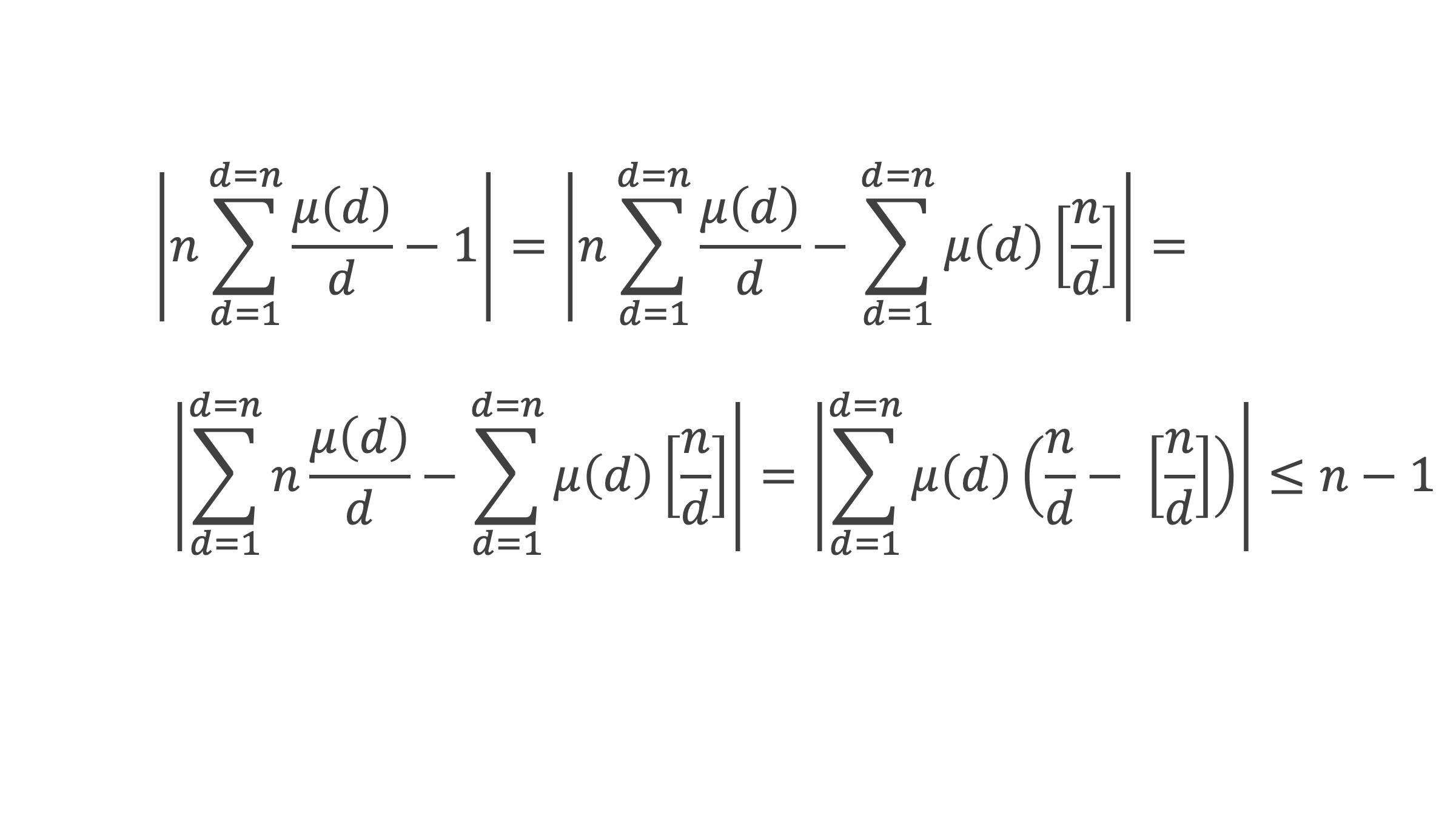
car la somme est constituée de n-1 termes inférieurs à 1 (et le dernier terme est nul).

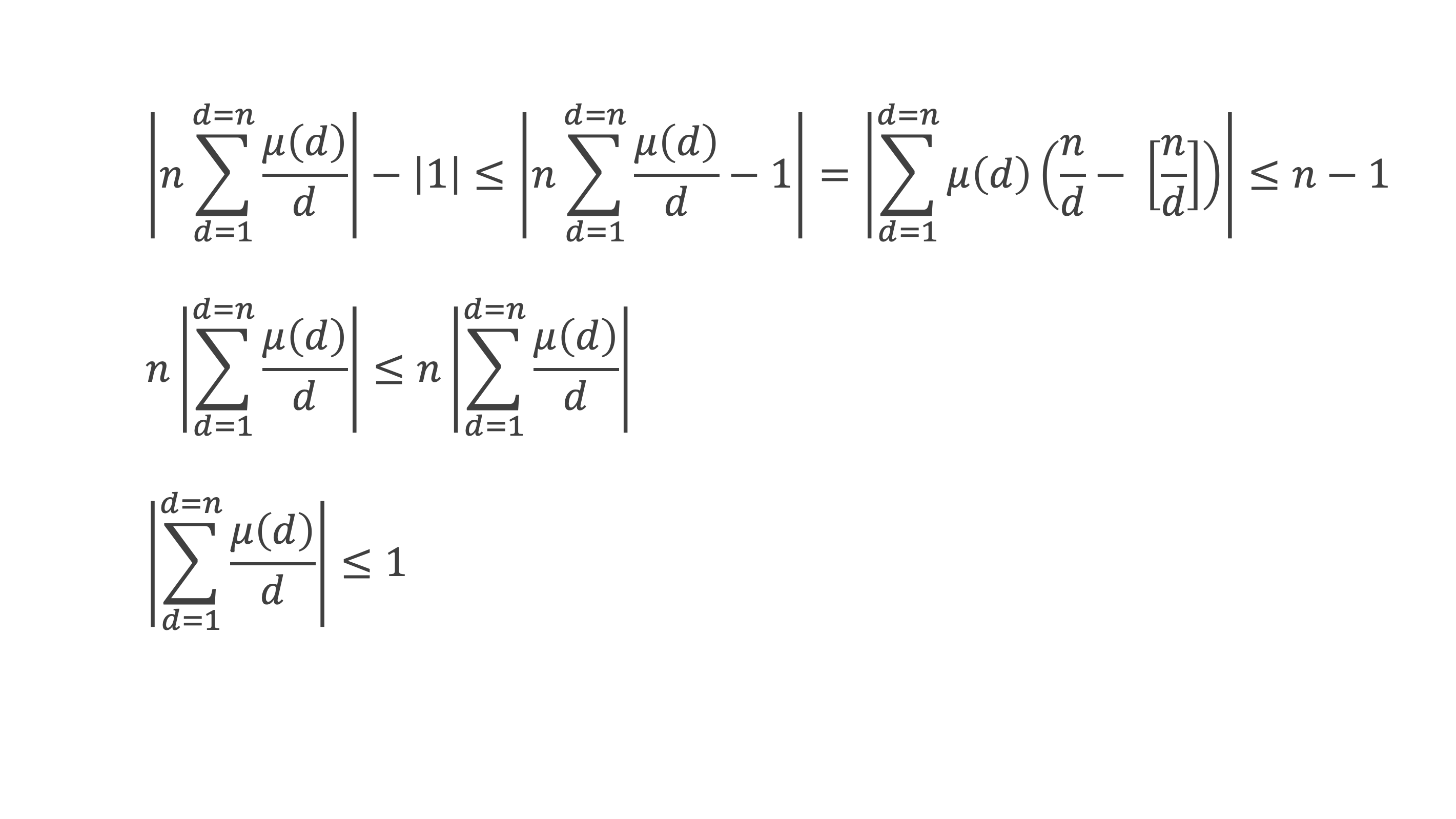
9- Lemme 8 : Le lemme 8 comprend 2 assertions :

Assertion 1 : Il existe une constante C1 telle que la fonction ε(y) = ∑_n≤y 1/n – log y + C1 tende vers 0 lorsque y -> +∞, de manière assez rapide pour que ε(y) (log y) tende aussi vers 0 (ce qui est une autre façon de dire que ε(y) tend plus vite vers 0 que log y ne tend vers l’infini, de sorte que le produit tend vers 0, c’est-à-dire finalement que ε(y) (log y) est un o(1) et que ε(y) est un o(1/log y)).

Assertion 2 : ∑_n≤y (log n)/n – 1/2 (log y)² tend vers une limite finie.

Démonstration de la première assertion :

Soit n la partie entière de y :

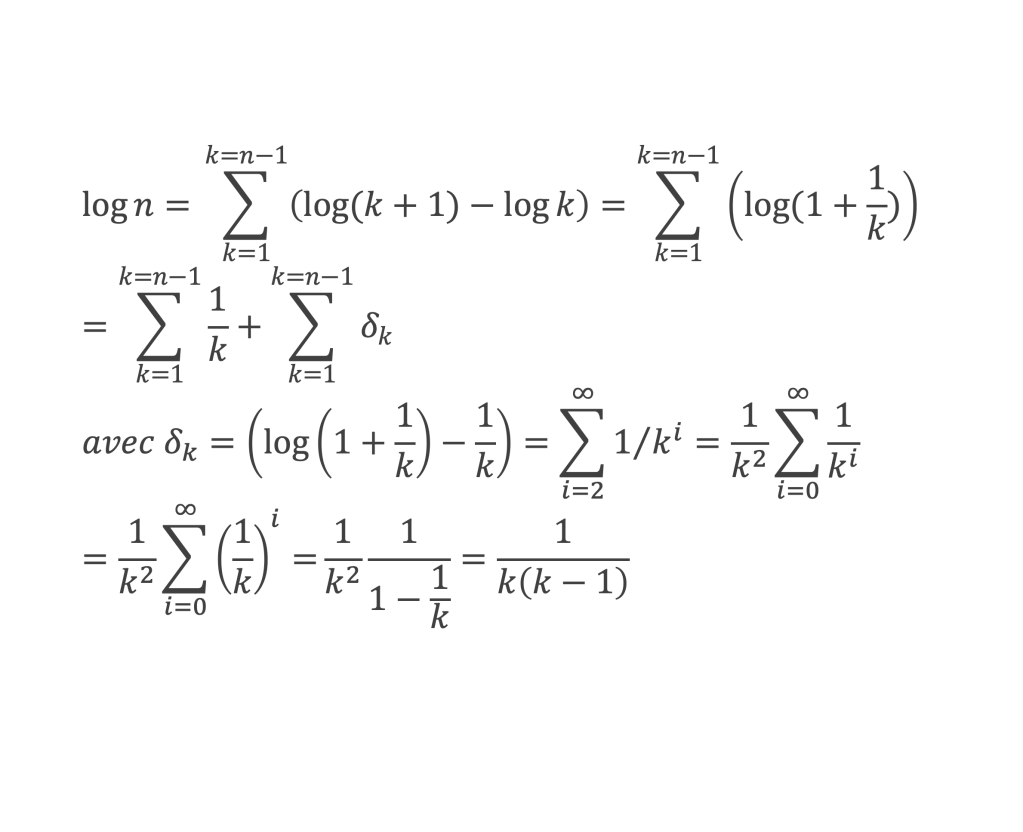
Pour chaque k > 2, il existe h tel que 2^h< k – 1 < 2^h+1, c’est-à-dire 1/2^h+1 < 1/(k – 1) < 1/2^h. Chaque tranche de 2^h à 2^h+1contient 2^h nombres, de sorte que :

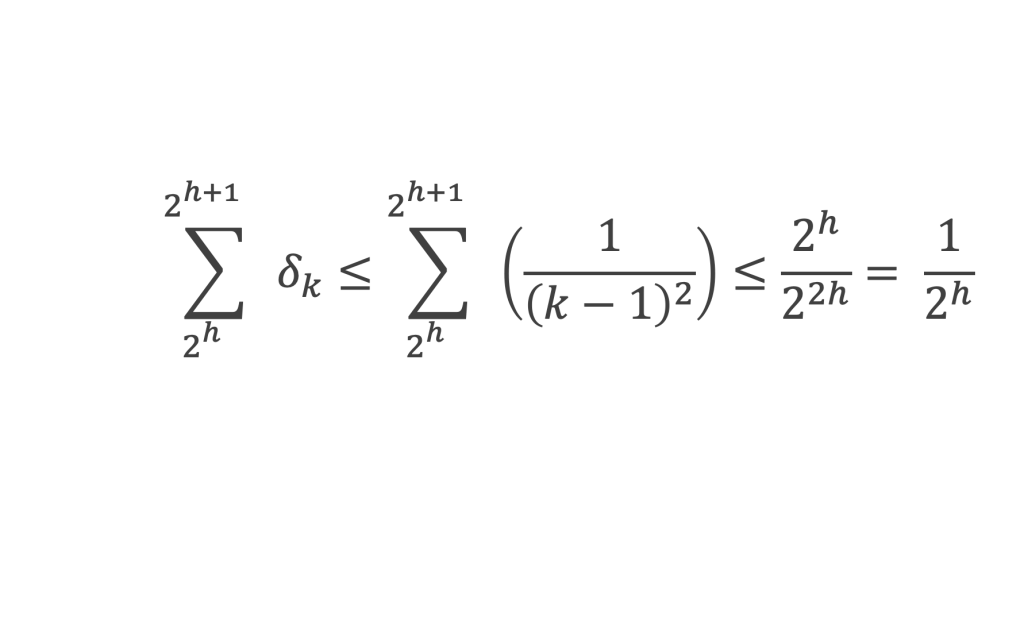
On en déduit :

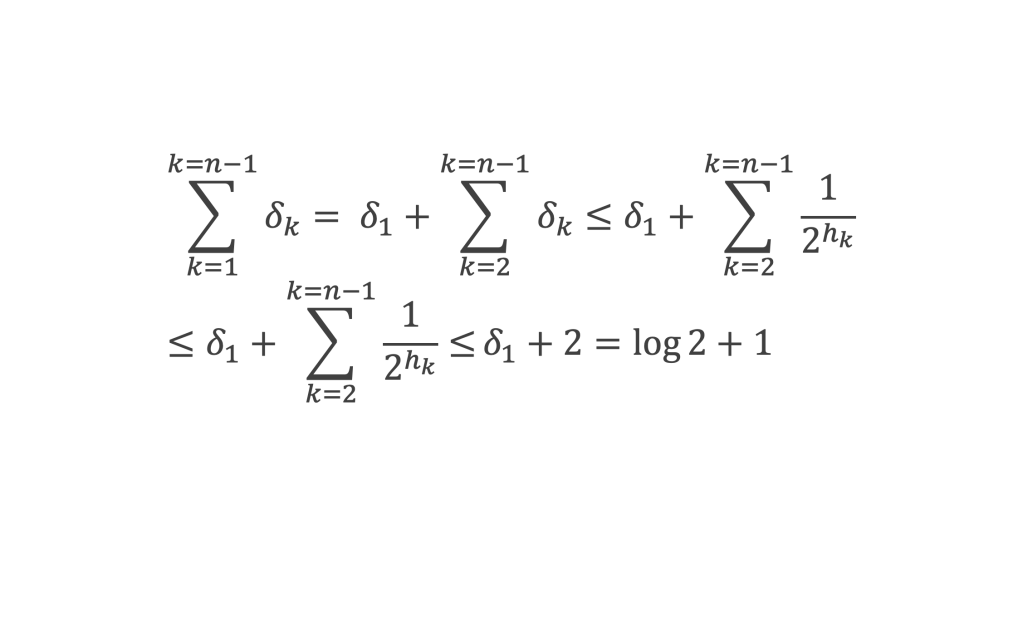
∑₁^n-1 δ_k converge donc vers une constante C1 < Log 2 + 1 lorsque n tend vers l’infini, et nous pouvons écrire :

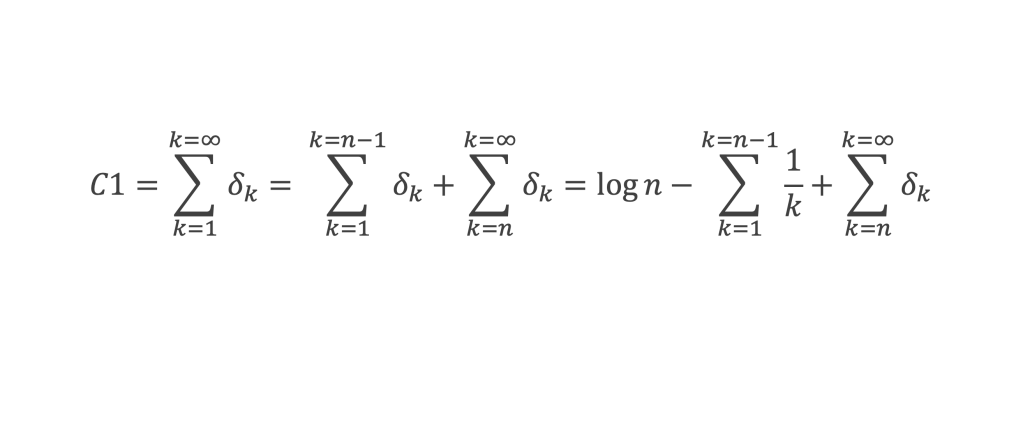
En posant ε_n(y) = ∑_n^∞ δ_k cela permet d’écrire : 

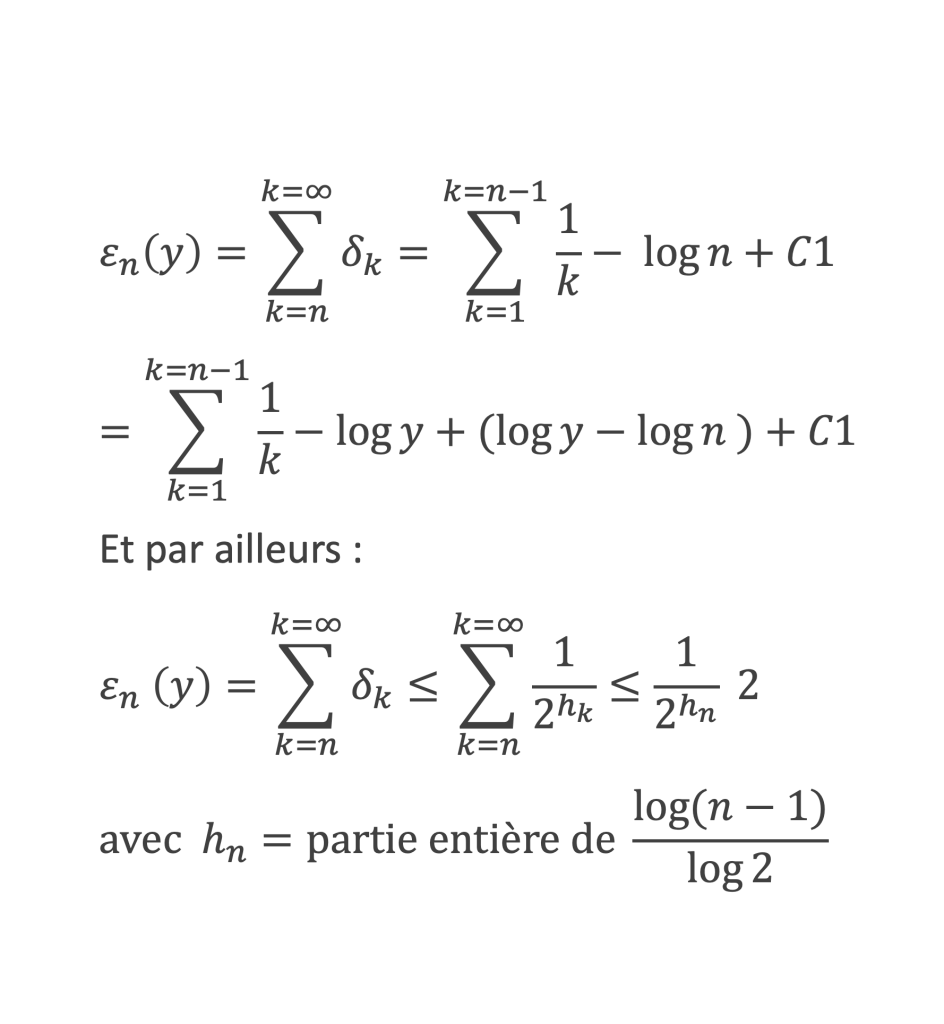
h_n + 1 est > partie entière de log(n – 1)/log 2. D’où :

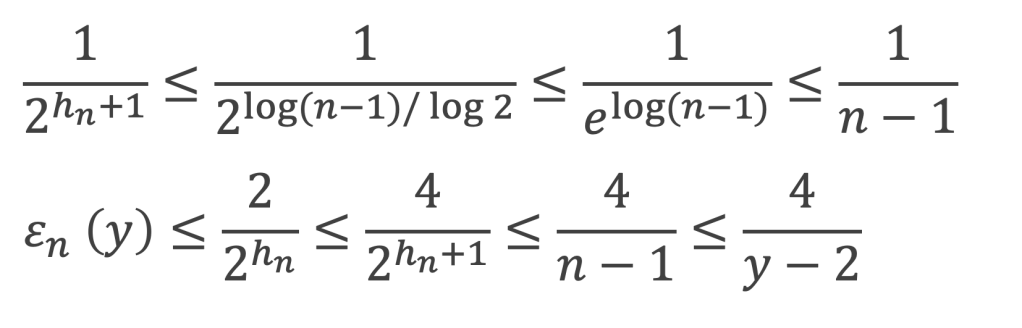
Par définition, ε(y) = ∑_n<y 1/n – log y + C1,

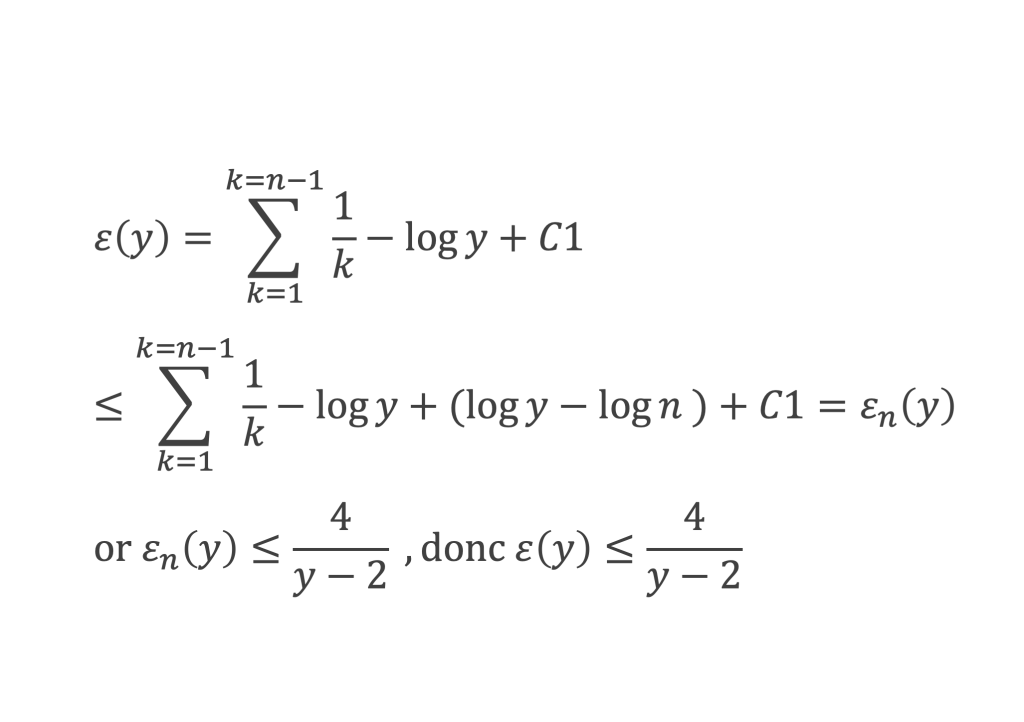
Donc lim ε(y) = 0 quand y -> +∞ , et de plus on a bien lim ε(y) log y = 0 quand y -> +∞ en vertu de lim log y / y = 0 quand y -> +∞. La première assertion du lemme est démontrée.

Démonstration de la seconde assertion : ∑_{n ≤ y} (log n)/n – 1/2 (log y)² tend vers une limite finie.

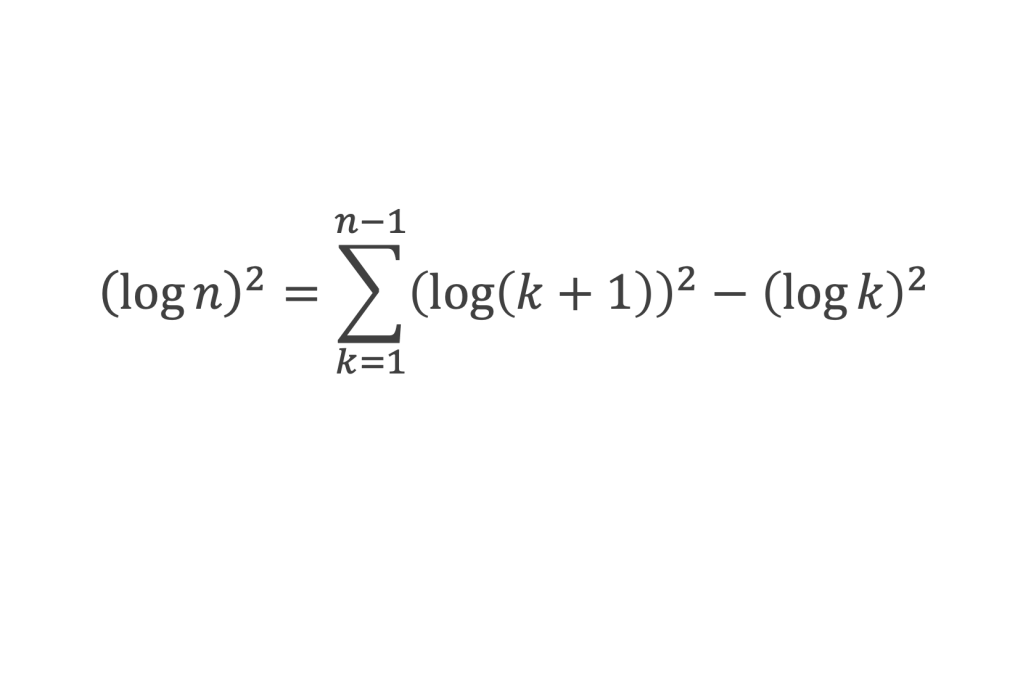
Or comme on l’a vu lors de la démonstration de la première assertion, log(k+1) = log k +1/k + δ_k , d’où :

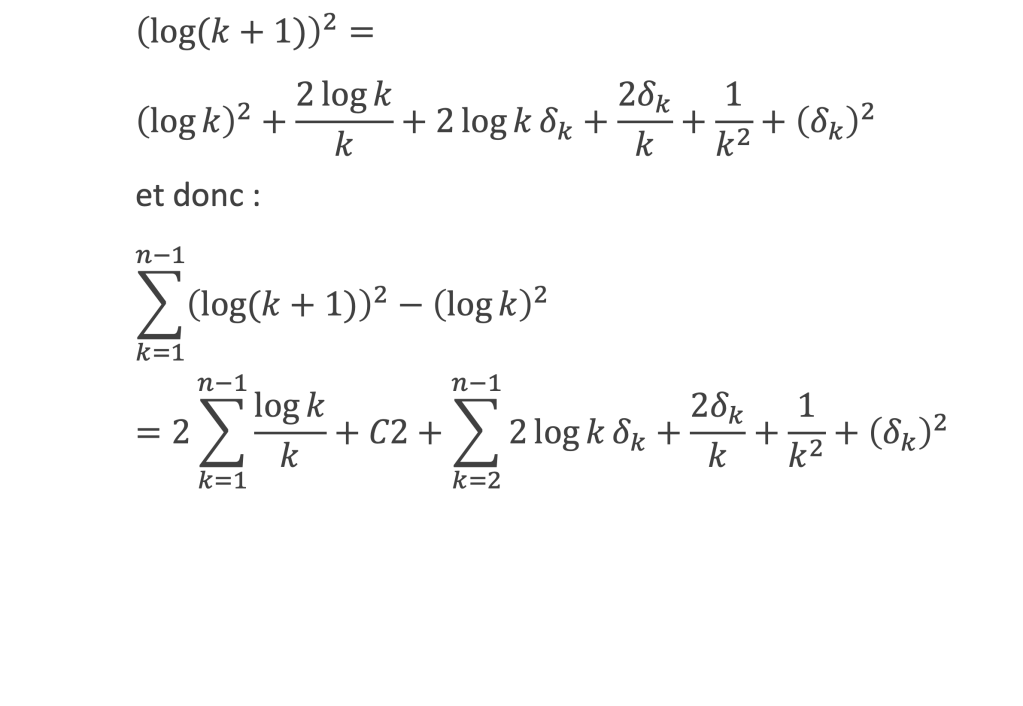
avec C2 correspondant au cas k = 1 de la seconde somme. La somme de gauche revient à (log n)² et en divisant le tout par 2 il vient :

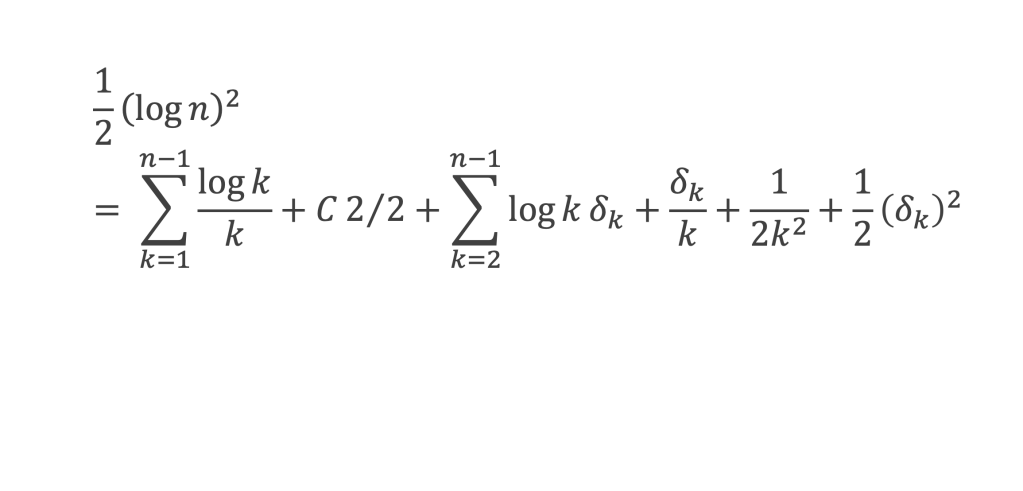
Comme δ_k ~ 1/k² la somme ∑₂^n-1 log k δ_k + δ_k/k + 1/2k² +1/2 (δ_k)² converge vers une constante C3 lorsque n tend vers l’infini, et en posant C4 = C2/2 + C3, nous pouvons écrire :

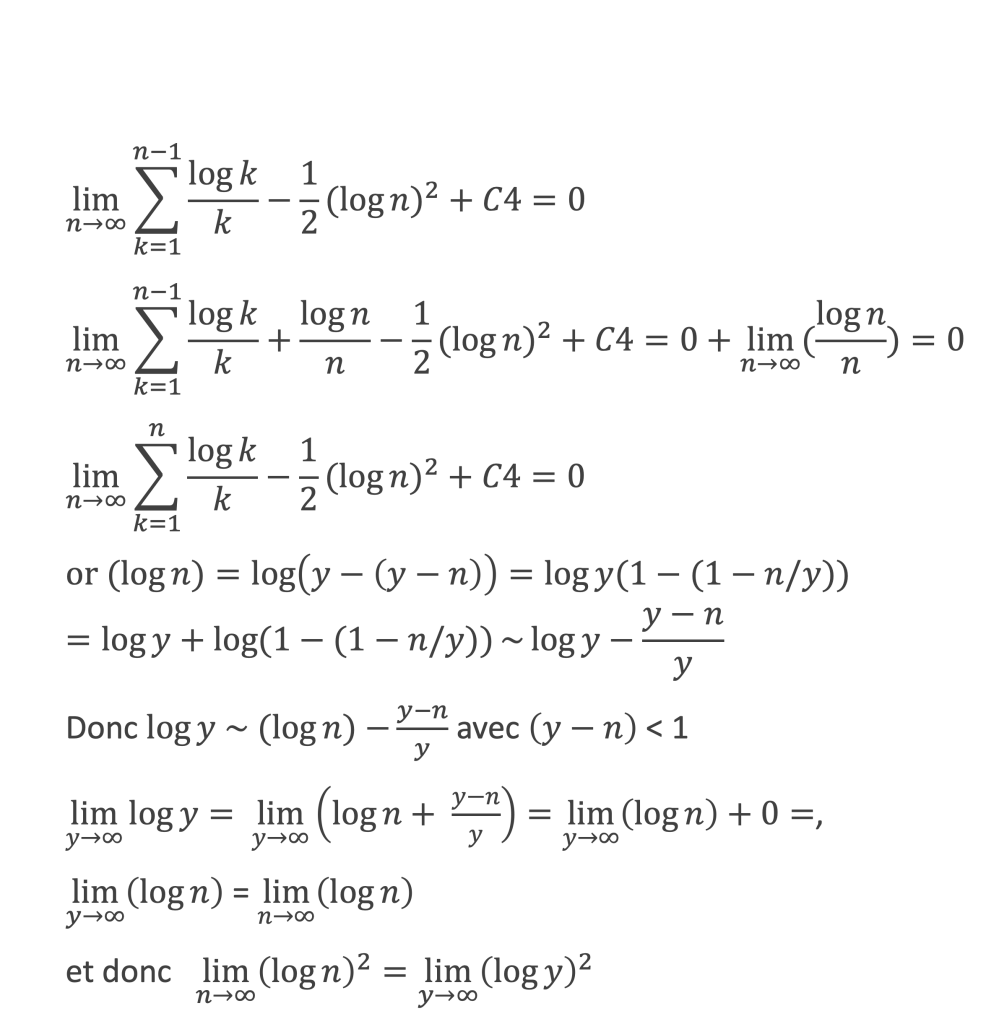
Ce qui permet de conclure que :

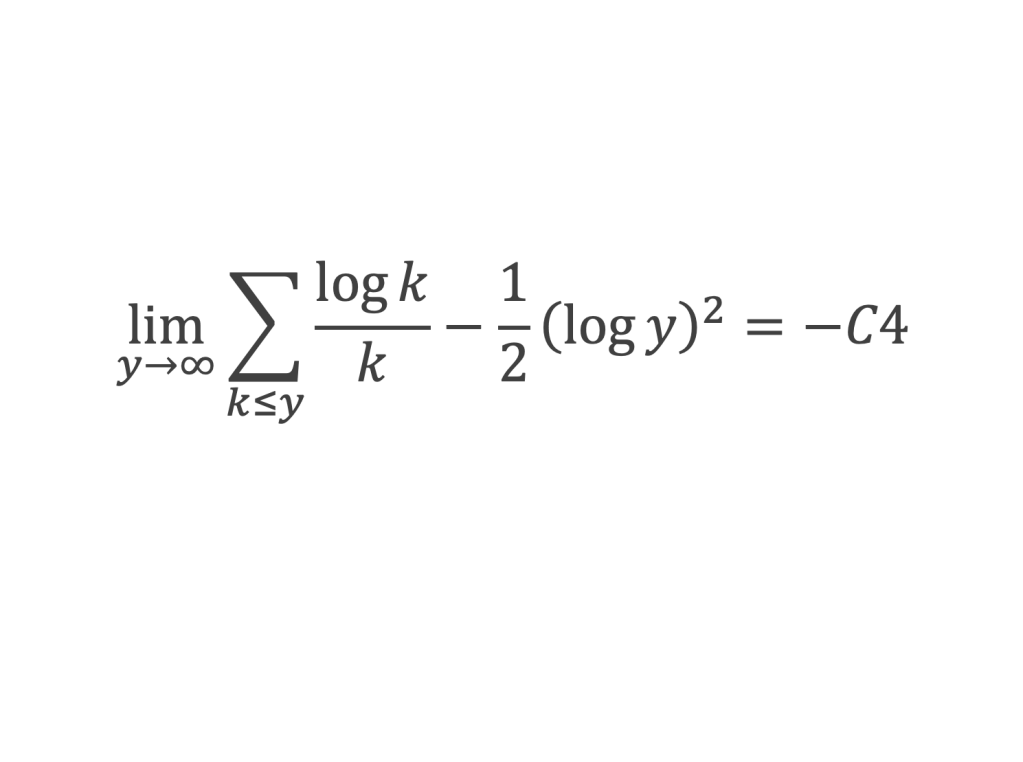
10- Lemme 9 : En désignant par τ(n) le nombre de diviseurs de n. On a :

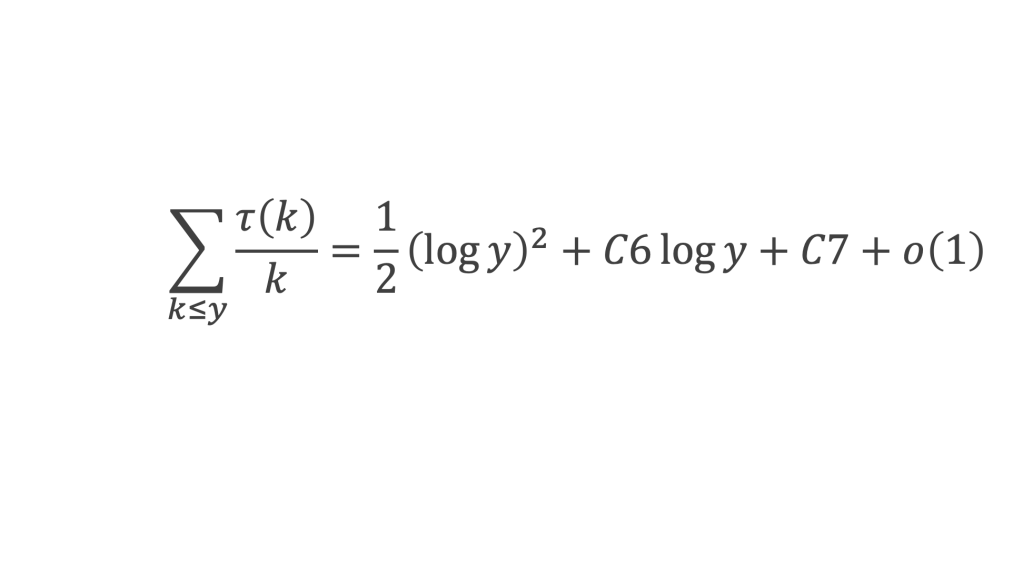
Où C6 et C7 sont des constantes, et o(1) une fonction qui tend vers 0 lorsque y tend vers l’infini.

Démonstration : τ(k) est le nombre de paires d’entier a, b, telles que le produit ab = k, donc :

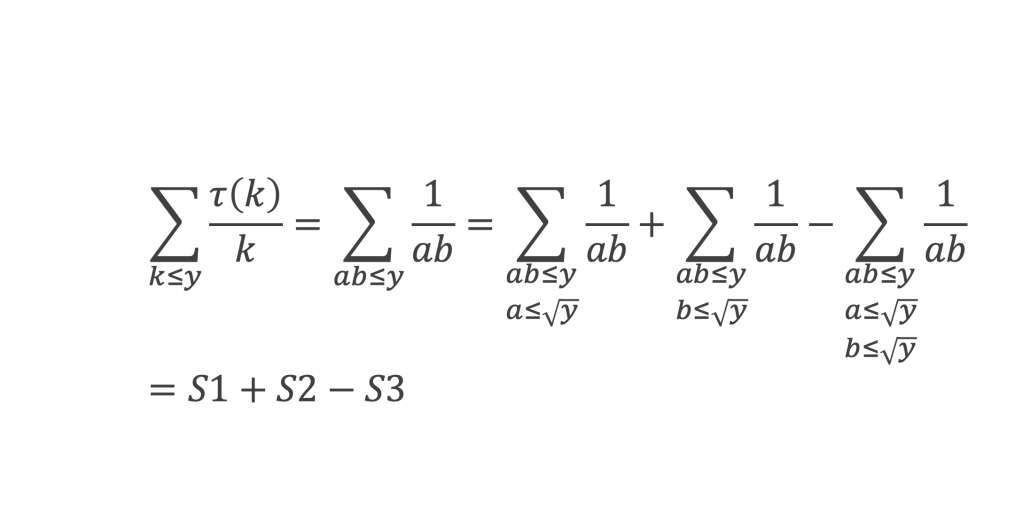
Cette somme comprend 3 termes : S1, S2, S3. Les 2 premiers S1 et S2 donneront des valeurs identiques, et la dernière somme S3 revient à :

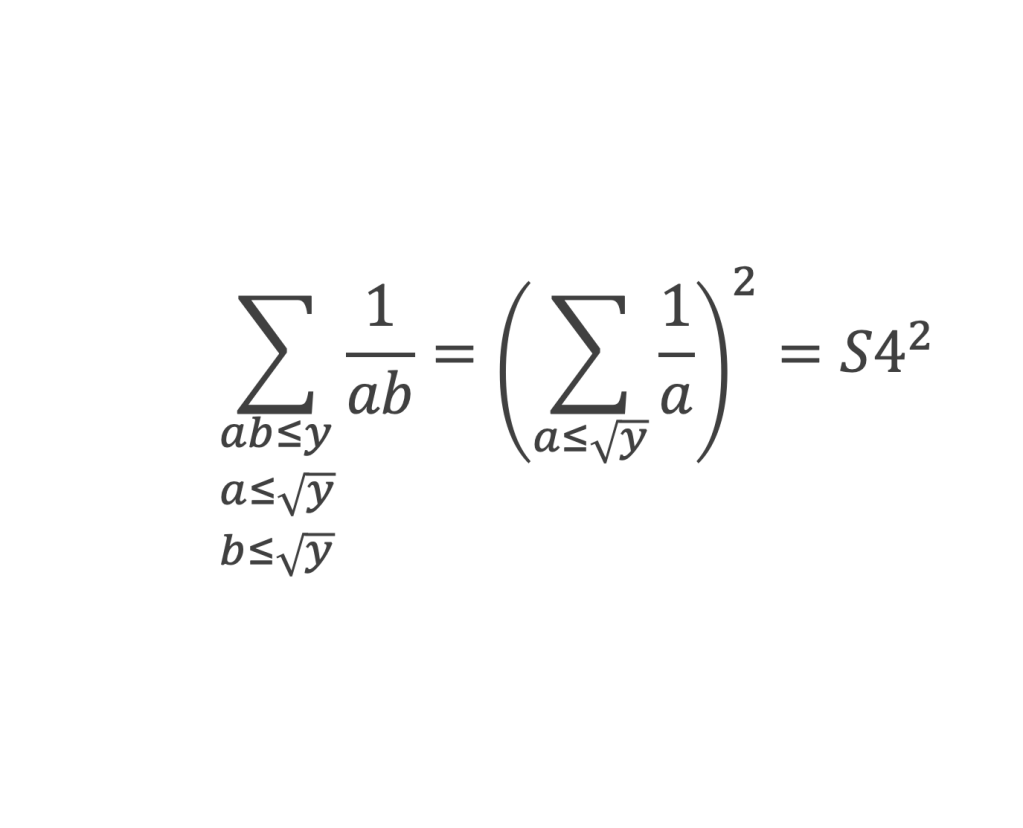
Calculons d’abord la somme S4. D’après la première assertion du lemme 8,  ∑_n<y 1/n = log y – C1 + ε(y) donc :

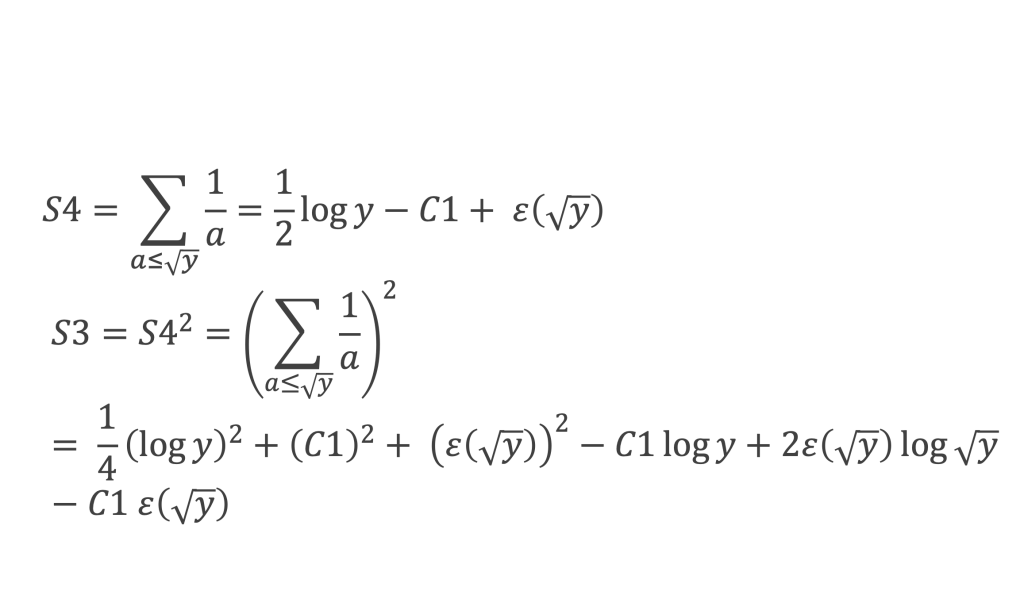
Les 3 termes contenant ε(√y) sont tous les trois des o(1), y compris celui multiplié par (log y) d’après la deuxième assertion du lemme 8, donc :

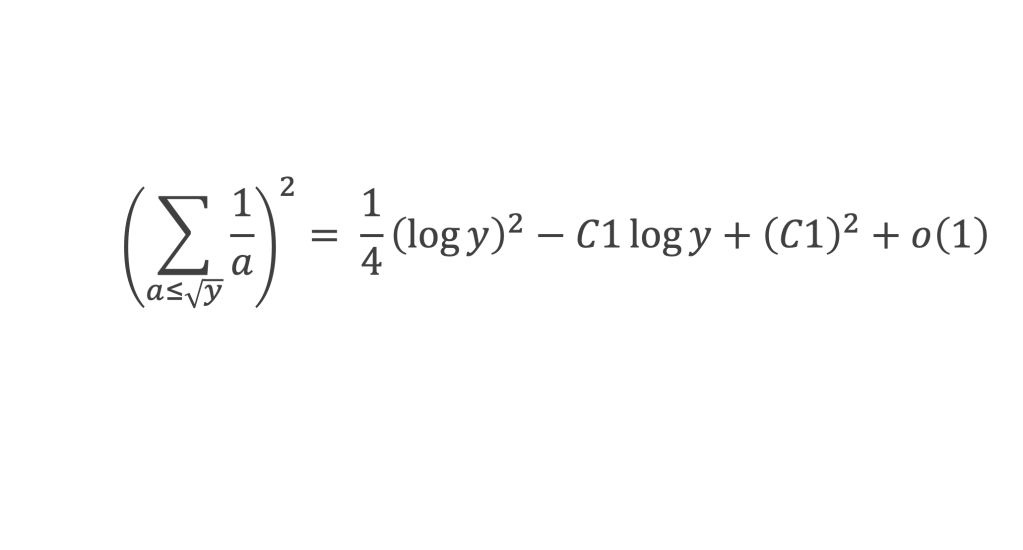
Calculons maintenant S1 (qui est aussi S2) : 

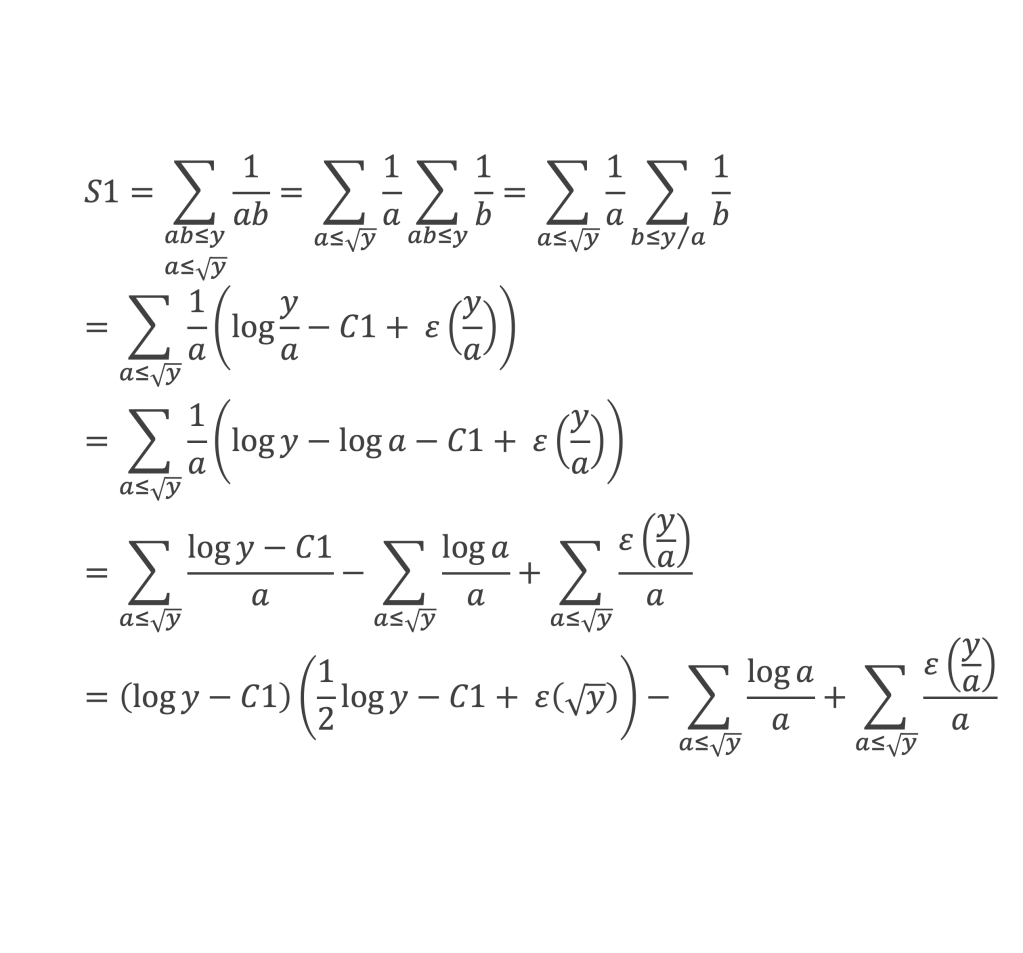
D’après la deuxième assertion du lemme 8, ∑_n≤y (log n)/n – 1/2 (log y)² tend vers une limite finie, donc :

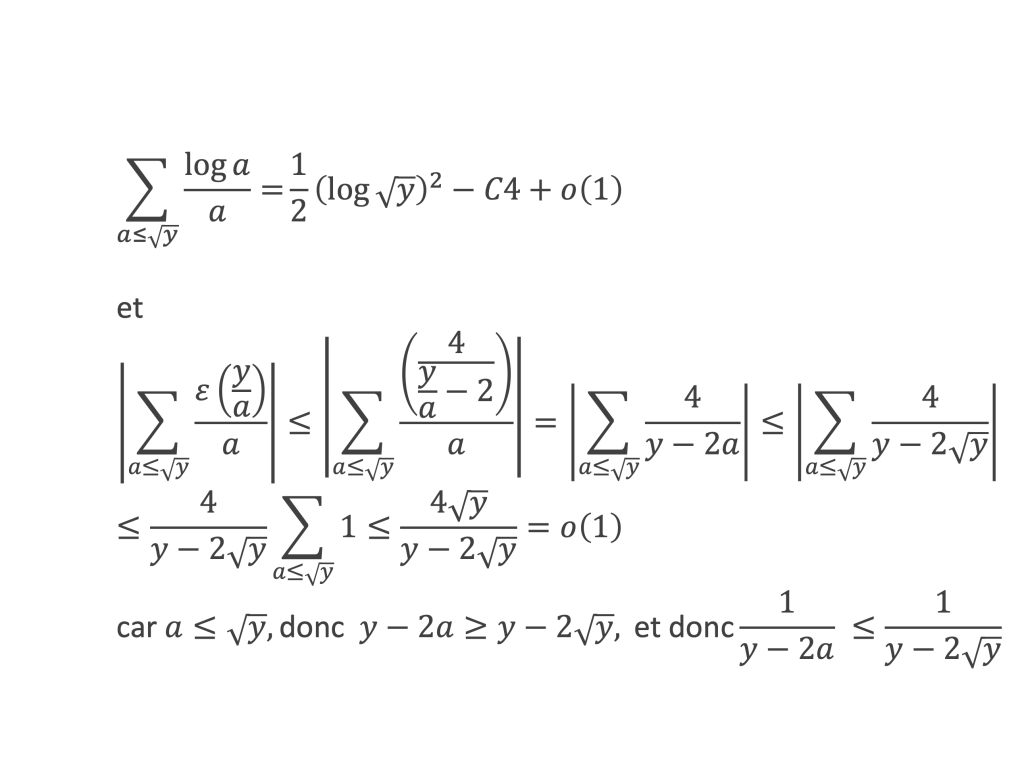
La somme S1 revient donc à :

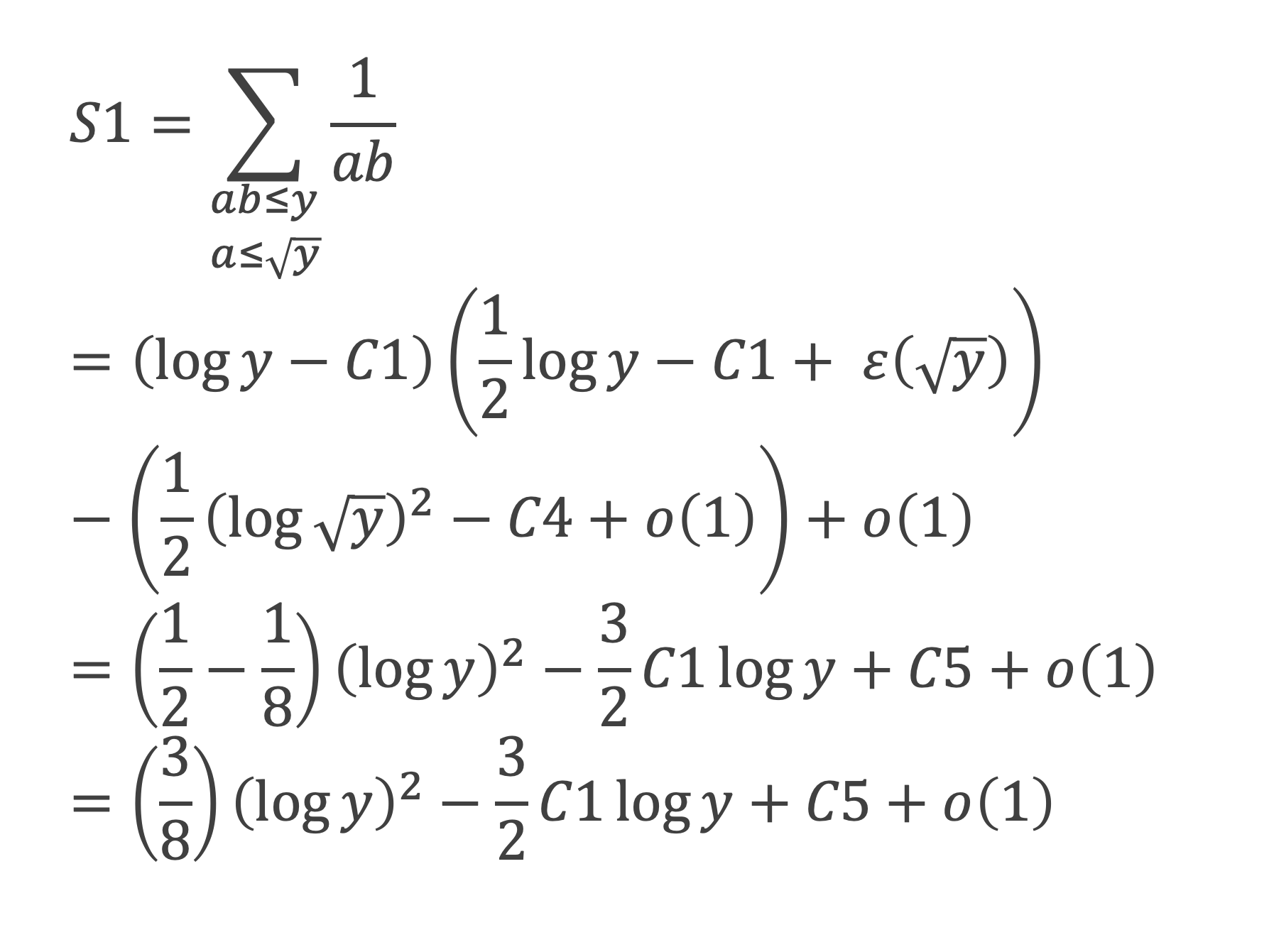
On en déduit, en regroupant les expressions de S1, S2 et S3 :

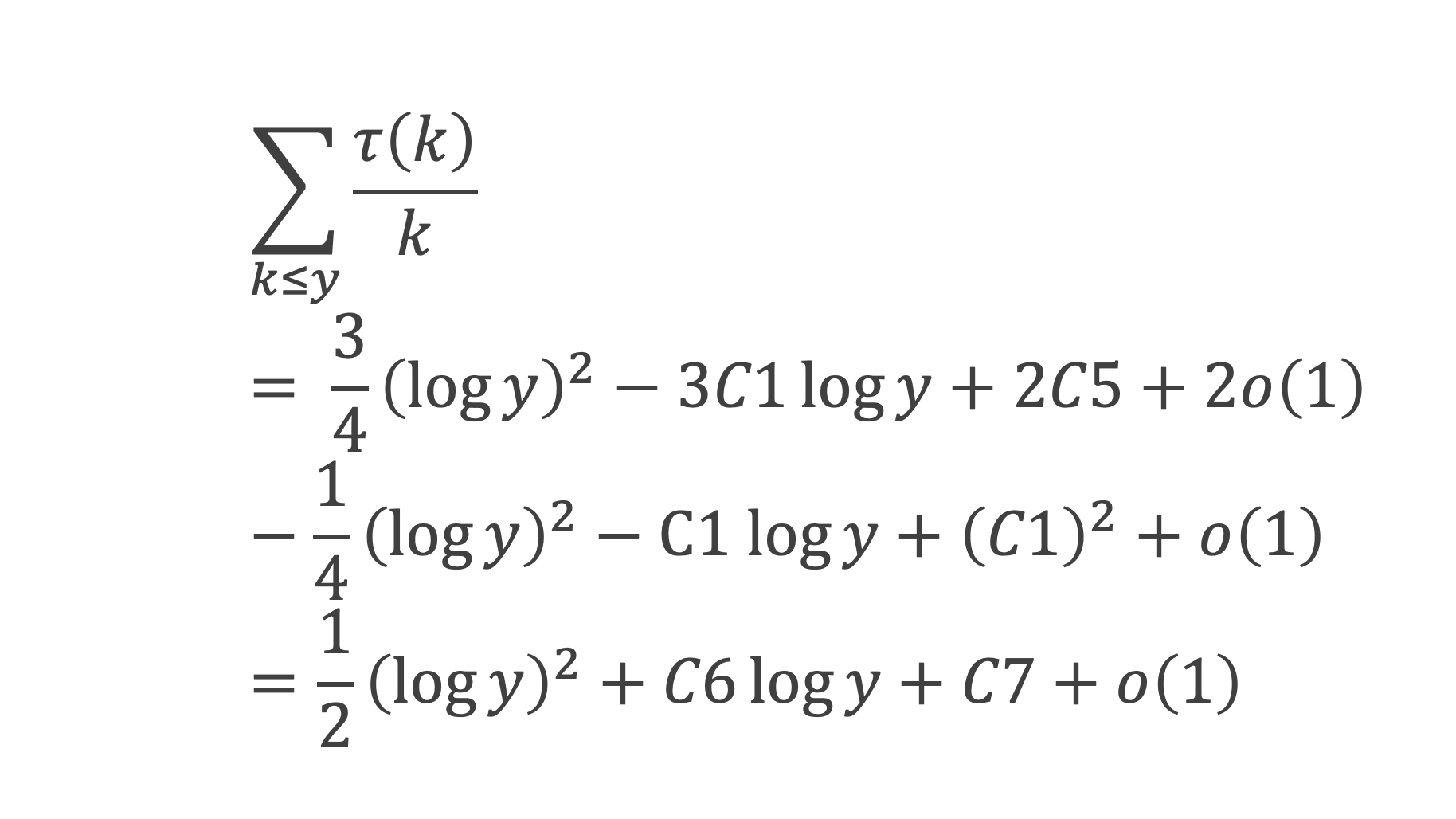
11- Lemme 10 : On a :

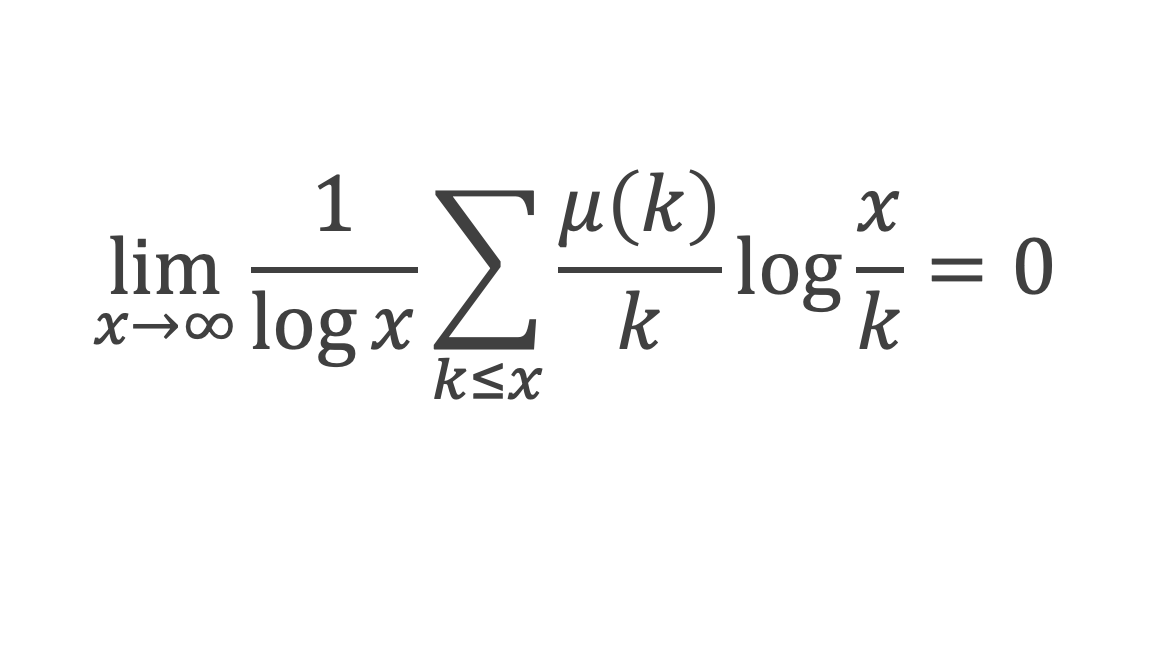
Autrement dit : ∑_k≤x μ(k)/k log(x/k) est un o(log x).

Démonstration : d’après le lemme 8, ∑_n<y 1/n = log y – C1 + ε(y)

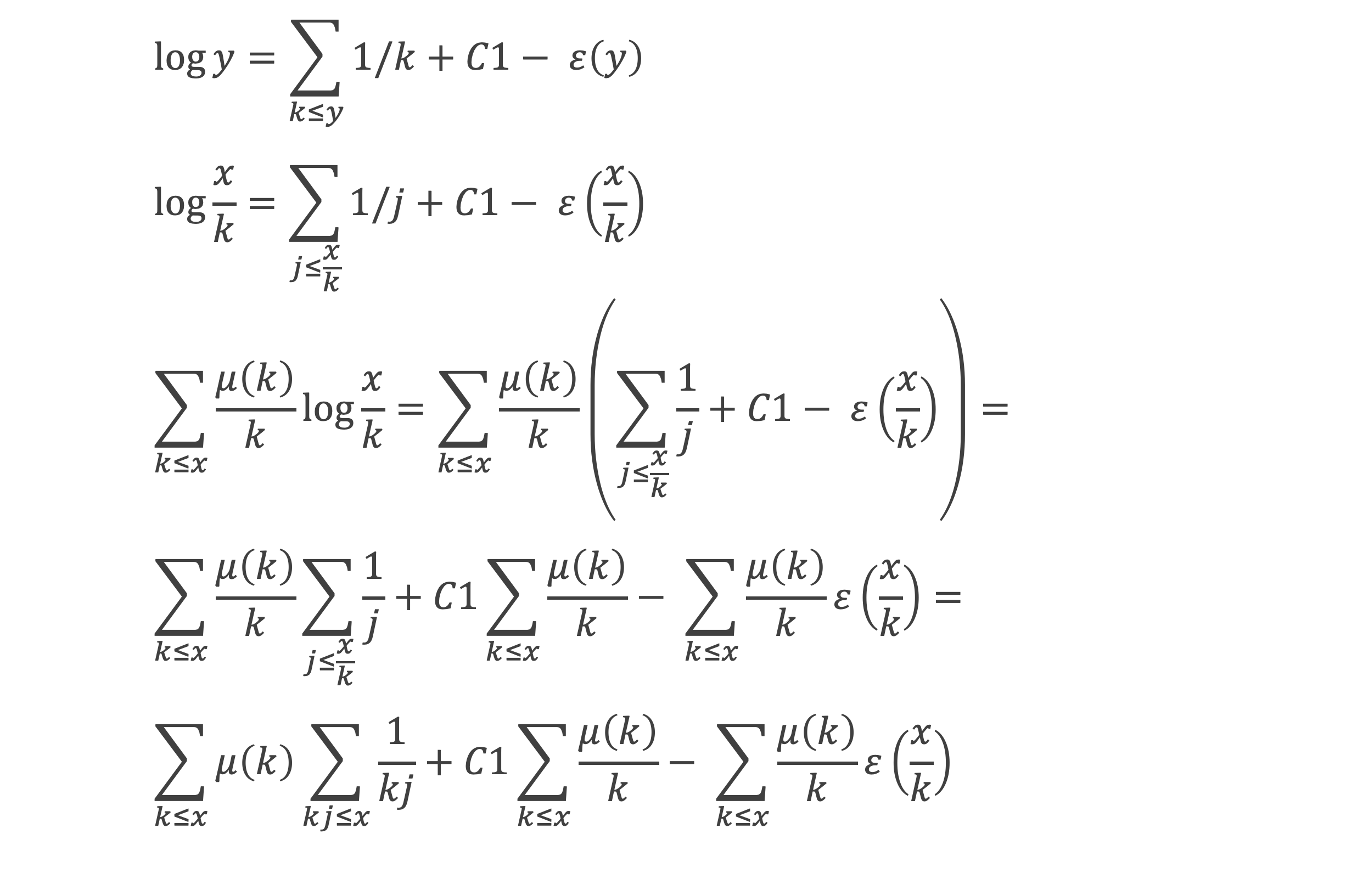
On pose m = j_*k. Chaque k est un diviseur de m. En regroupant la double somme par valeur de 1/(jk) identique , on peut écrire :

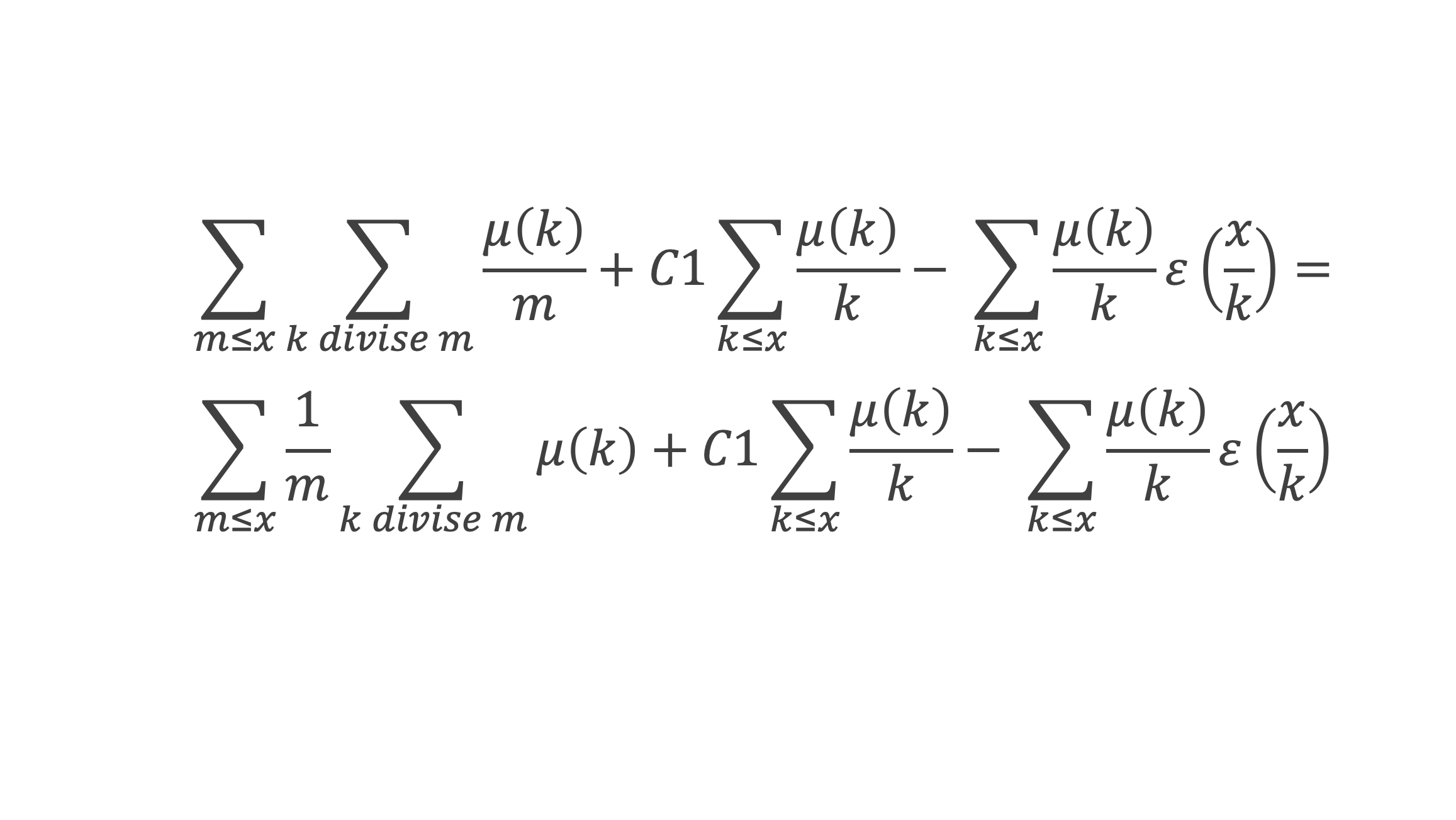
D’après le lemme 1, ∑_k/m μ(k) = 0 , sauf pour m = 1, auquel cas la somme vaut 1. Donc le terme ∑_m≤x1/m ∑_k/m μ(k) = 1.

D’après le lemme 7, la valeur absolue de ∑_k≤x μ(k)/k est ≤ 1

Il ne reste plus qu’à démontrer que ∑_k≤x μ(k)/k ε(x/k) est un o(log x). Pour cela nous pouvons déjà écrire :

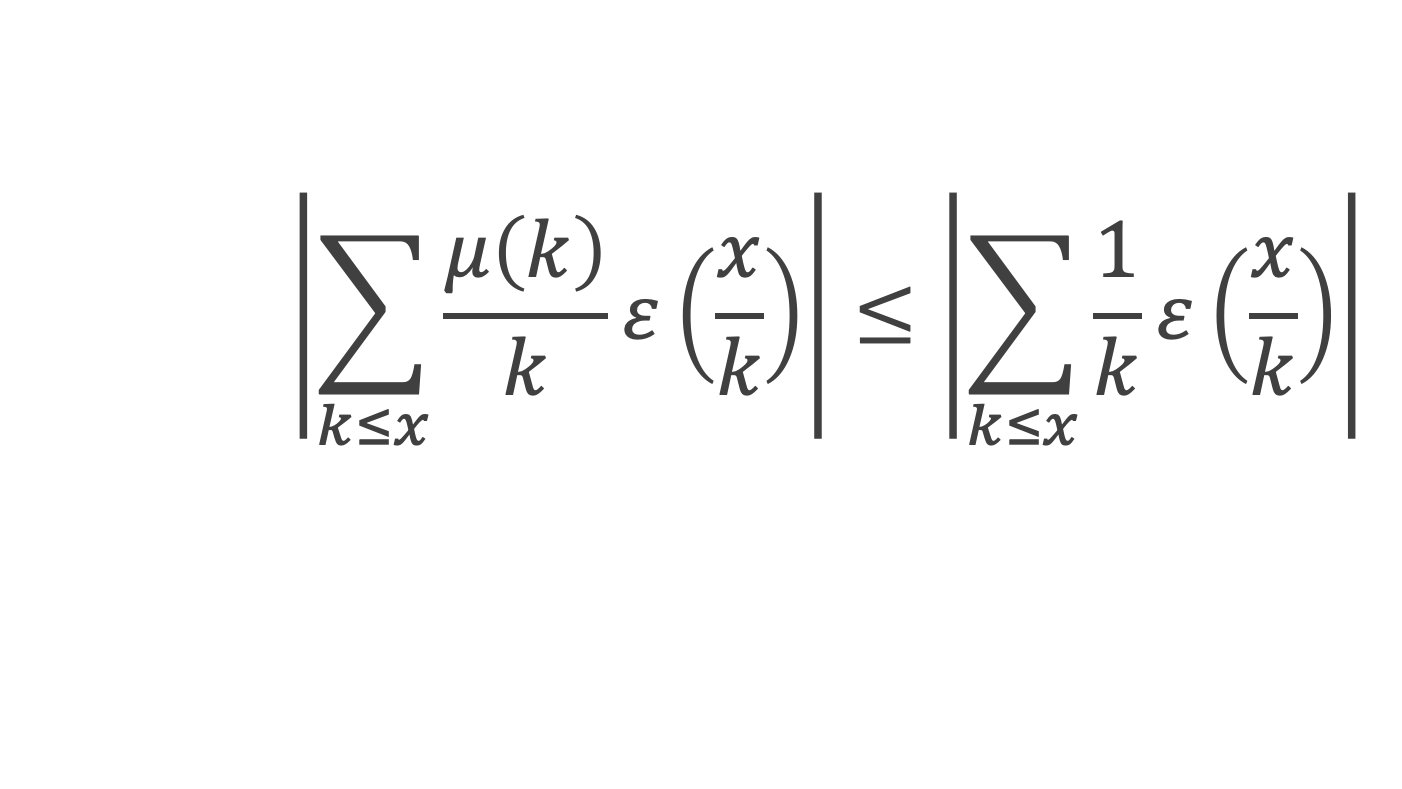
Soit y défini par y = x^1-ρ = x/x^ρ avec ρ = 1/√(log x).  On a y < x et pour tous les k < y on a : x/k > x/y = x^ρ  = exp(ρ logx) = exp( √(log x)). Par conséquent x/y tend vers l’infini lorsque x tend vers l’infini, et pour k < y on aura x/k qui tendra vers l’infini lorsque x tendra vers l’infini. On obtient donc ε(x/k) tend vers 0 quand x tend vers l’infini, ce qui signifie finalement que chaque ε(x/k) = o(1). Cela permet de conclure que la somme, étendue jusqu’à y est un o(log x) :

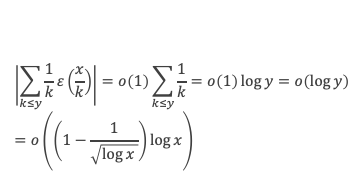
Par ailleurs la contribution des k compris entre y et x est aussi un o(log(x) :

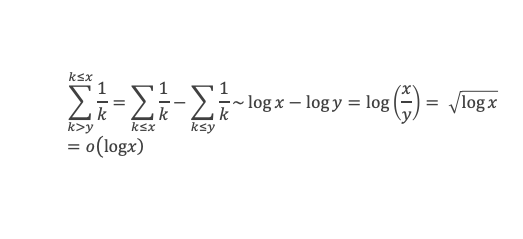
En conclusion, ∑_k<x μ(k)/k ε(x/k) est bien un o(log x). Le lemme est démontré.

12- Lemme 11 : Pour chaque entier n, on a :

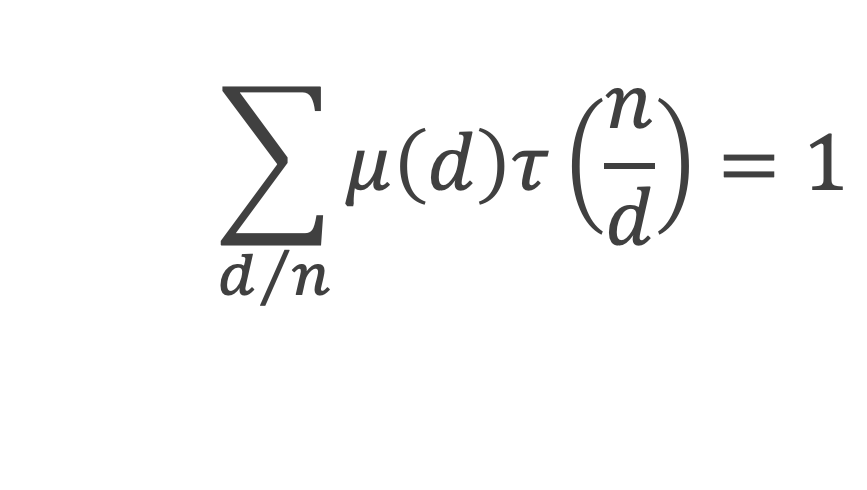
Démonstration : τ(m) étant le nombre de diviseurs de m, et d1 les diviseurs de m, On se rappelle que τ(m) = ∑_d1/m1 . D’où :

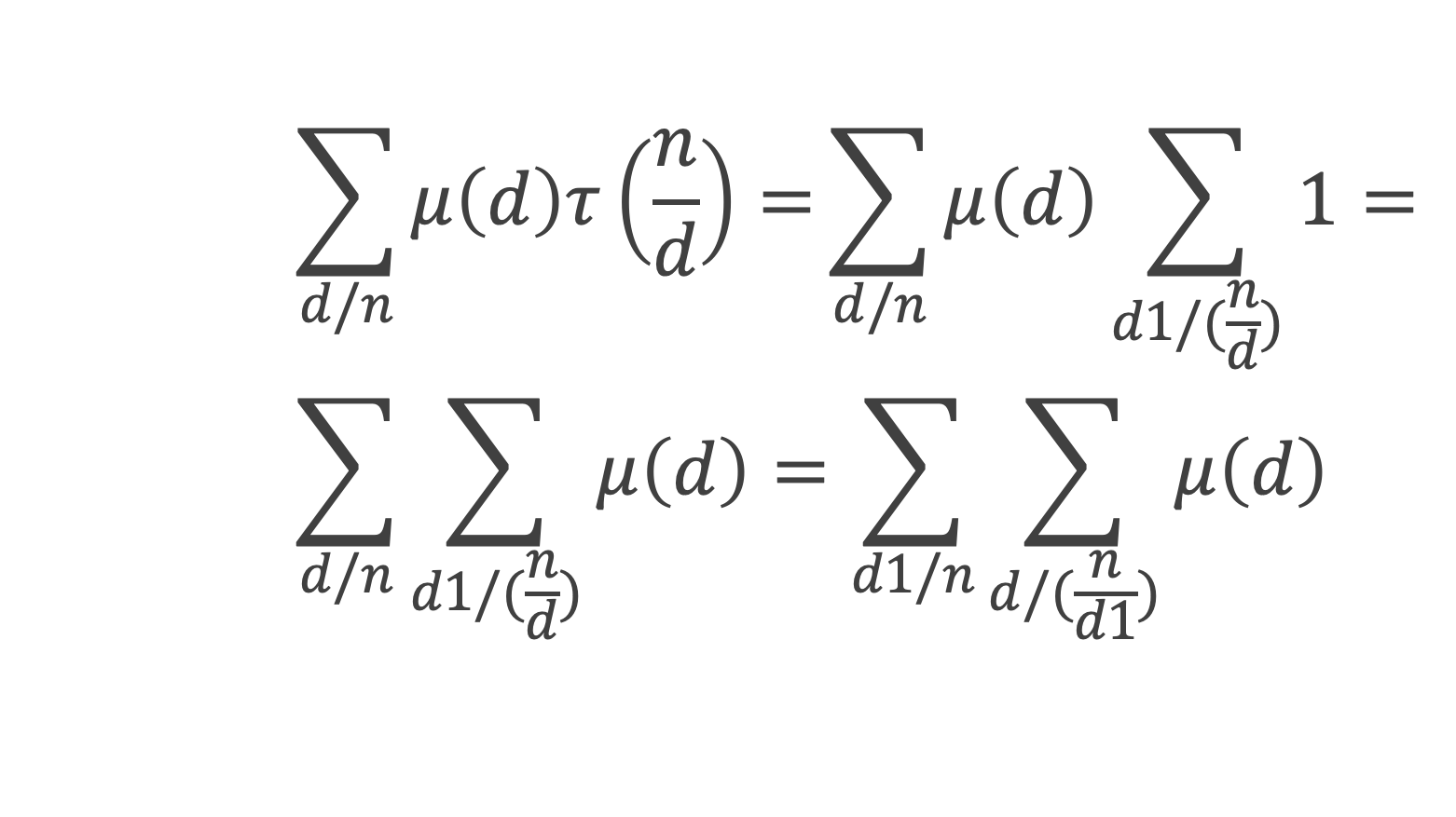
Pour d1 < n, la somme des μ(d) pour d diviseur de n/d1 = 0 lorsque n/d1 > 1, d’après le lemme 1. La seule contribution non nulle est celle pour d1 = n, et dans ce cas elle vaut 1, d’où le lemme.

13- Lemme 12 : 

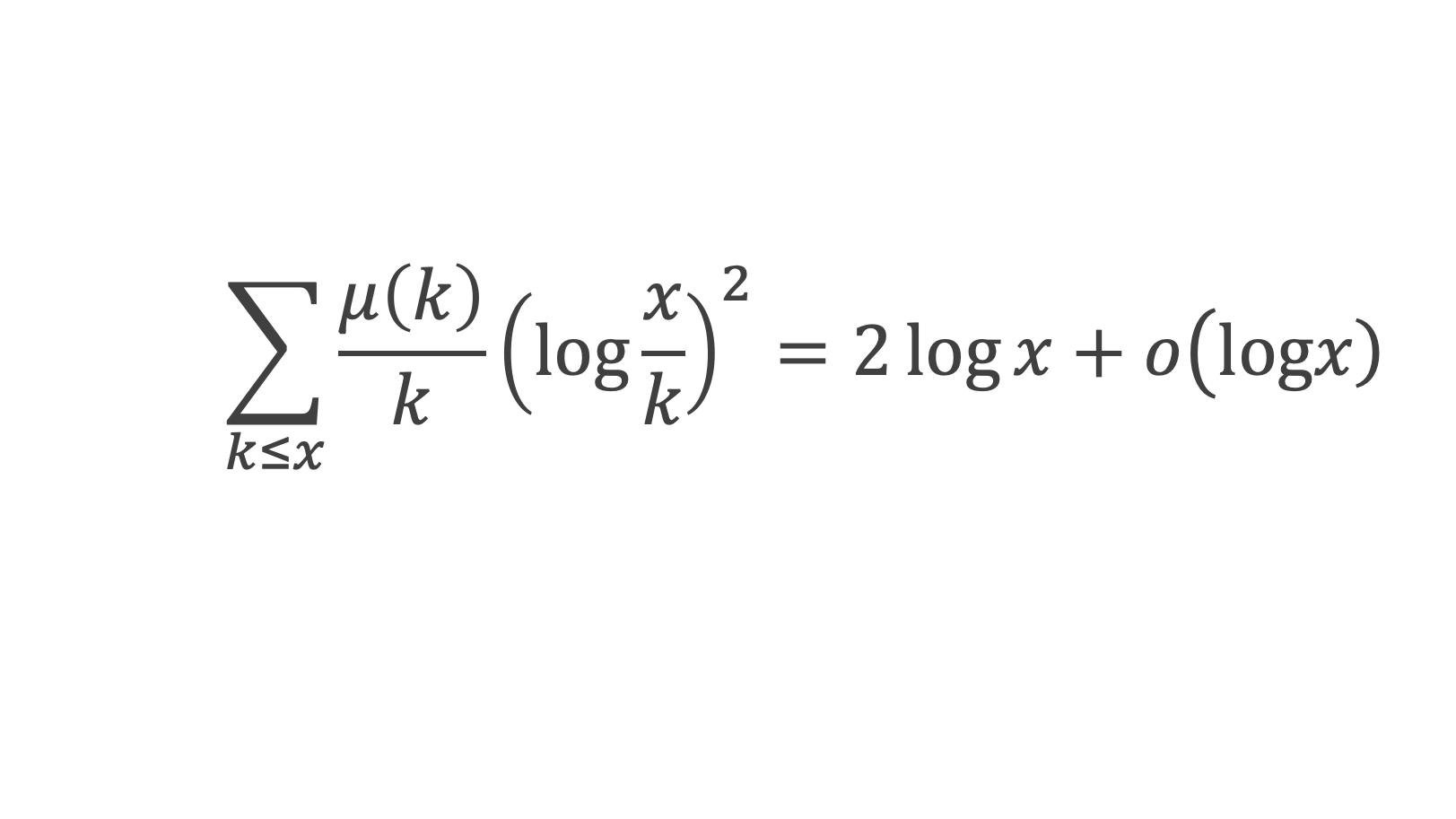
Démonstration : D’après le lemme 9, 

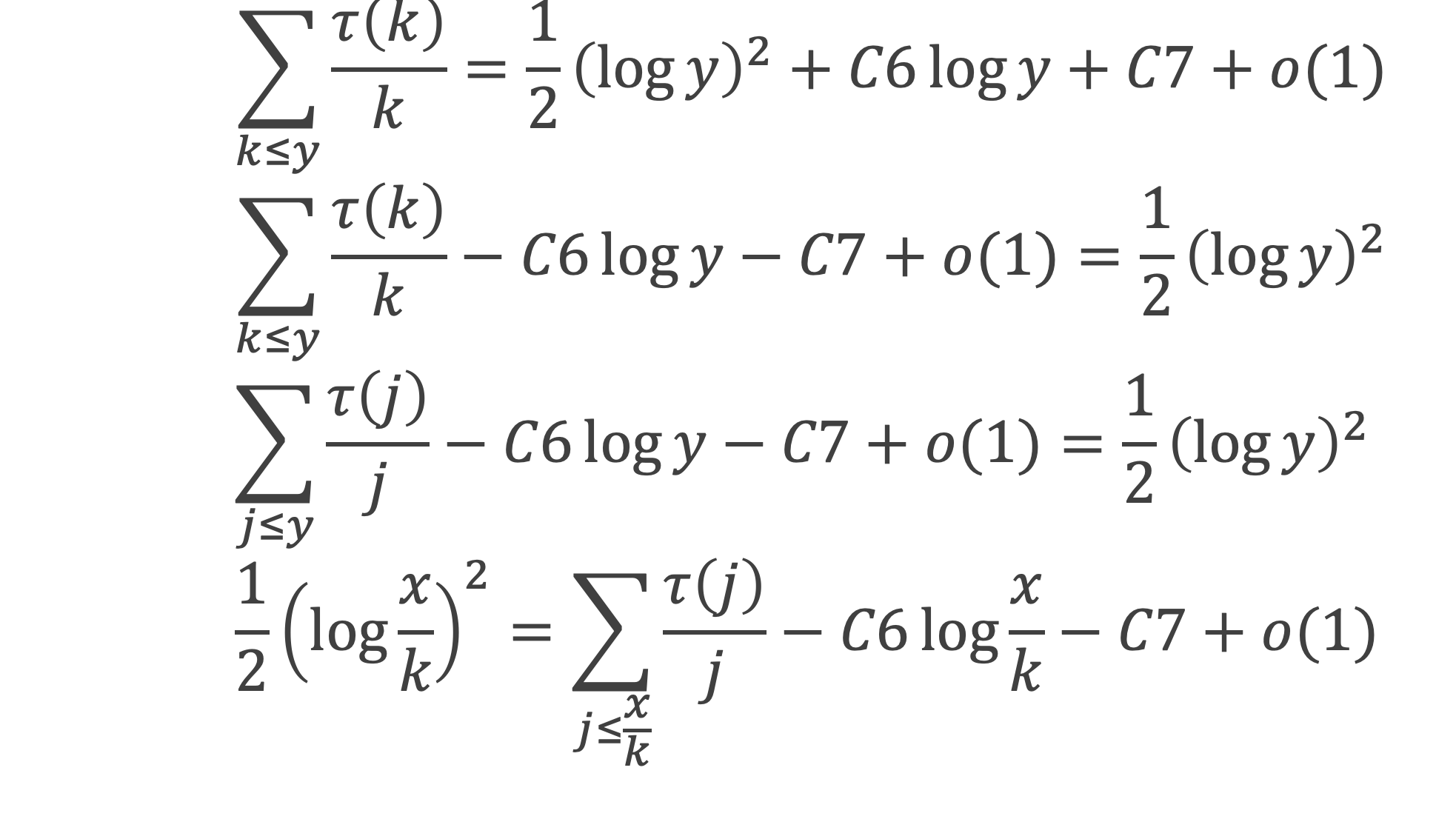
Ce qui permet d’écrire :

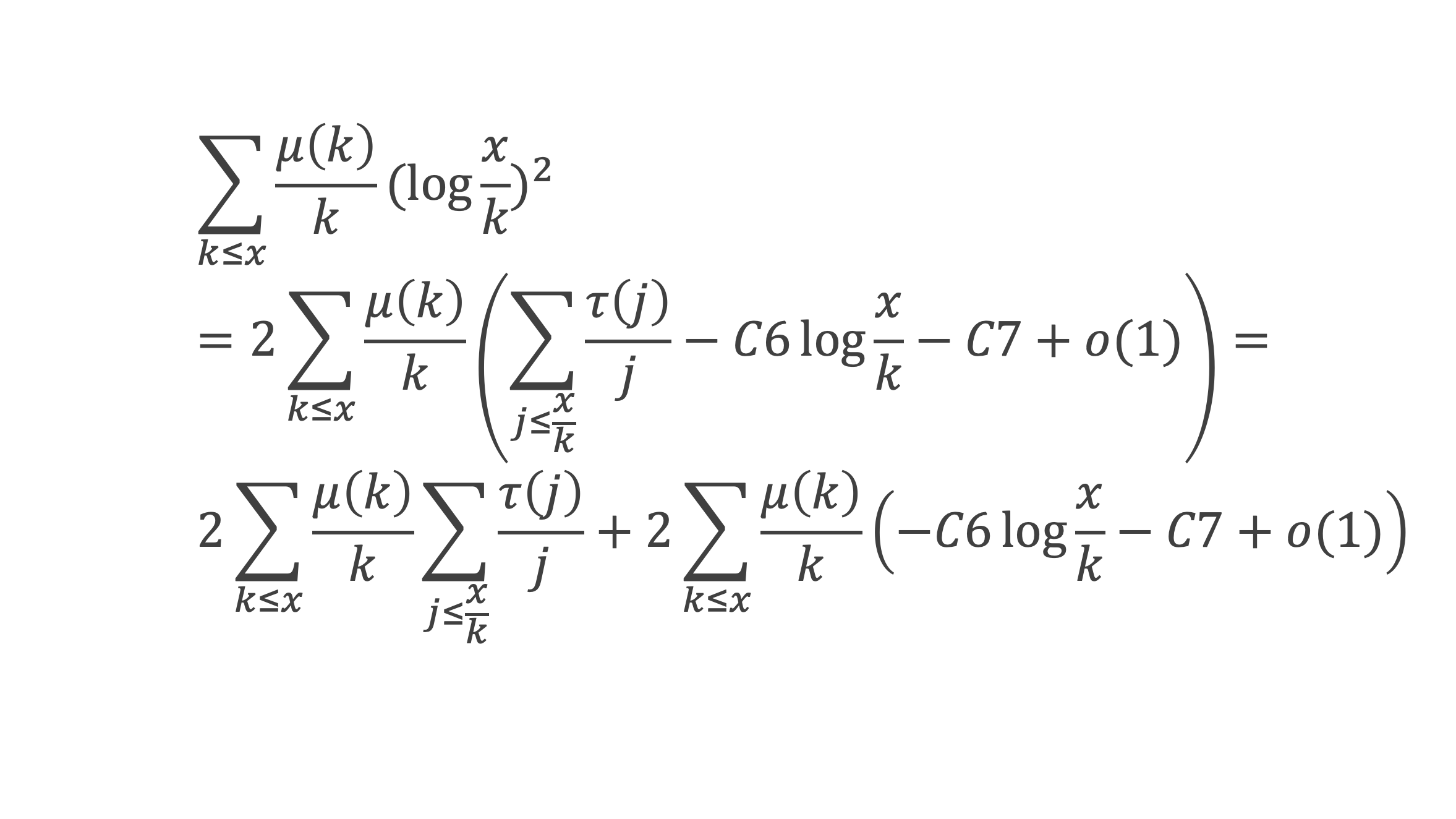
D’après le lemme 10, ∑_k<x μ(k)/k log(x/k) est un o(log x), et d’après le lemme 7,  ∑_k≤x μ(k)/k est compris entre -1 et +1. On en déduit :

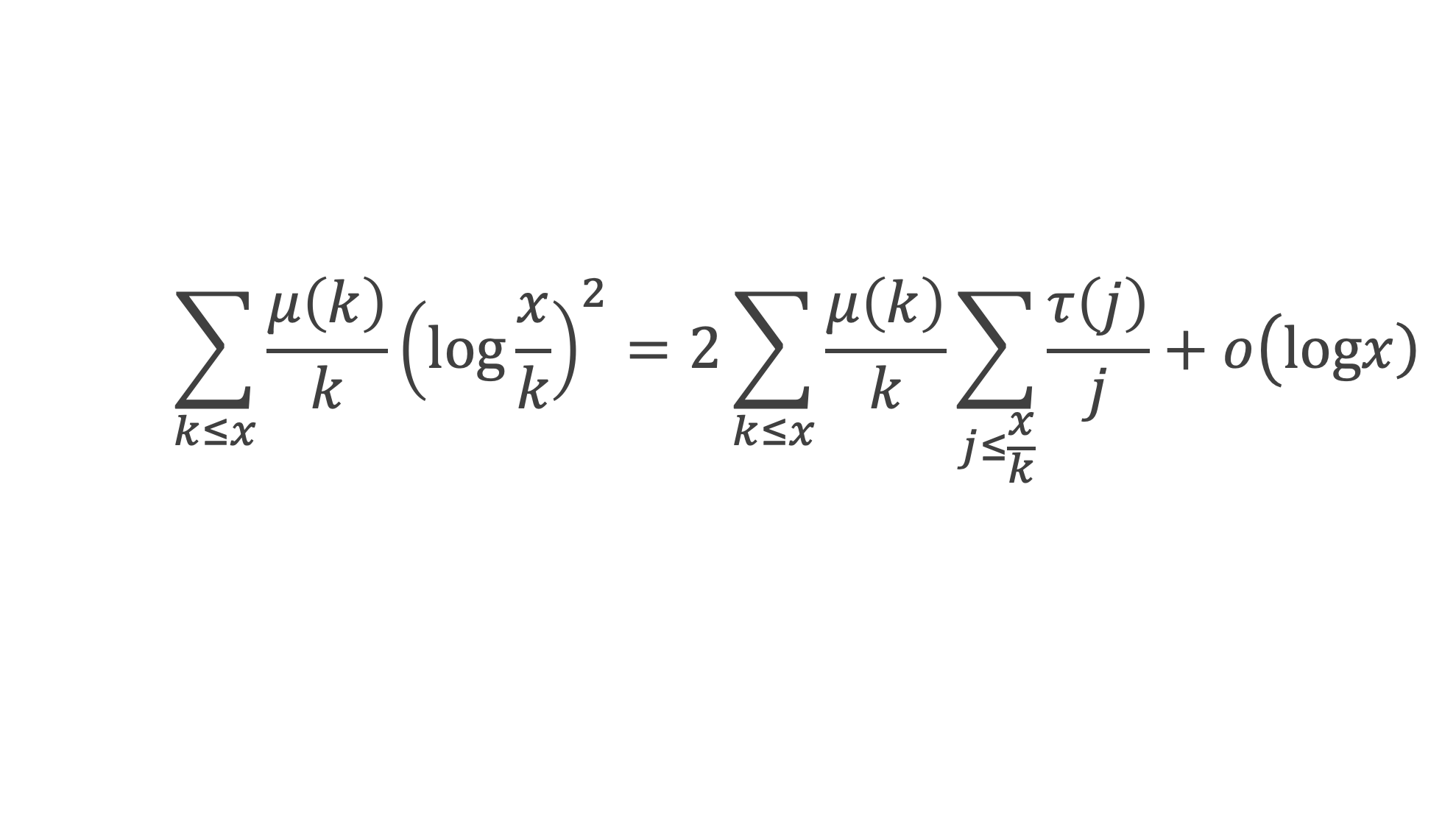
Posons n = j_*k.

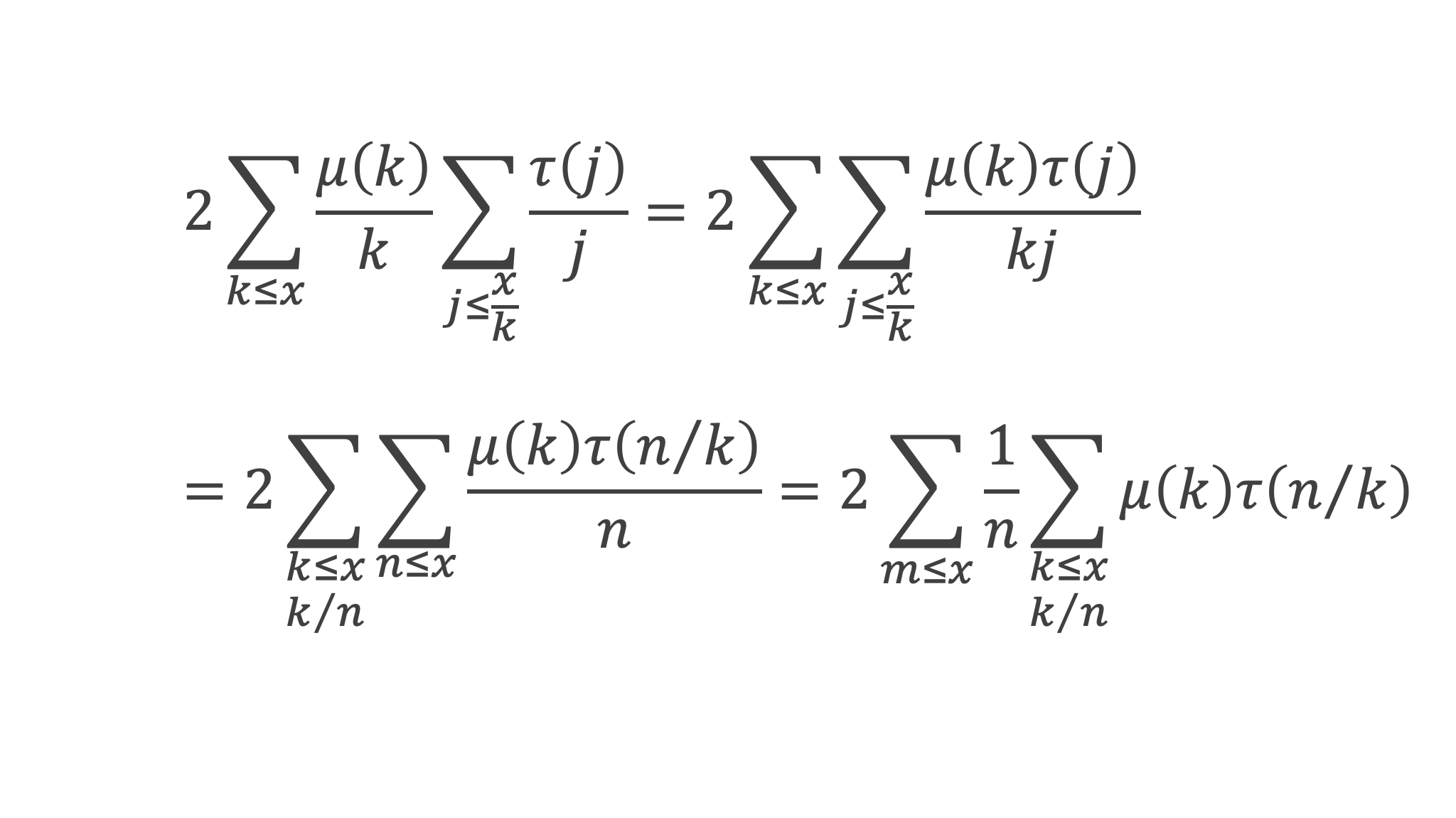
D’après le lemme 11 :

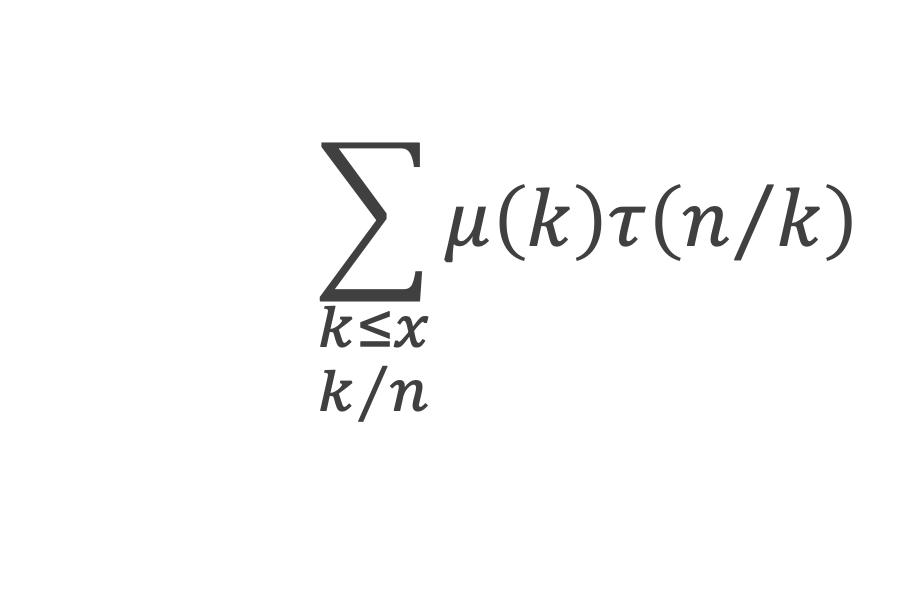
d’où, en conjonction avec le lemme 8 :

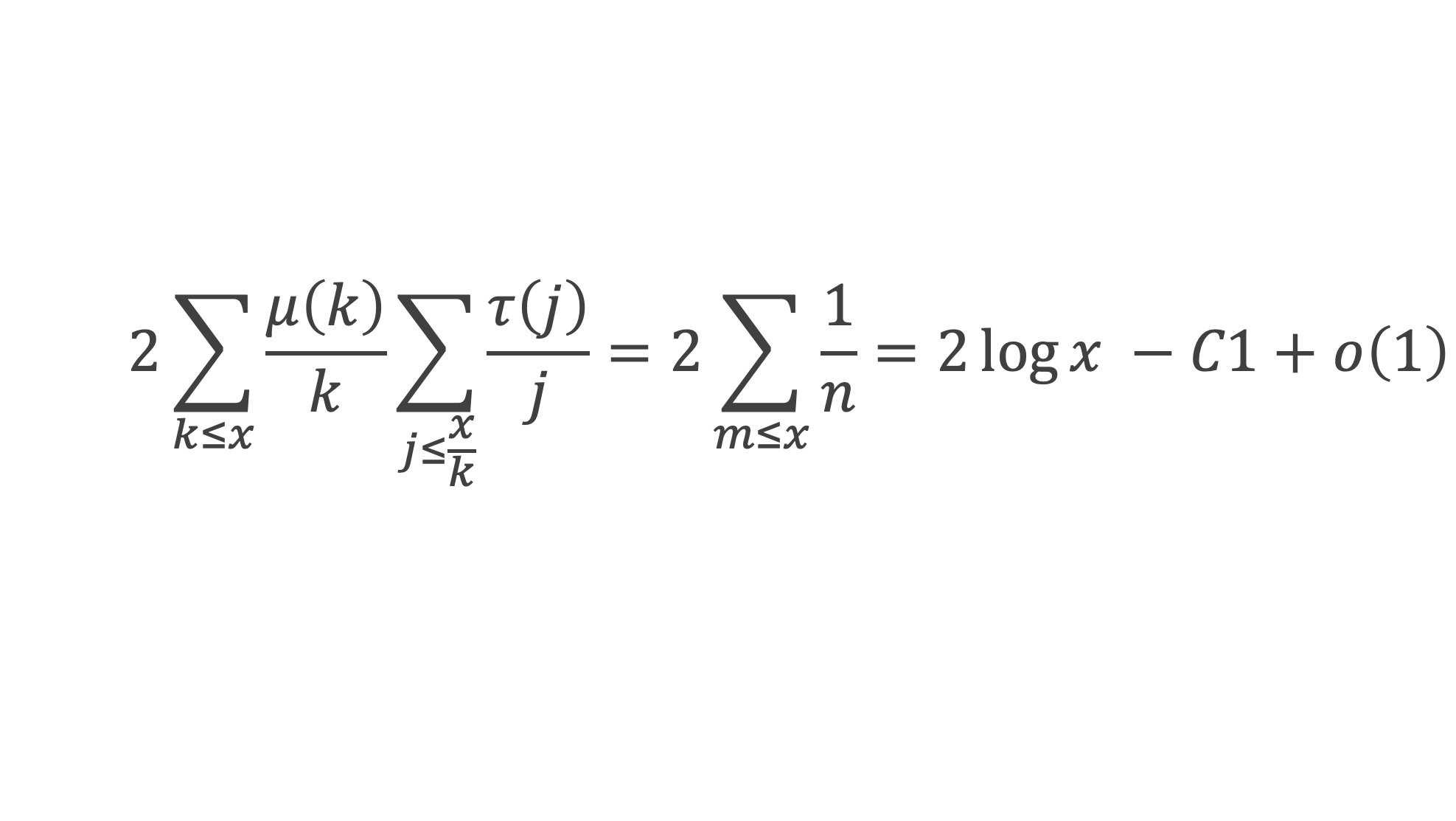
D’où finalement le lemme :

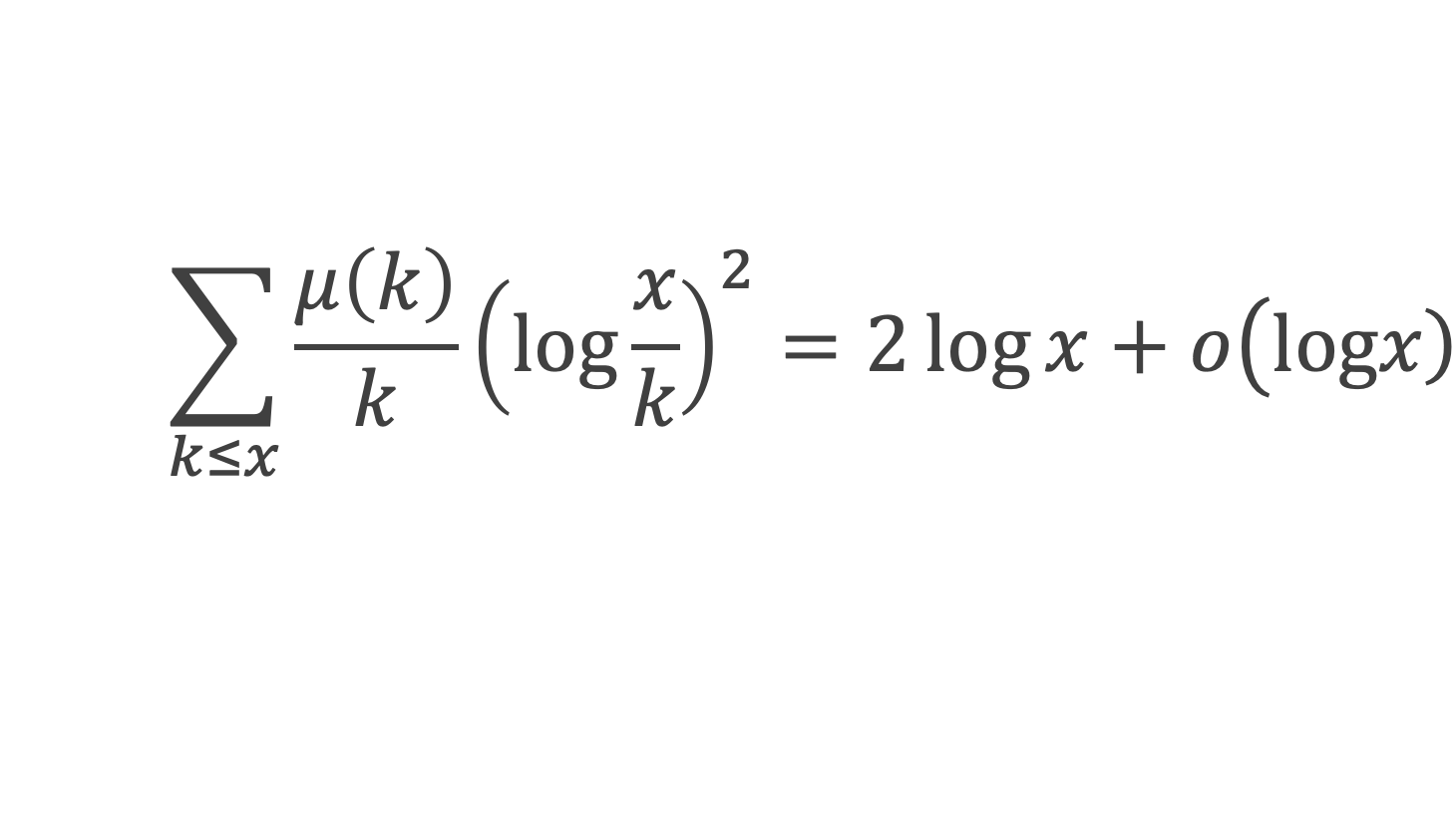
Démonstration du Théorème des nombres premiers

ETAPE 1

Il s’agit de montrer que :

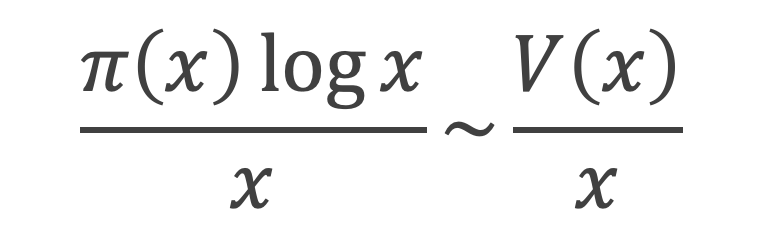
Partons de l’inégalité suivante :

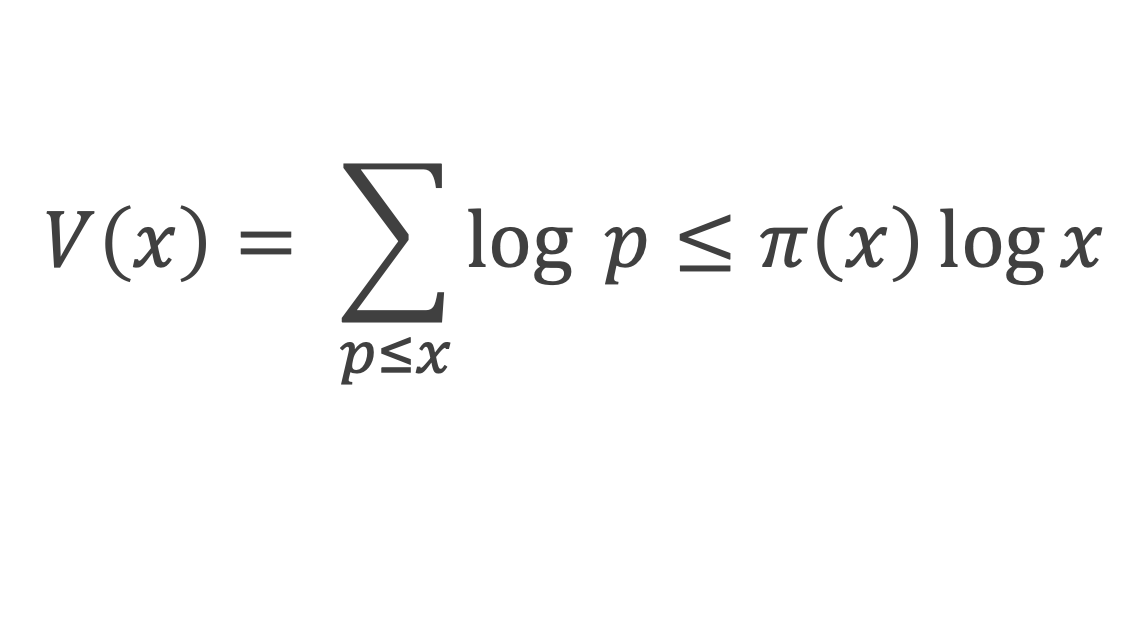
D’où : V(x)/log x ≤ π(x) et donc V(x)/x ≤ π(x) (log x)/x (I)

Par ailleurs, pour ε positif < 1 nous pouvons écrire :

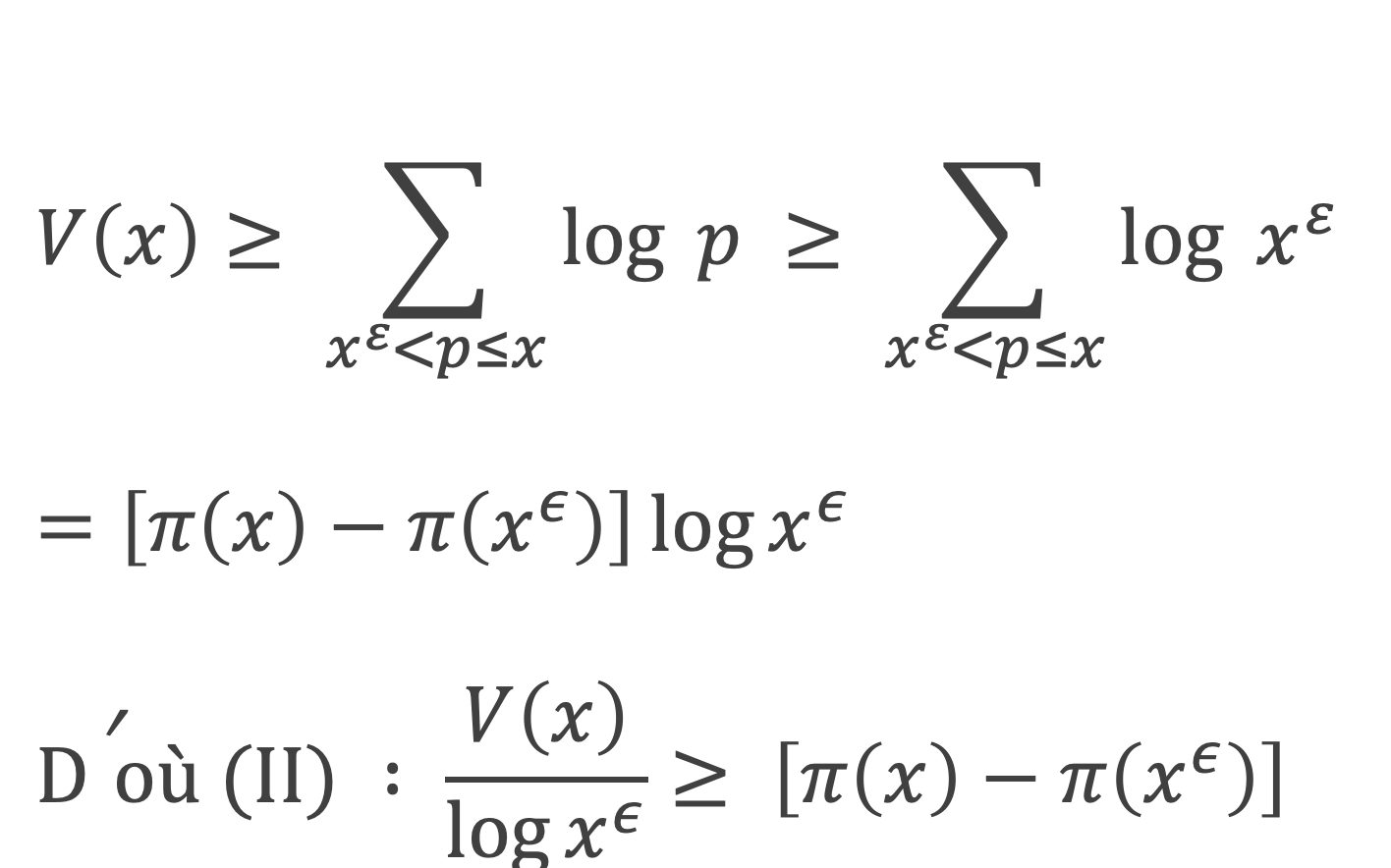
Pour tous y > 5 , π(y) < y, c’est-à-dire –y < –π(y). A partir de cette inégalité et en utilisant (II), on obtient le résultat (III) suivant : 

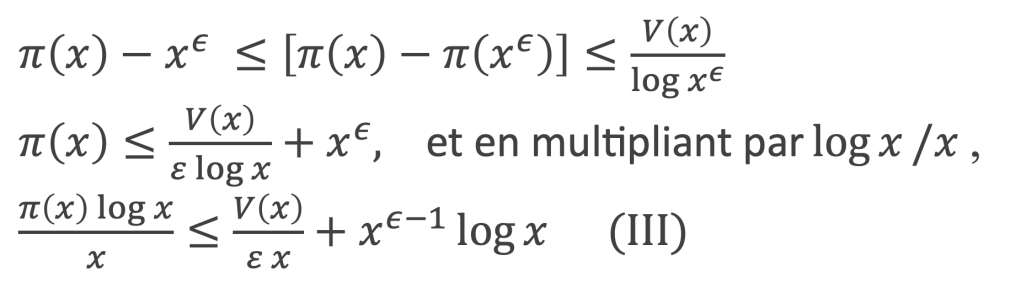
On pose ε = 1 – (log x)^-1/2 , et l’on a :

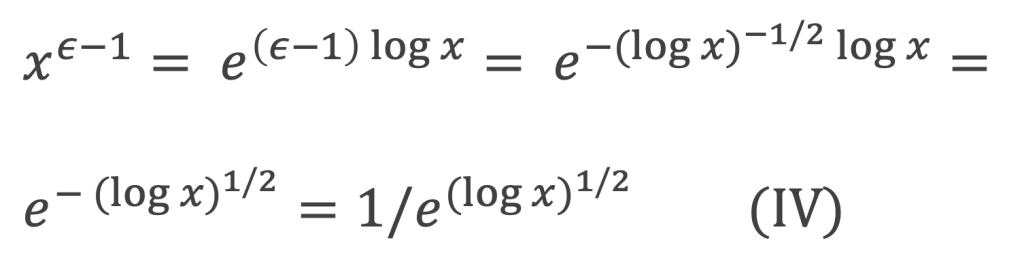
De (I), (III), et (IV) on tire :

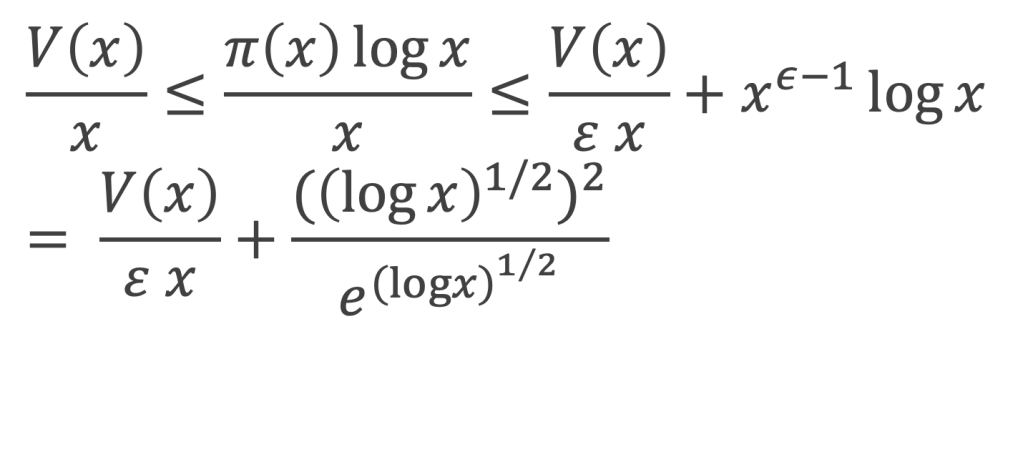
En passant à la limite lorsque x tend vers l’infini, ε tend vers 1 et (u² / e^u) tend vers 0 avec u = (log x)^1/2 qui tend vers l’infini (voir boîte à outils), donc :

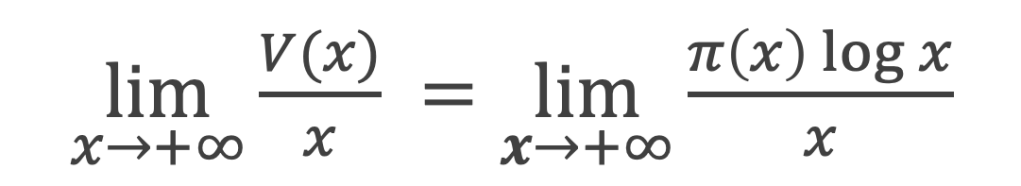
Le reste de la démonstration a pour objet de prouver que V(x) ~ x .

ETAPE 2

Montrons que V(x)/x est borné, ce sera le lemme 3 :

Lemme 3 : il existe a et A réel positifs, avec 0 < a ≤ A  tels que à partir d’un certain rang :

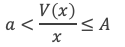
Dans un premier temps nous allons nous intéresser à la mise en évidence de la borne supérieure A.

Pour n entier > 0 on a : en se rappelant que la lettre p concerne les nombres premiers,

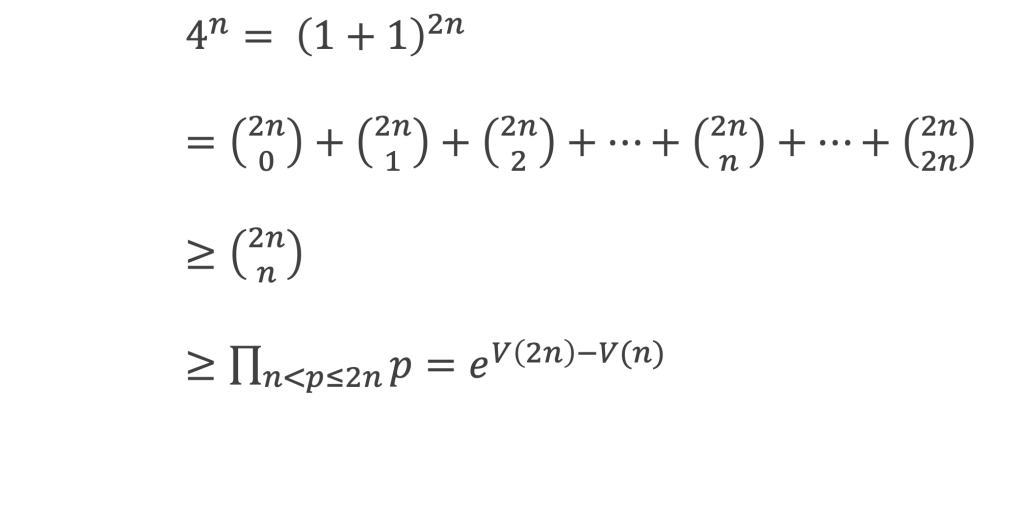
Car les nombres premiers p tels que n < p ≤ 2n au numérateur de (2n¦n)= (n+n)(n+n-1)…(n+2)(n+1)/1.2.3…n  ne peuvent être effacés par le dénominateur.

Donc, en prenant le logarithme des termes de l’inégalité (la fonction logarithme qui est croissante conserve le sens de l’inégalité), on obtiendra n log4 > V(2n) – V(n).

Appliquons maintenant cette formule sur les puissances successives de 2, on obtient :

V(2^k+1) – V(2^k) ≤ 2^k log4

V(2^k) – V(2^k-1) ≤ 2^k-1 log4

….

V(2ⁱ) – V(2^i-1) ≤ 2^i-1 log4

V(2^i-1) – V(2^i-2) ≤ ^i-2 log4

…

V(2²) – V(2¹) ≤ 2¹ log4

V(2¹) – V(2⁰) ≤ 2⁰ log4

Et en faisant la somme de toutes ces inégalité, cela donne : V(2^k+1) – V(1) < 2^k+1 log4, sachant que V(1) = 0 et que somme des 2ⁱ pour i = 0 à i = k est 2^k+1.

Comme pour tout x rée > 1 il existe k_x tel que 2^k_x ≤ x < 2^k_x+1 , il vient par croissance de V(x):

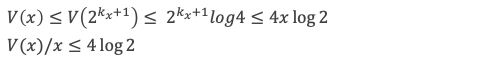
Montrons maintenant qu’il existe aussi une constante a > 0 telle que V(x) ≥ a_*x .

Pour tout nombre premier p de la série des nombres entiers 1, 2, 3, …, n, cette série contient exactement [n/p] multiples du nombre premier p, [n/p²] multiples de p², [n/p³] multiples de p³, etc…, de sorte que si l’on considère le produit de tous les termes de 1 à n, c’est à dire n!, ce produit s’exprime sous la forme:

n! = p^[n/p] p^{[n/p^2]} p^{[n/p^3]} … p^{[n/p^k]}_*J avec J nombre entier ne comprenant plus le nombre premier p.

Clarification de ce résultat : la contribution de chaque nombre multiple de p² dans ce produit sera bien de p puissance 1 déjà compté à travers [n/p] puis p puissance 1 compté à travers [n/p²] ce qui donnera bien p² au total lorsque l’on forme le produit. De même la contribution de chaque nombre multiple de p³ dans ce produit sera bien de p¹ à travers [n/p] puis p¹ à travers [n/p²] puis p¹ à travers [n/p³] soit p³ au total, etc…

Le raisonnement précédent étant valable pour tous les nombres premiers de 1 à n, on peut donc finalement écrire : 

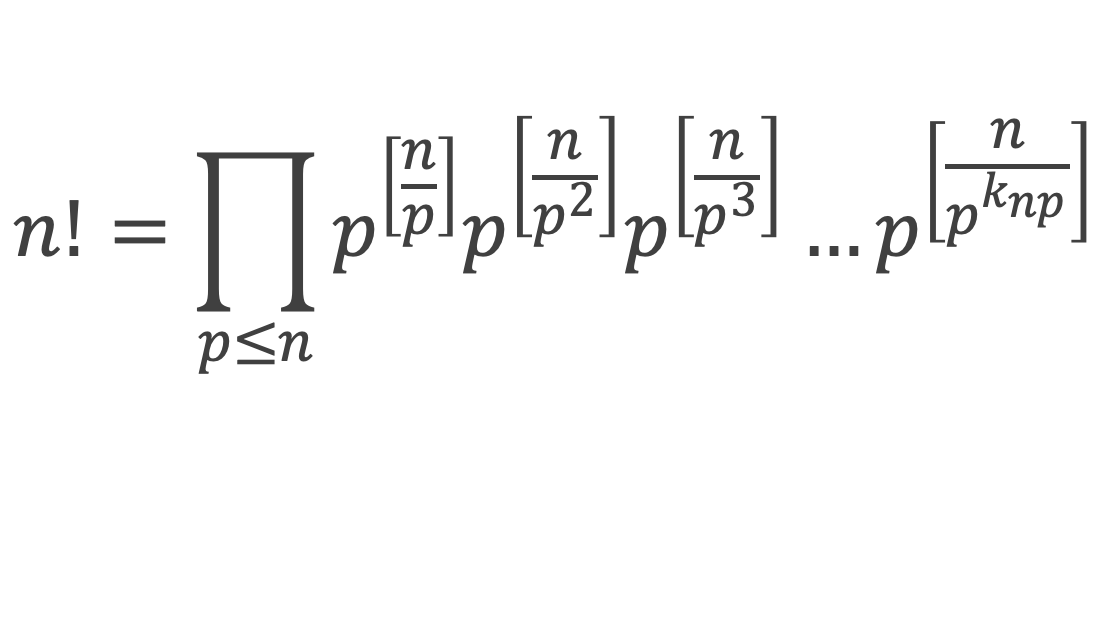
Où k_np est la plus grande puissance de p telle que [n/p^k_np] ≥ 1, (les puissances supérieures donneront 0).

Repartons de (2n¦n) qui est la notation pour (2n)!/(n!_*n!) et notons k_2np la plus grande puissance de p telle que [2n/p^k_2np],

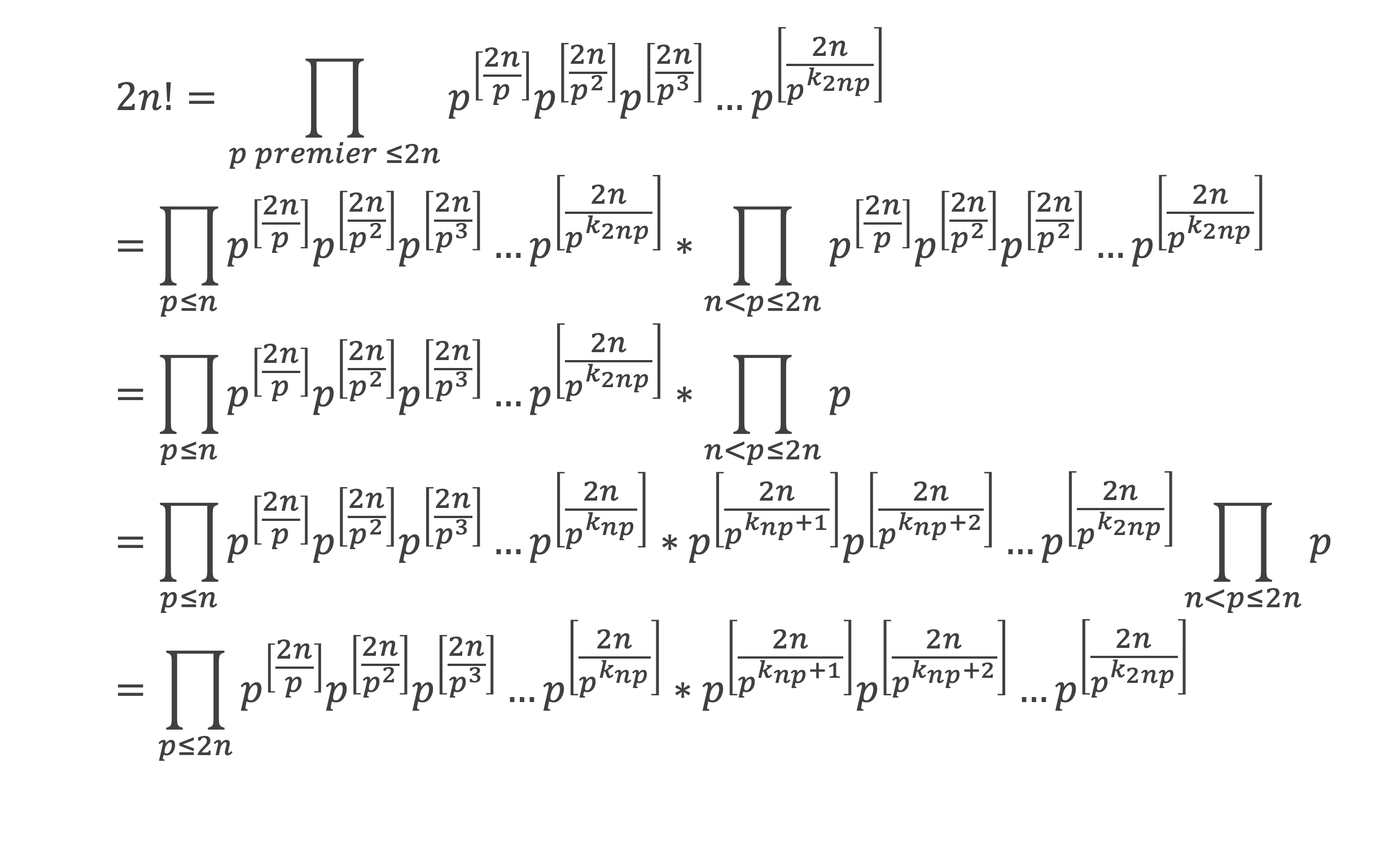
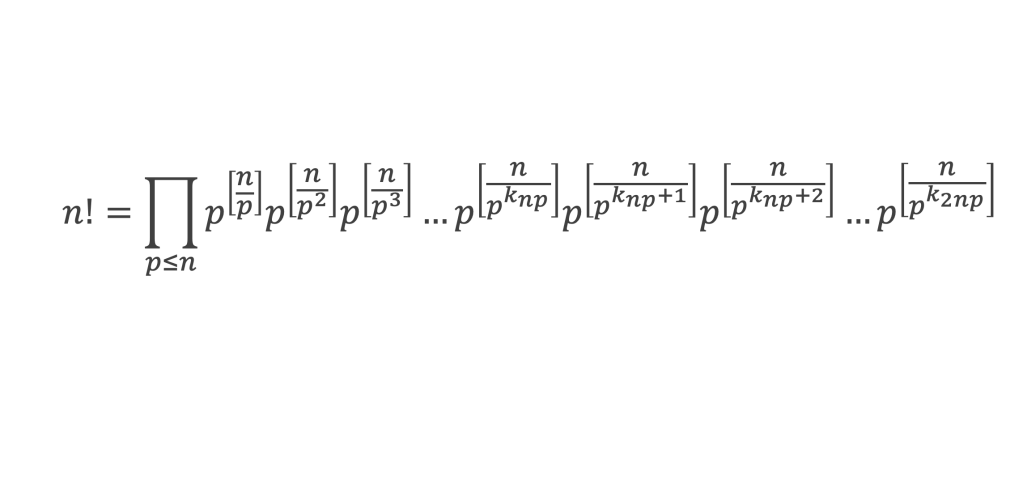
On en déduit l’expression Q_p de l’exposant de chaque nombre premier p compris entre 1 et n, dans (2n)!/(n!_*n!).

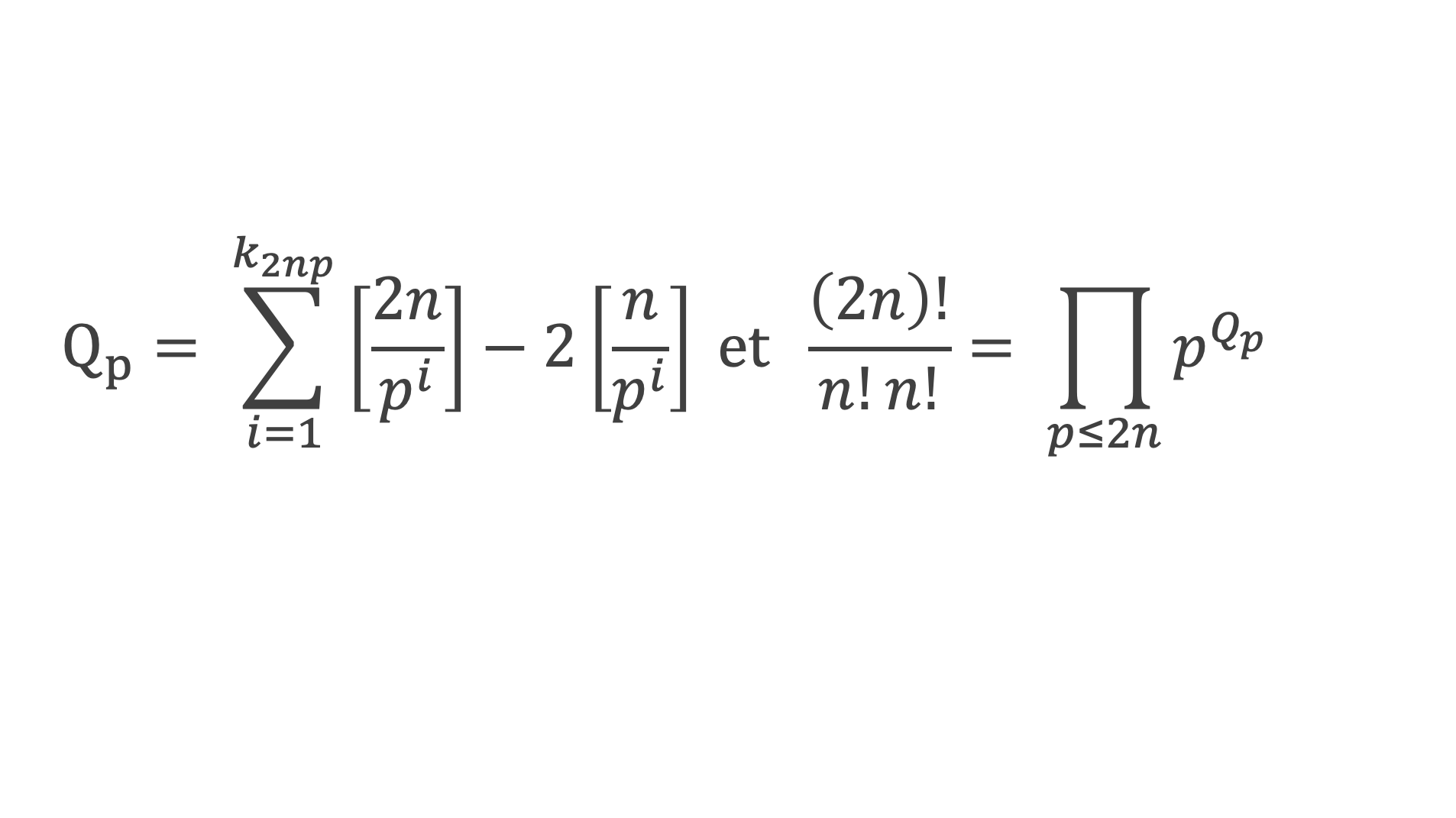
C’est-à-dire, sachant que [2n/p^k_2np] ≥ 1 implique log 2n > k_2np log p, c’est à dire k_2np < log 2n/log p ou encore k_2np ≤ [log 2n/log p] : Q_p ≤ k_2np ≤ [log 2n/log p].

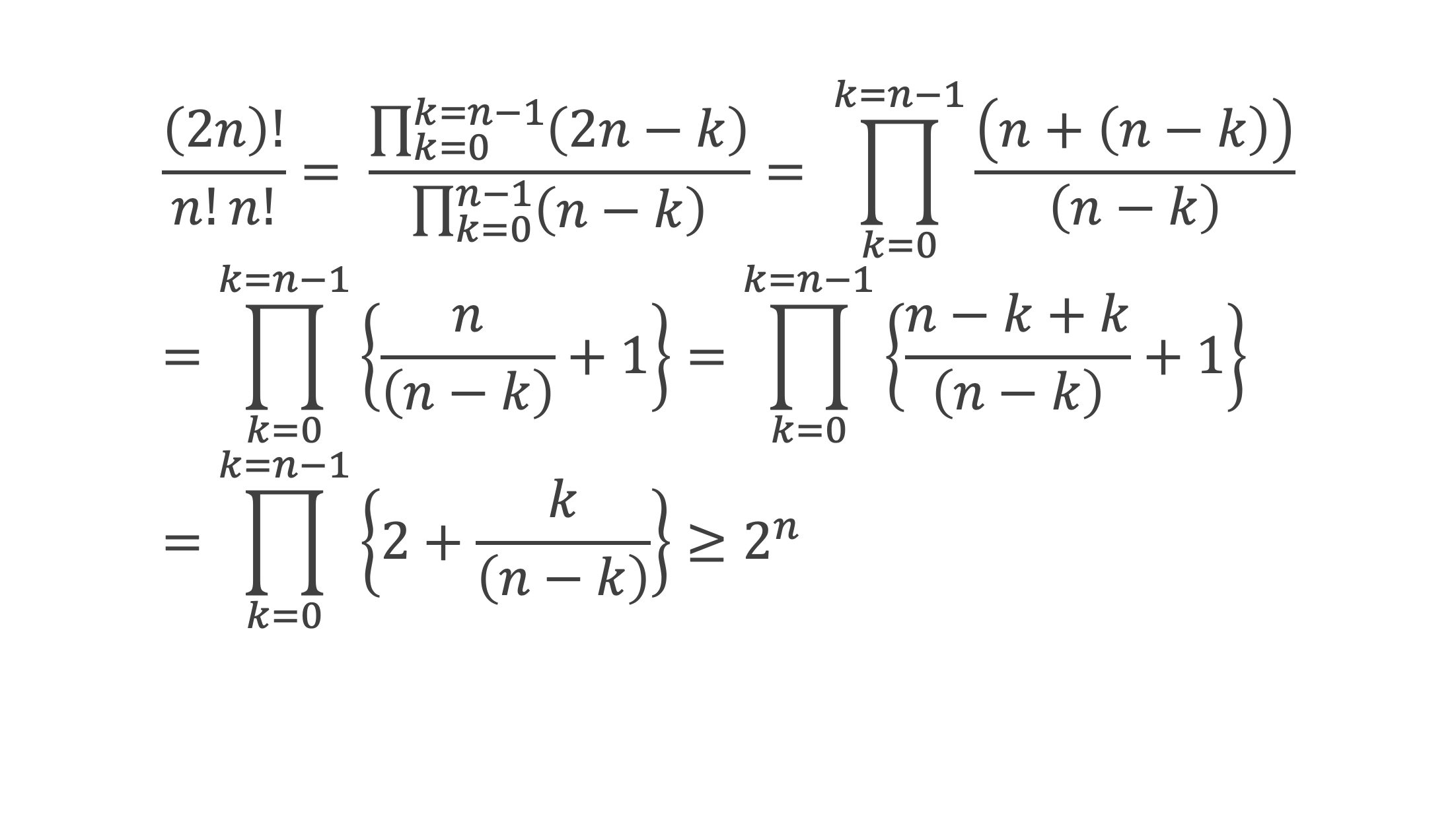
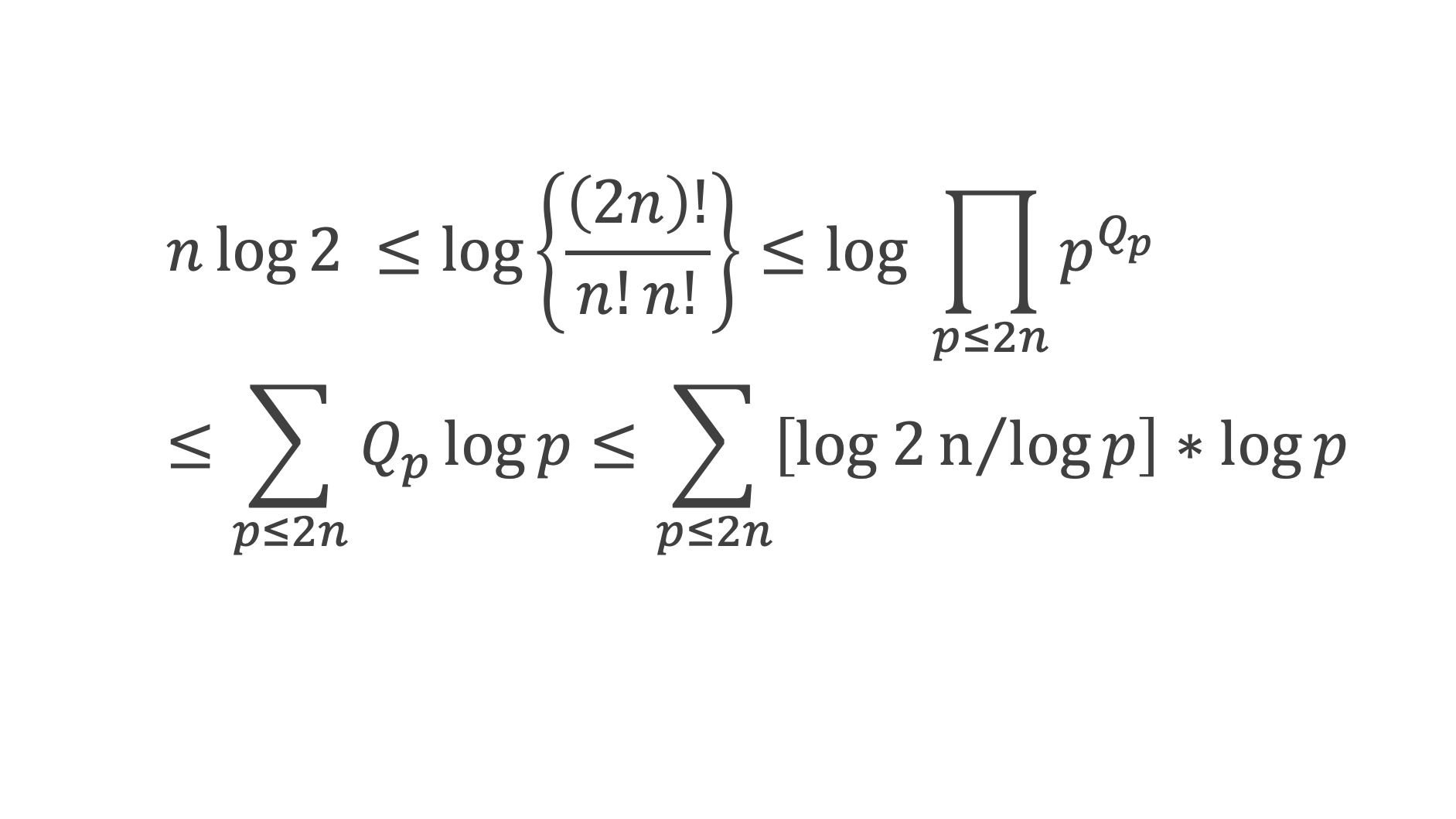
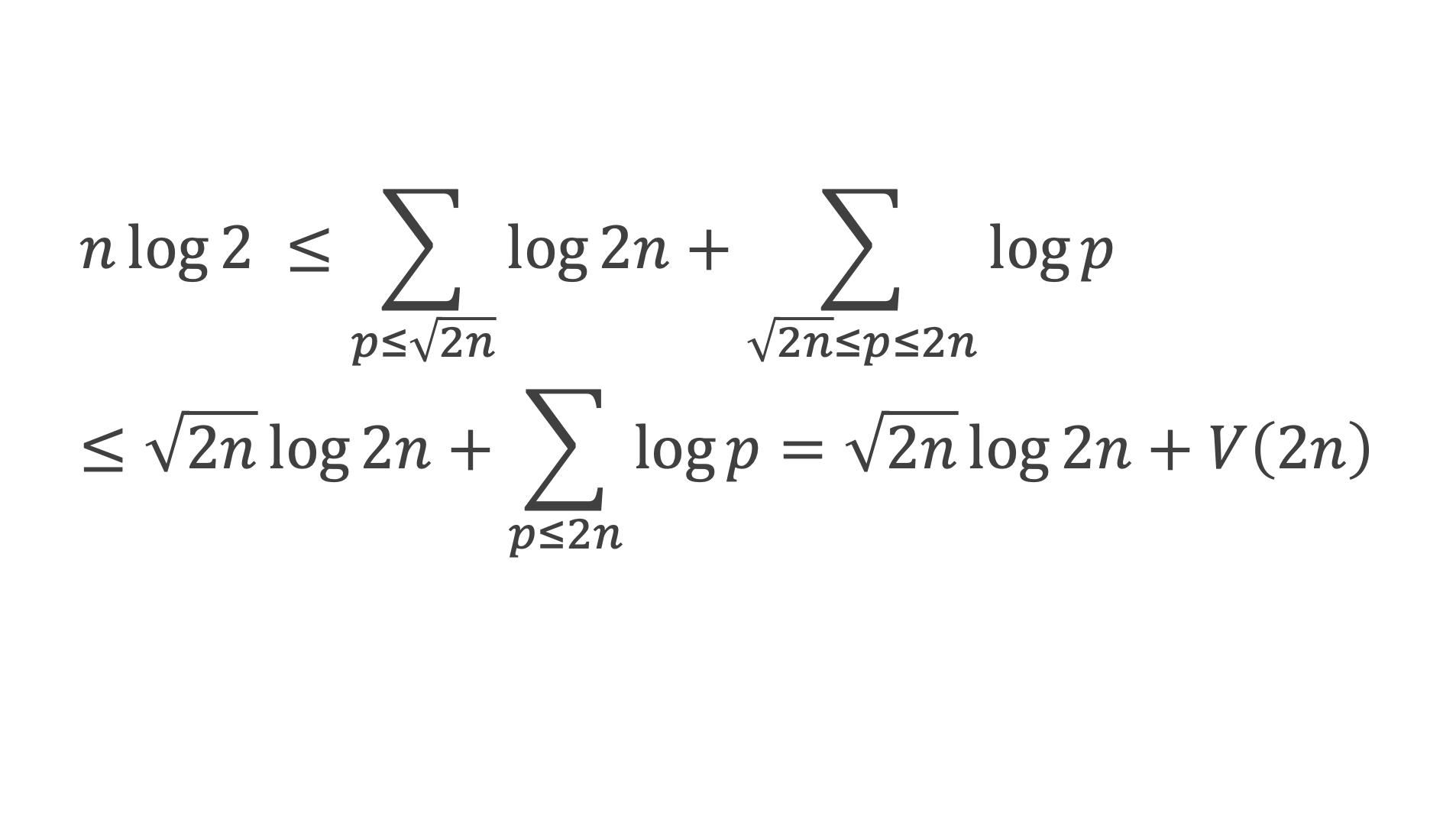
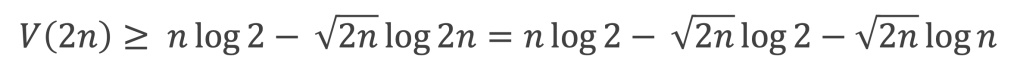
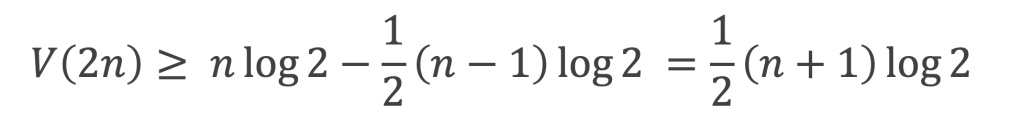
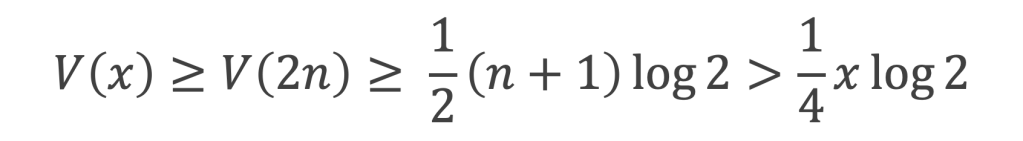
Conclusion : il existe bien a et A réel positifs, avec 0 < a ≤ A tels qu’à partir d’un certain rang :

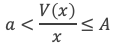
On a d’ailleurs démontré que : a > (log 2)/4 et A ≤ 4 log 2 .

ETAPE 3

Nous voilà arrivés à l’étape 3 dont l’objet est de démontrer que a + A = 2. Pour cela nous avons besoin de disposer de la formule de Selberg, et pour disposer de cette formule nous devons auparavant démontrer les 3 lemmes qui suivent . Il s’agit des lemmes 4, 5 et 6.

Lemme 4 : Pour p premier,

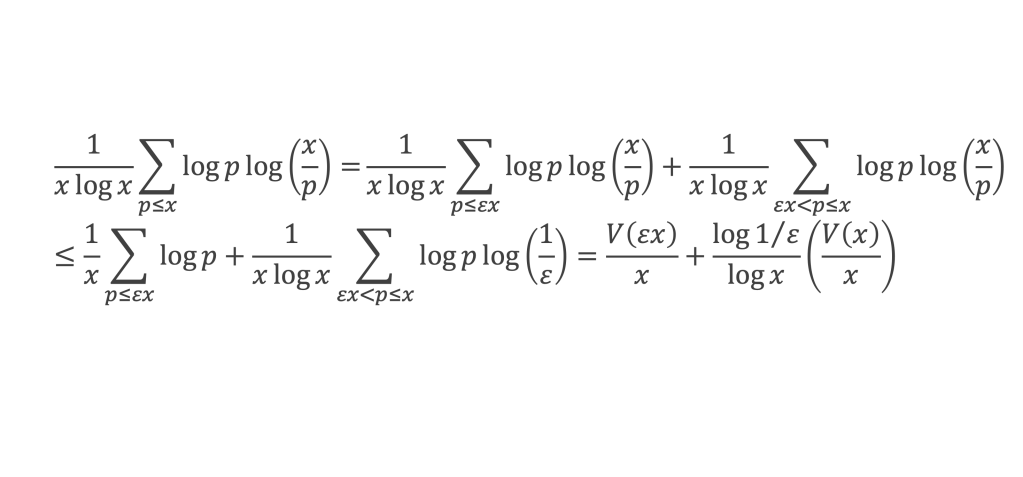
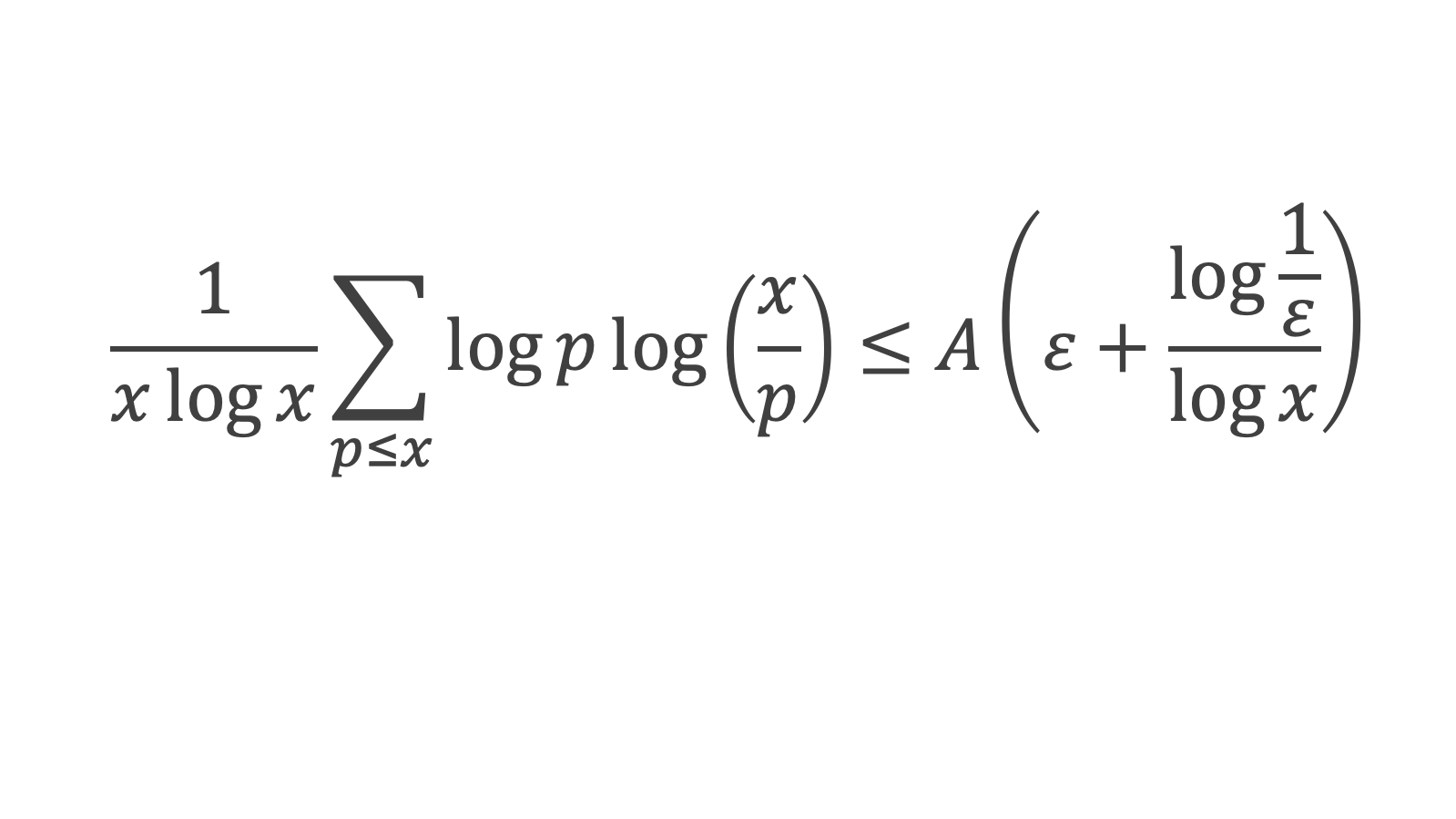
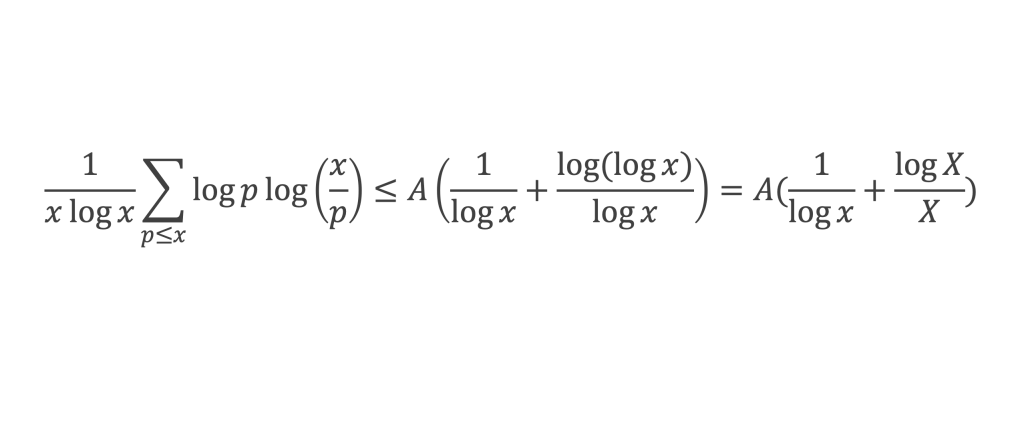
lim (log X )/ X = 0 quand x tend vers +∞, car alors X = log x tend vers +∞. Comme également lim (1/log x ) = 0 quand x tend vers +∞, le lemme 4 est démontré.

Lemme 5 : Pour α entier et p premier,

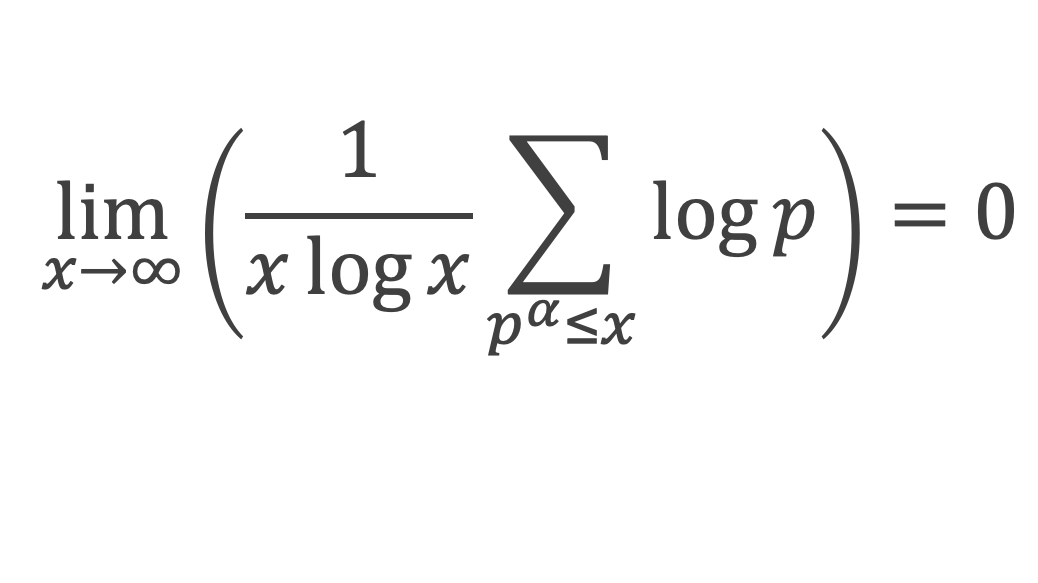
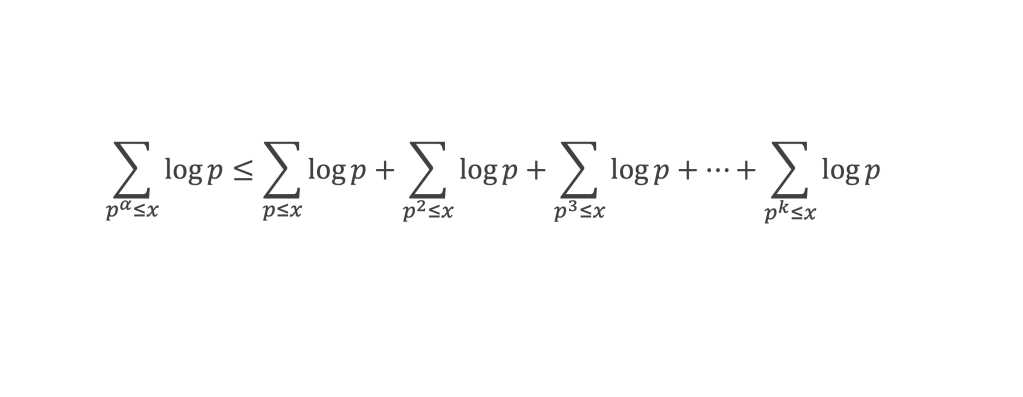
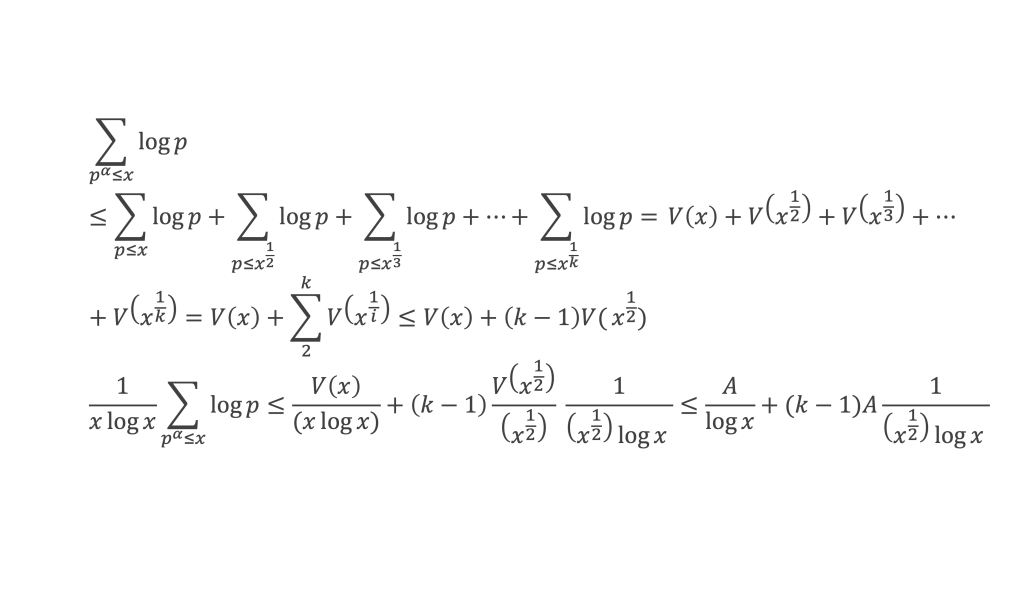
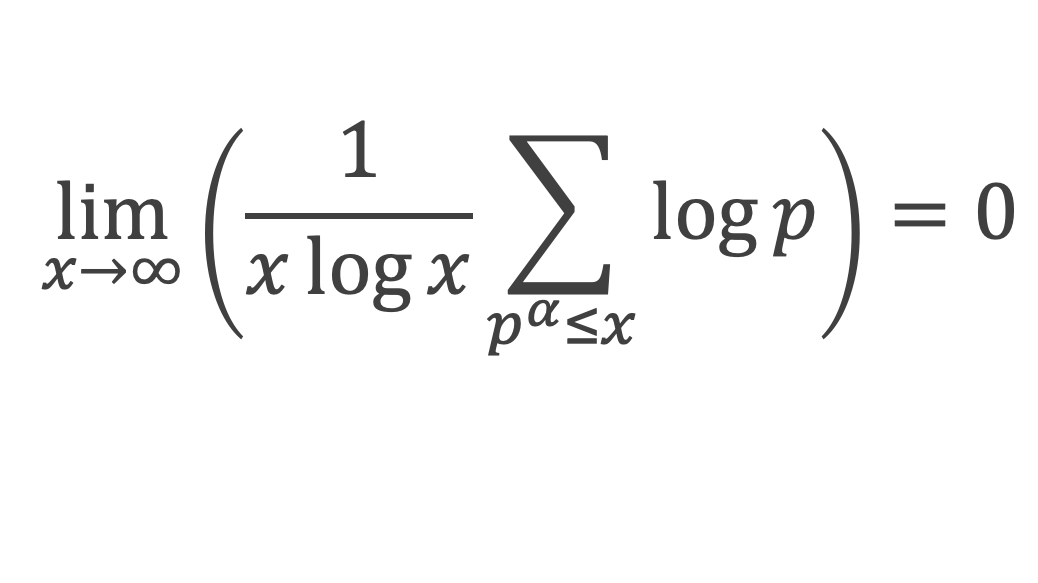
Lemme 6 : La fonction f(m) introduite au lemme 2 (cf boîte à outils) vérifie :

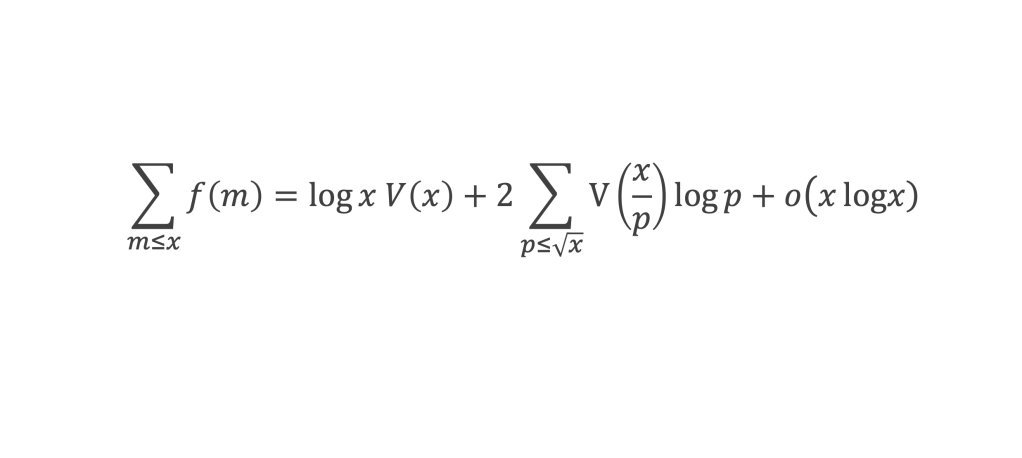
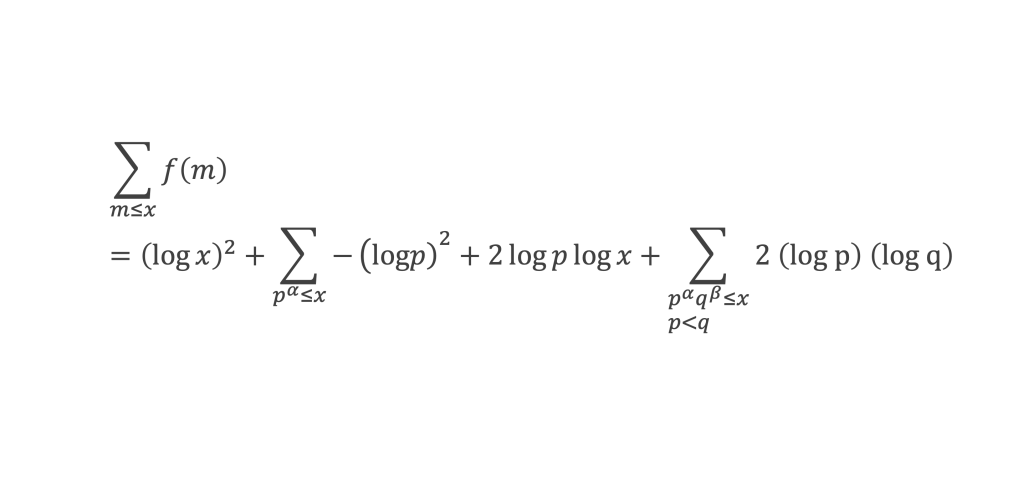
• Evaluation du premier terme : (log x)² est un o(x log x ) : en effet (log x)²/(x log x) = log x /x qui tend vers 0 quand x tend vers +∞.
• Evaluation du deuxième terme : considérons la somme des – (log p)² + 2 log p log x qui est établi sur les p^α ≤ x, et étudions de façon séparée les cas α ≥ 2 et α < 2.

Cas α ≥ 2 :

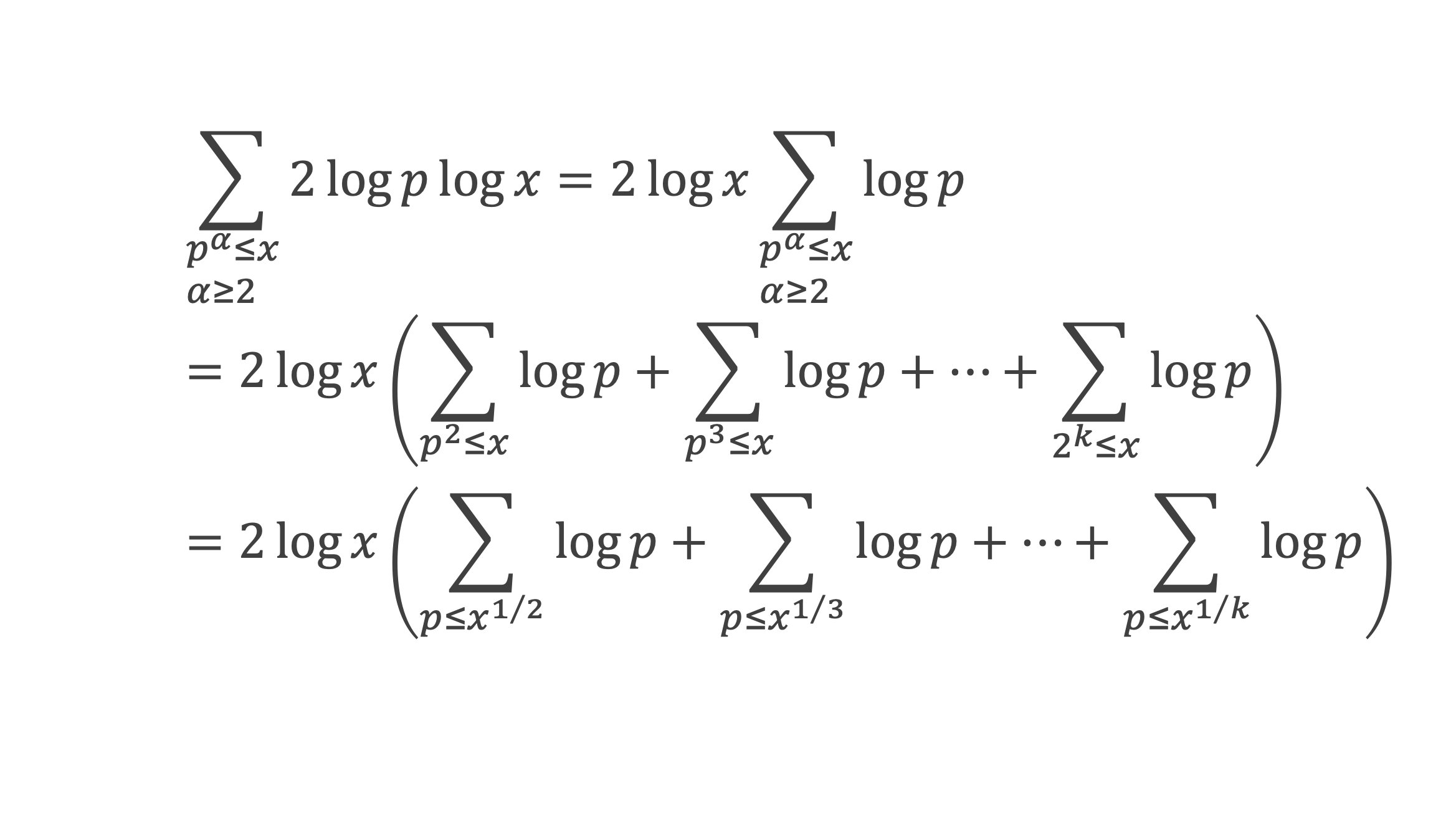
Maintenant en remplaçant p par la valeur maximale x^1/i dans chacune des sous sommes cela donne l’inégalité suivante :

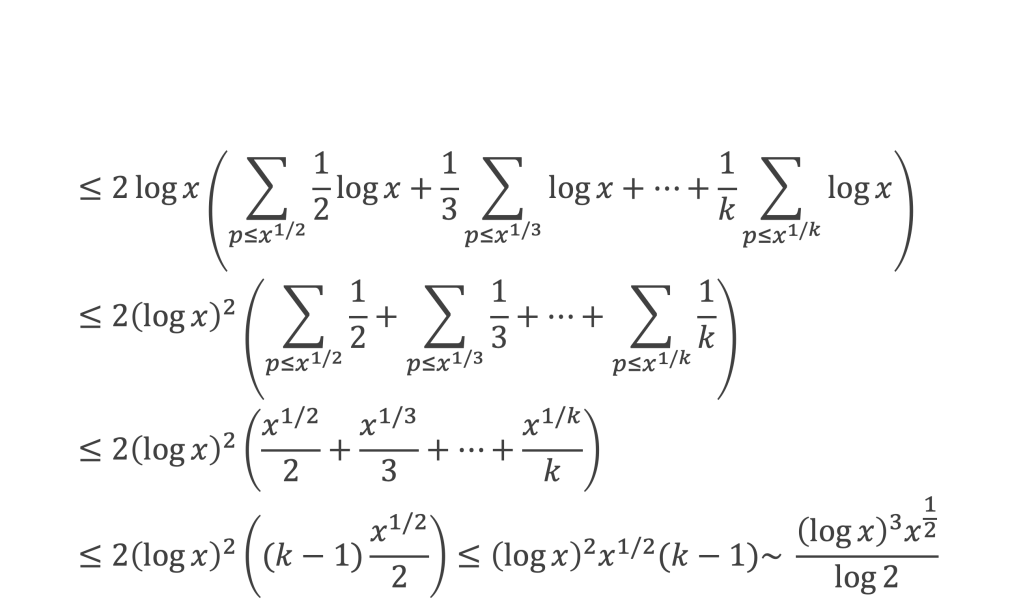
Donc lorsque α ≥ 2 la somme sur les 2 log p log x est bornée par : (log x)³x^1/2 / log 2 qui est un o(x log x). De même la somme sur les (log p)² sera inférieure à la somme sur les log p log x que l’on vient de calculer, ce sera donc un o(x log x). Conclusion: la somme des – (log p)² + 2 log p log x établie sur les p^α ≤ x avec α ≥ 2 est un o (x log x).

Cas α < 2 : Pour α < 2 , c’est-à-dire α = 1, la somme s’écrit :

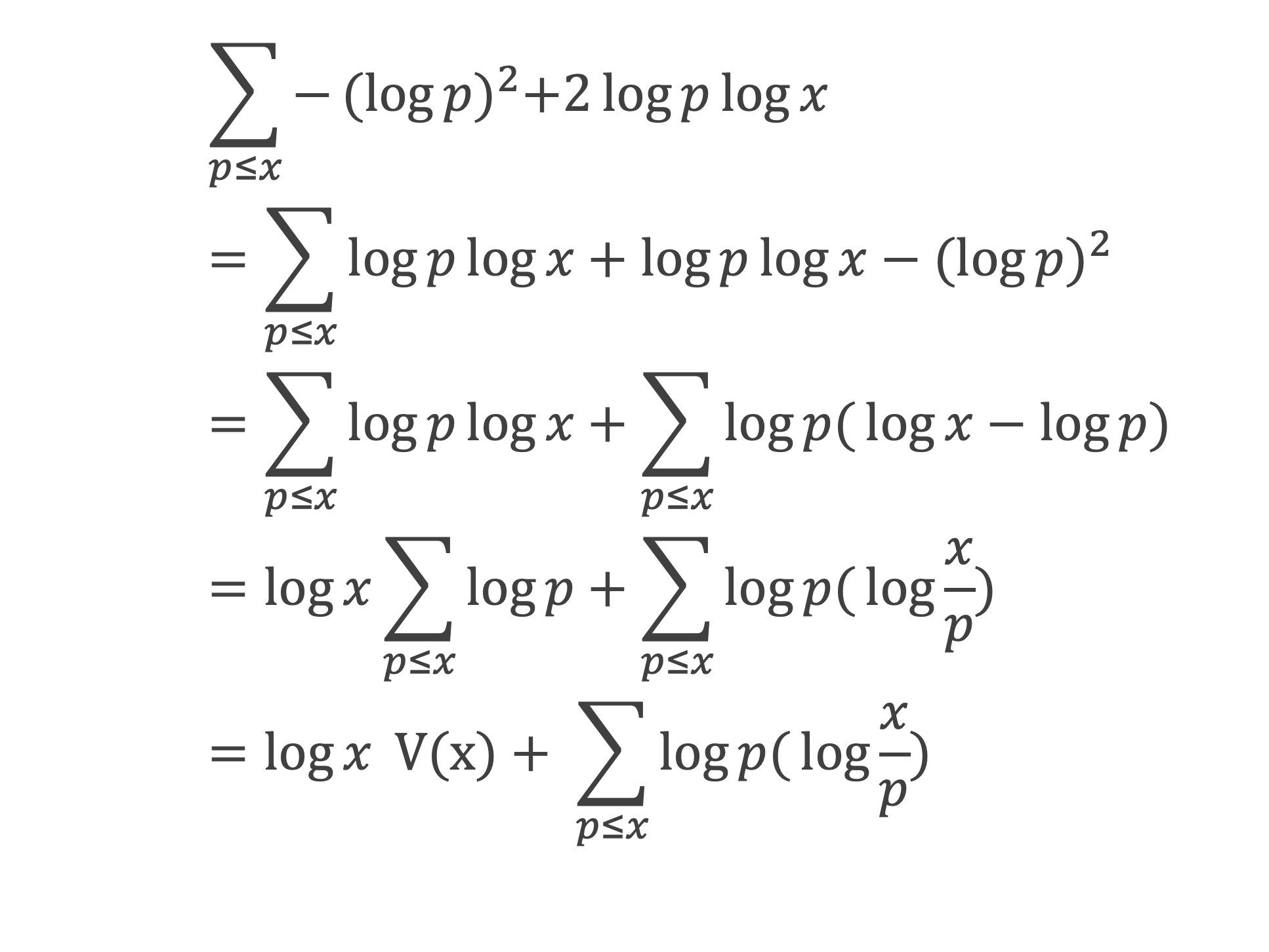
Les cas α ≥ 2 et α < 2 permettent de conclure que :

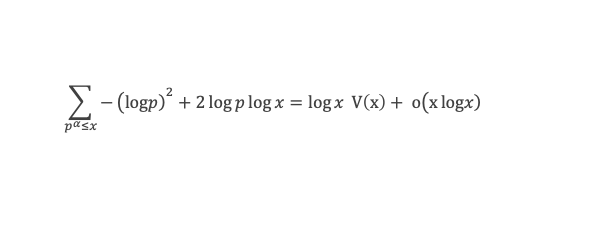
• Evaluation du troisième terme: le terme en question s’écrit ∑_p^αq^β≤x 2(log p)(log q). Nous allons successivement regarder la contribution des cas β ≥ 2 et α ≥ 1, α ≥ 2 et β ≥ 1, puis du cas β = α = 1

Cas β ≥ 2 et α ≥ 1

Appliquons le lemme 5, avec x/q^βau lieu de x : 

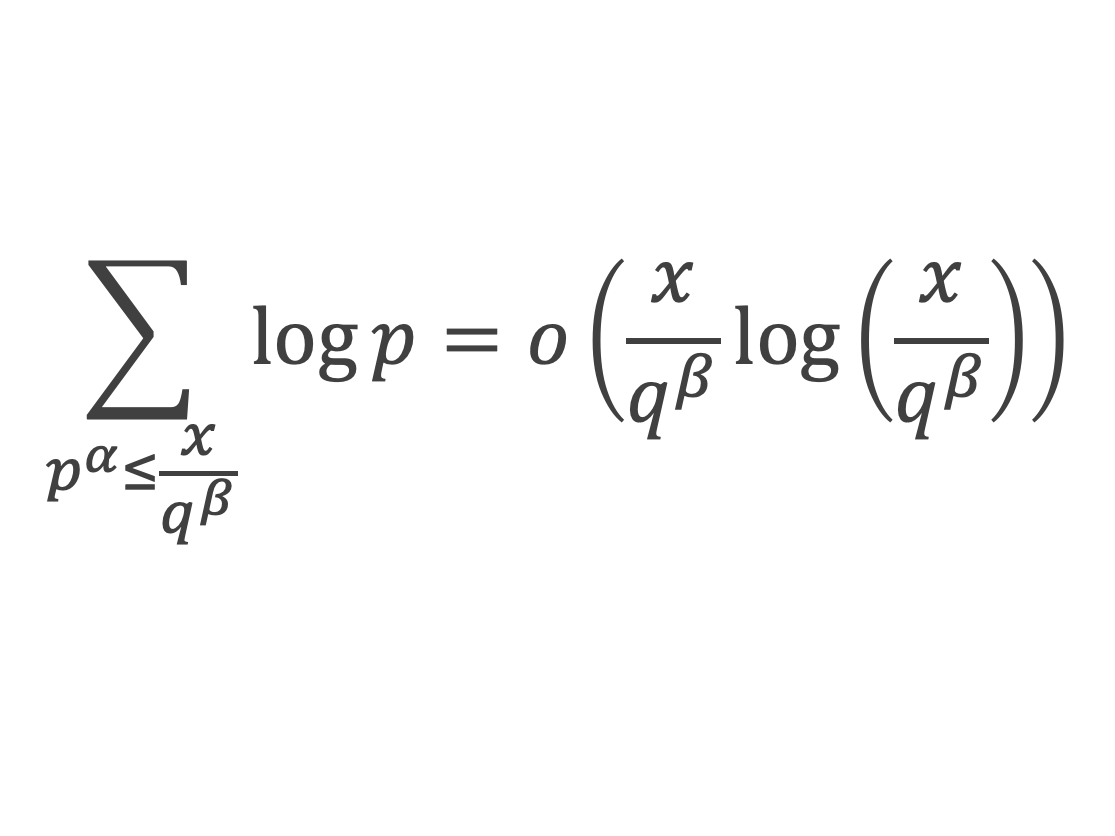
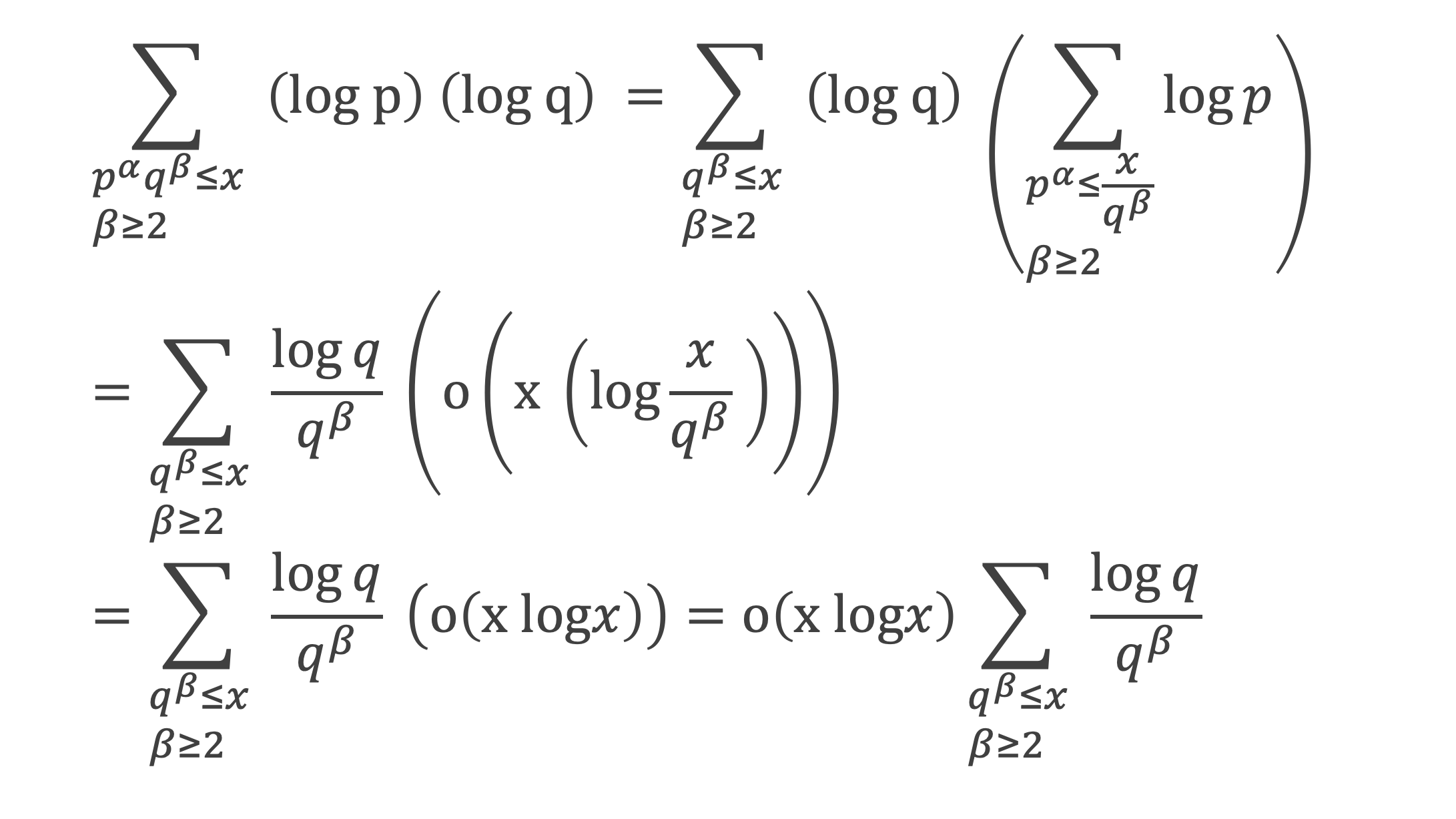
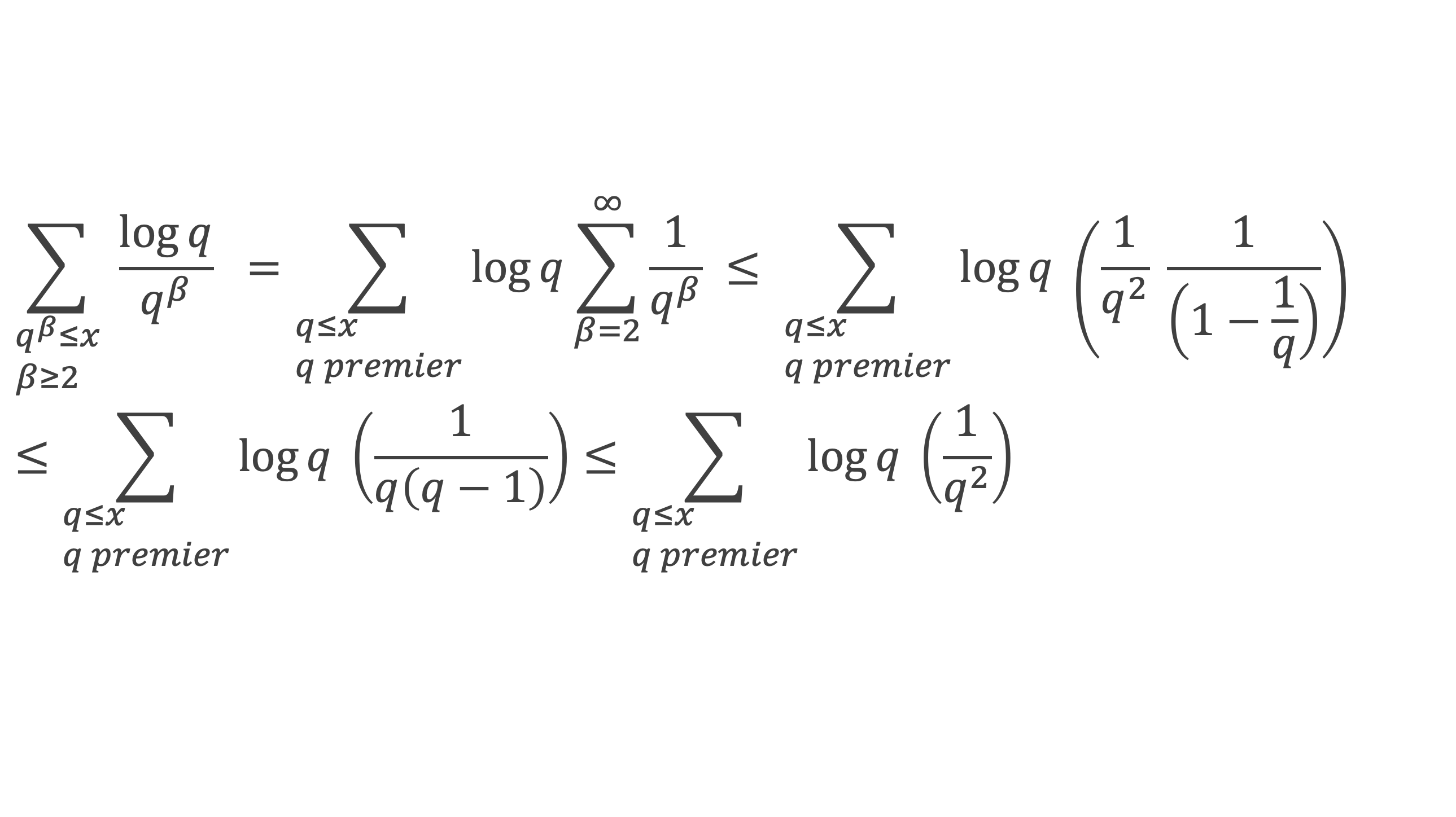
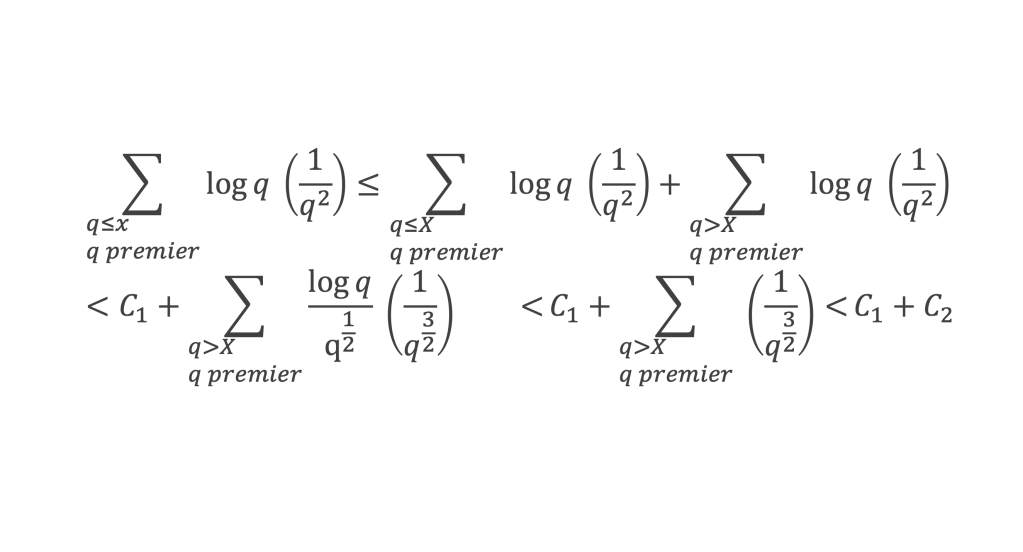
Cela permet de conclure que pour ce qui est de la contribution des termes β ≥ 2 et α ≥ 1 :

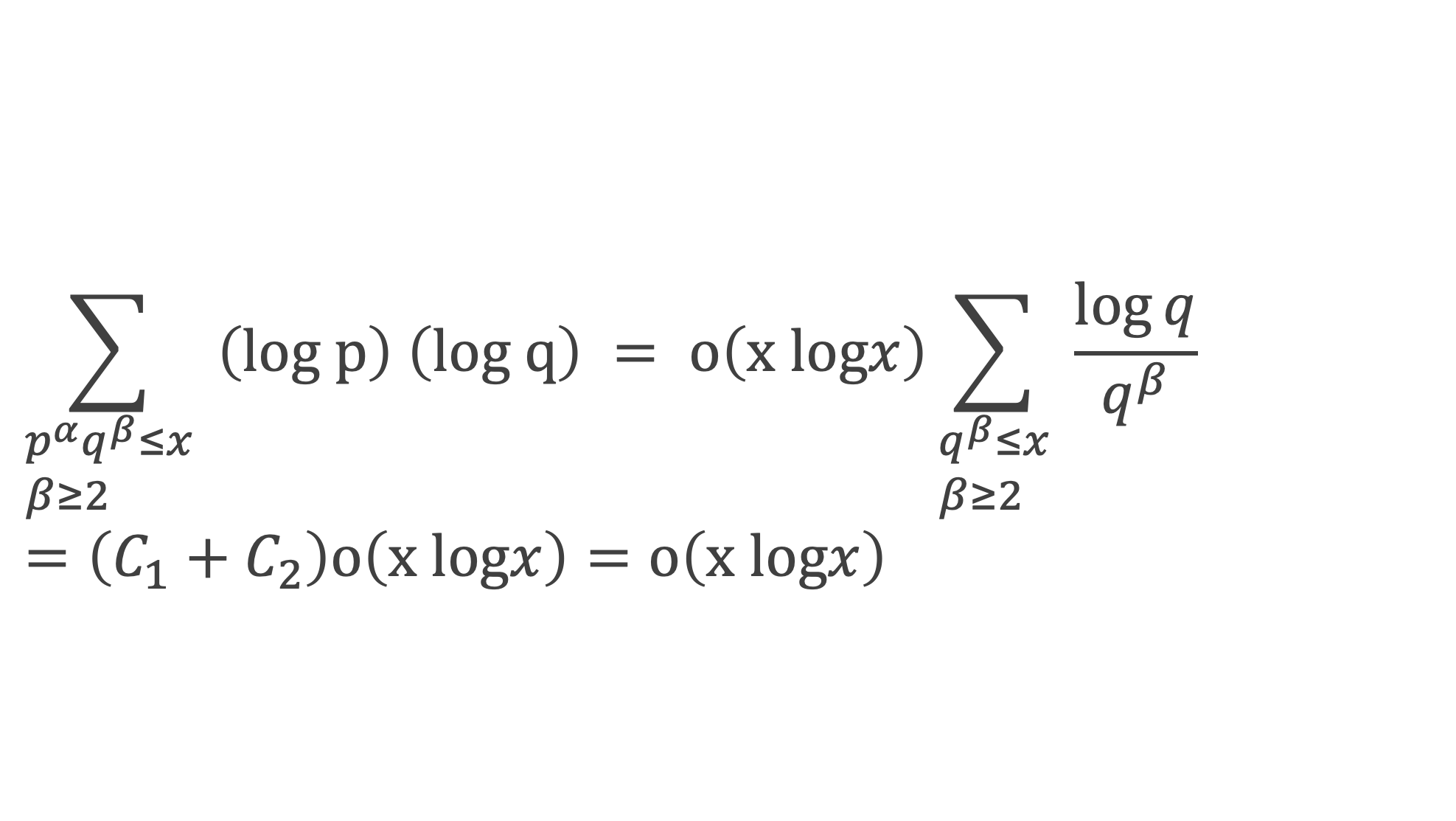
Cas α ≥ 2 et β ≥ 1 : p et q, et α et β ayant des rôles symétriques, la contribution des termes α ≥ 2 et β ≥ 1 sera elle aussi un o(xlog x).

Cas α = 1 et β = 1 :

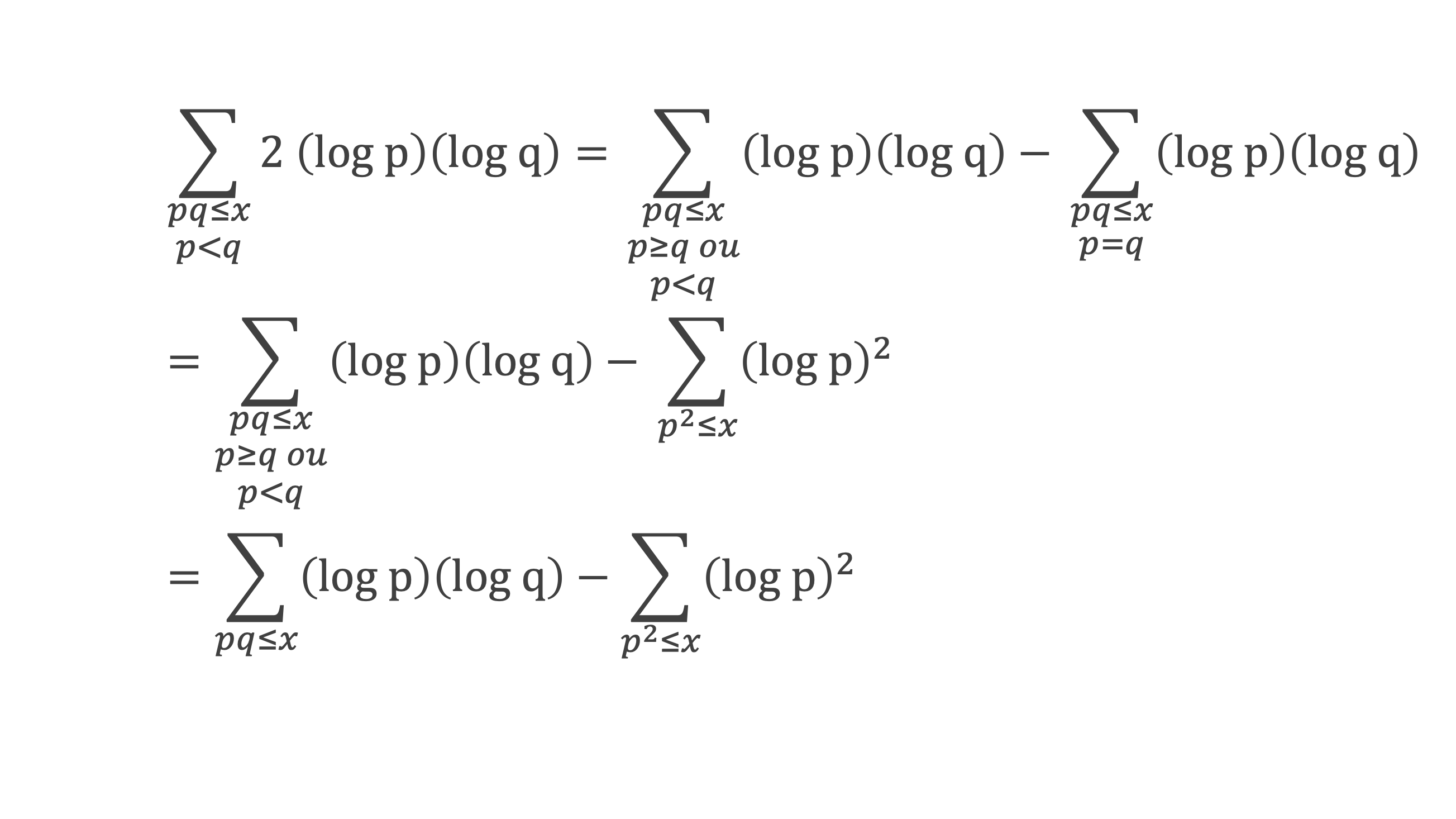
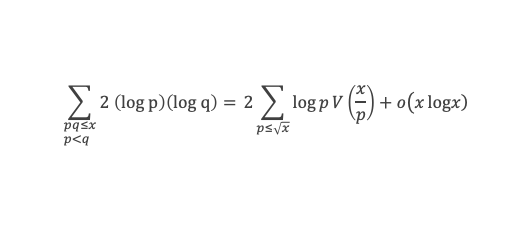
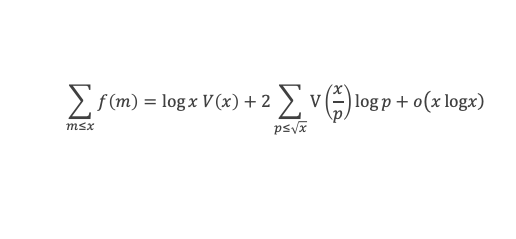
Grâce aux lemmes 3, 4, 5, 6, et des lemmes de la boîte à outils, nous voilà armés pour démontrer la formule de Selberg, à savoir :

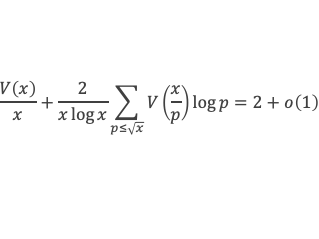
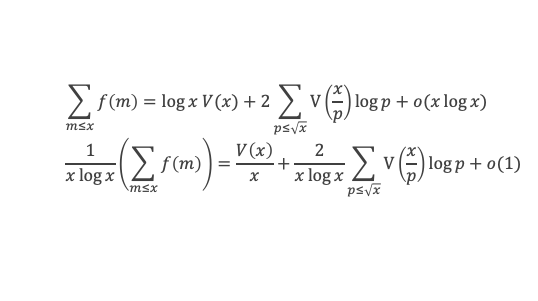
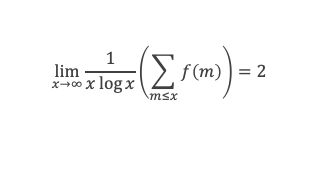
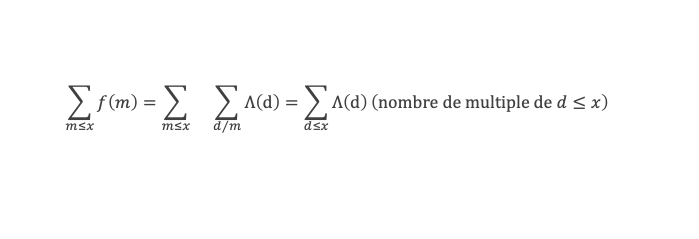
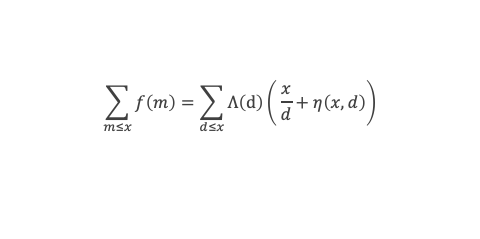
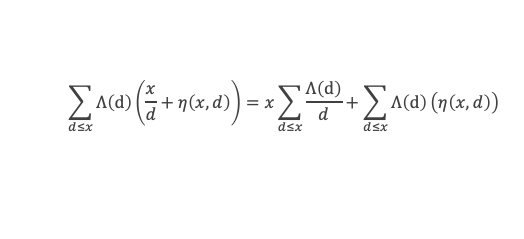
En remplaçant Λ(d) par sa définition, puis en utilisant le lemme 12 de la boîte à outils, cela donne :

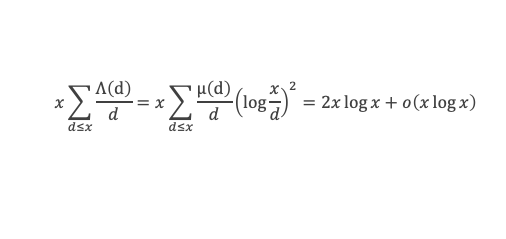
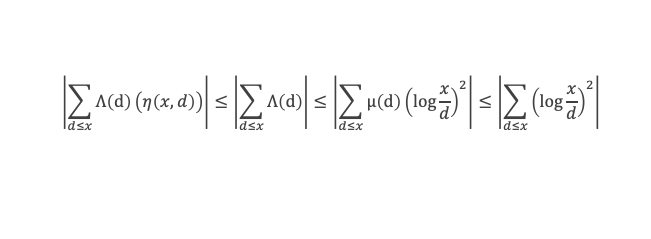
La valeur des x/d varie de 1 à x. Découpons l’intervalle 1 … x par tranches de puissances de 2. Pour tous les d tels que x/d est dans la tranche 2^k+1 > x/d ≥ 2^k on a :

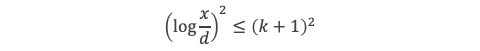
et comme d ≤ x/2^k , il y a au plus x/2^k contributeurs dans cette tranche. Donc la contribution des valeurs de la tranche 2^k – 2^k+1 est au plus  x (k + 1)²/2^k, et la contribution totale de toutes les tranches sera :

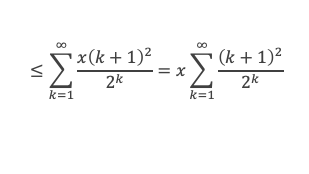
Or à partir d’un certain rang on a (k+1)² < 2^k/2 en vertu de log(k+1) / k < log(2) / 4 à partir d’un certain rang puisque log(k+1) / k tend vers 0 quand k tend vers l’infini. On aura donc :

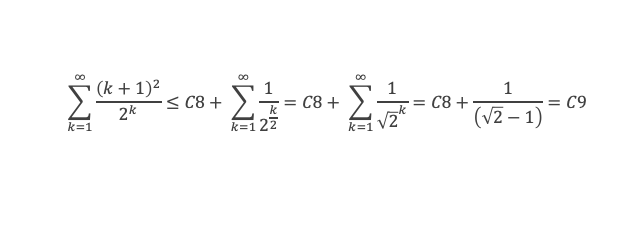
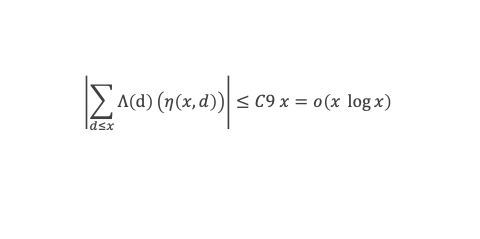
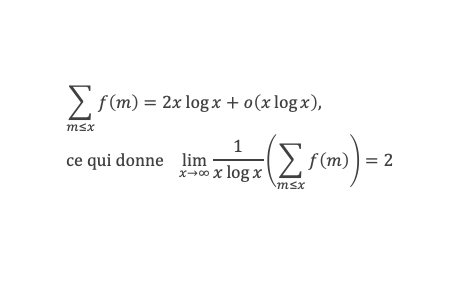
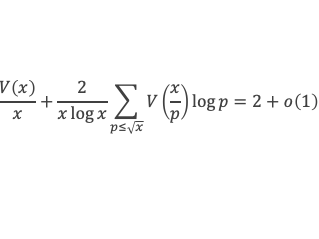
La formule de Selberg est démontrée, nous pouvons passer à la suite de la démonstration et terminer l’étape 3 en montrant que : a + A = 2.

Et pour cela commençons par démontrer le lemme 13 :

Lemme 13 :

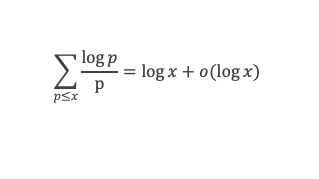
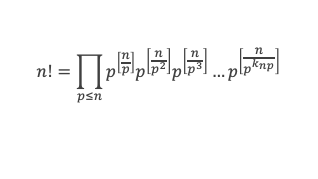
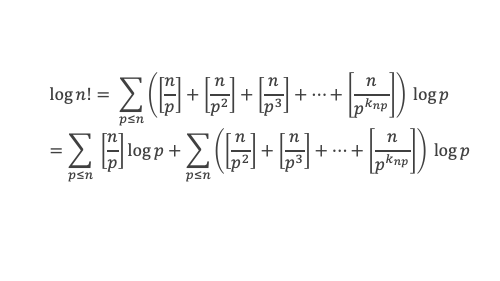
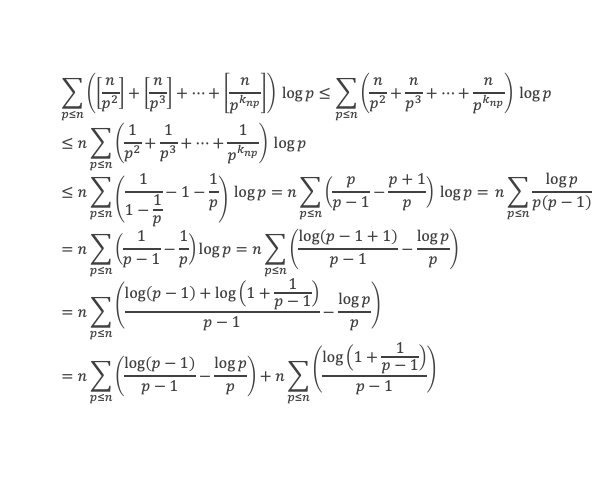
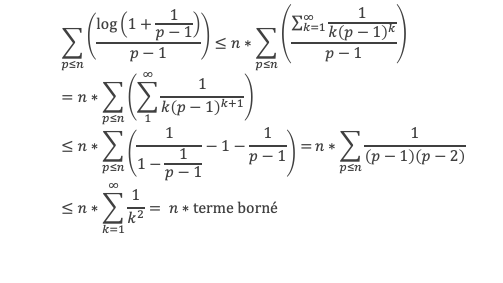
Le second terme est lui aussi de la forme n_*(terme borné).

ll vient :

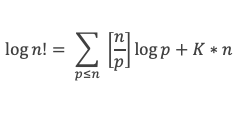
Comme de plus :

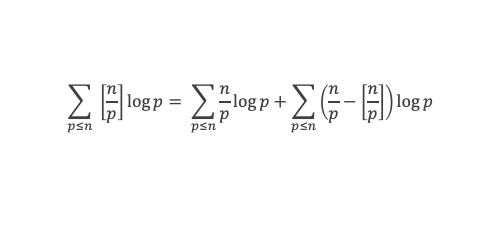
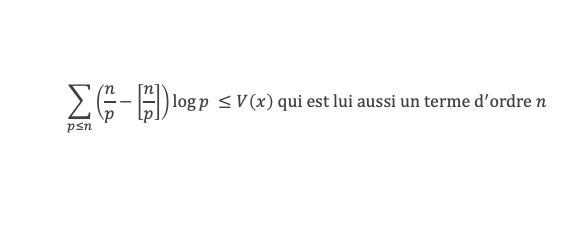
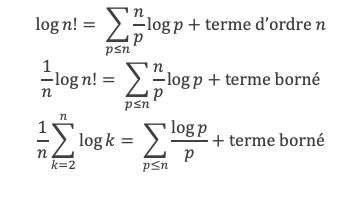
Il reste à calculer la somme des log k, et pour cela exploitons la relation suivante, vraie pour k entier ≥ 2

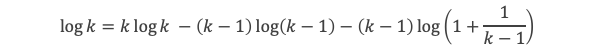
La somme de 2 à n des log k donnera n log n pour la sommation des 2 premiers termes de la relation, plus la sommation de 2 à n du terme (k-1) log ( 1 + 1/(k-1) ) que nous devons maintenant calculer.

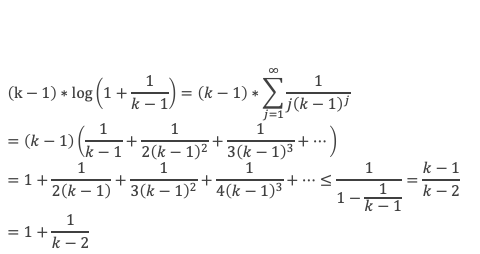
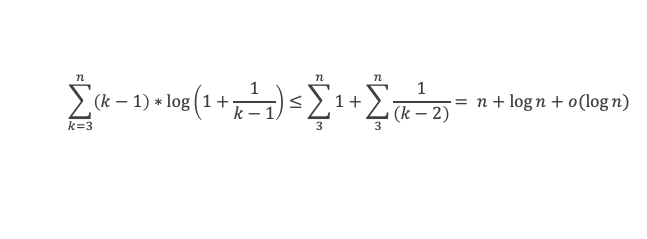
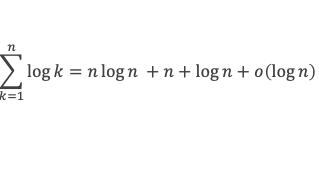
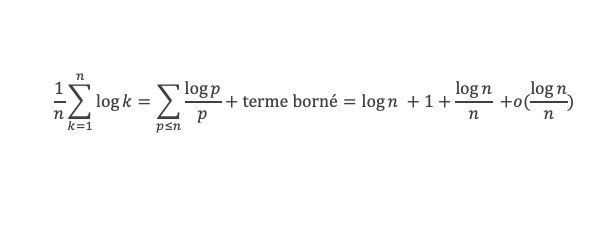
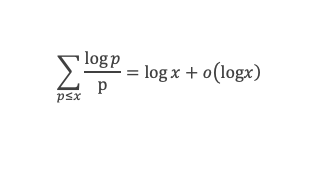
Dans un premier temps nous allons pouvoir montrer que 2 ≥ A + a.

Pour tout δ positif, on sait, par l’étape 2 que pour x suffisamment grand et pour chaque p ≤ √x on a V(x/p) > (a – δ)_*x/p, et donc :

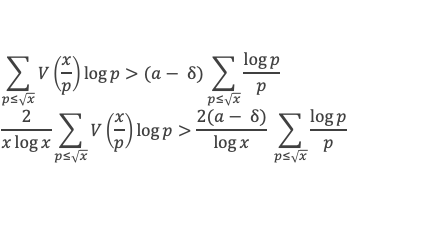
Où nous voyons apparaitre une somme de log p / p, étendue sur les nombres premiers inférieurs à √x. D’après le lemme 13 que nous venons de voir, cette somme est de l’ordre de log (√x) à o(log(x) près, c’est à dire de l’ordre de (log x) / 2, ce qui revient à :

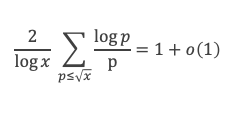
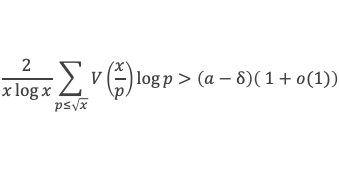
Appliquons ce résultat à la formule de Selberg :

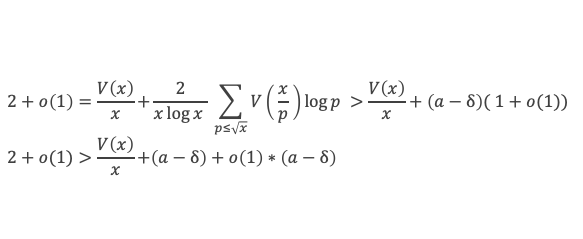
Il est toujours possible de choisir une sous suite de x_i qui tend vers l’infini et telle que V(x_i)/x_i tende vers A. Avec cette suite de x_i on obtient par passage à la limite lorsque les x_i tendent vers l’infini :

2 ≥ A + a – δ

Et comme cela est vrai pour tout δ,

2 ≥ A + a

Recommençons le même raisonnement, mais cette fois avec l’information de l’étape 2 qui nous dit que pour x suffisamment grand et pour p ≤ √x on a V(x/p) < (A + δ)_*x/p, et donc :

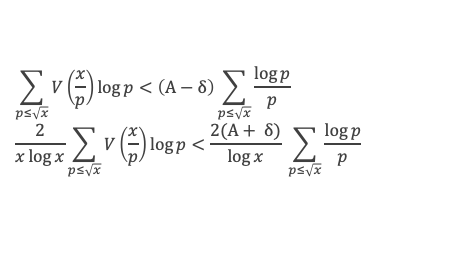
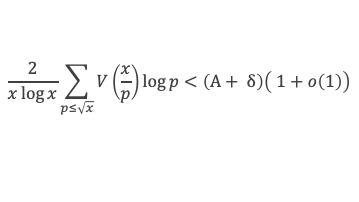
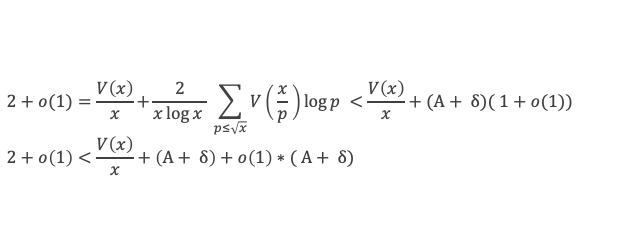
Il est toujours possible de choisir une sous suite de x_j qui tend vers l’infini et telle que V(x_j)/x_j tende vers a. Avec cette série on obtient par passage à la limite lorsque les x_i tendent vers l’infini :

2 ≤ A + a + δ

Et comme cela est vrai pour tout δ,

2 ≤ A + a

Conclusion : nous venons de voir successivement que 2 ≥ A + a et que 2 ≤ A + a. L’égalité 2 = A + a est démontrée. Nous pouvons passer à l’étape 4.

ETAPE 4

Montrons enfin que a = A.

La démonstration repose sur une preuve par l’absurde. Nous allons supposer que a < A, et voir que cela aura pour conséquence a ≥ A ce qui est contraire à l’hypothèse. On en déduira que a ≥ A, et comme par ailleurs nous savons que a ≤ A puisque a est la borne Min et A la borne Max de l’encadrement de V(x)/x, cela permettra de conclure immédiatement que a = A.

Supposons donc que a < A, et considérons σ réel positif, σ > 1 , tel que : σ a < A. On a A – σ a > 0, et donc il existe δ réel positif, suffisamment petit pour que A – σ a ≥ δ(σ + 2) = δσ + 2δ, c’est à dire de façon équivalente : A – δ a ≥  σ a + δσ + δ    (4.1)

Soit N entier quelconque fixé, et l’ensemble E3(N) = ensemble des couples p, q, tels que p ≤ √x; q ≤ √(x/p), pq ≥ N, et qui vérifient en plus V(x/pq) ≥ (A – δ) x/pq .

Soit E4(p, q) = pour p et q de E3(N) donnés, l’ensemble des r tels que (pq) /σ  < r  ≤ σ pq . Cet ensemble n’est pas vide pour p et q suffisamment grands, puisque σ > 1.

Étudions maintenant la somme S(x) définie par :

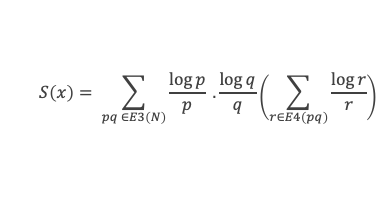
Nous allons montrer que S(x) est un o(log² x), c’est-à-dire que S(x)/log² x tend vers 0 quand x tend vers l’infini.

Tout d’abord, pour chaque r de la somme sur E4(pq) nous avons : r ≤ σ pq = σ √p (√p q) = σ √p √(pq²) et comme p ≤ √x et q ≤ √(x/p) on aura r ≤ σ x^1/4 √x = σ x^3/4 ≤ x à partir d’un certain rang.

De plus, pour x suffisamment grand, chaque r de E4(p, q) vérifie V(x/r) ≥ (a + δ ) x/r . Pour le démontrer nous allons successivement considérer les cas ou r ≤ pq et r > pq.

• Cas où r ≤ pq :

V(x/r) ≥ V(x/pq) par croissance de V, et V(x/pq) ≥ (A – δ) x/(pq) , car p et q appartiennent à E3(N).

Donc V(x/r) ≥ (A – δ) x/(pq) ≥ (A – δ) x/(σr) et en se rappelant que la relation (4.1) donne (A – δ) > σa + δσ + δ  ≥ σ (a + δ) on obtient bien V(x/r) ≥ (a + δ) x/r.

• Cas où r > pq :

On pose u = x/r et v = x/(pq). On a u < v (puisqu’on est dans le cas r > pq ) et v < σ u par définition de E4(p, q). Appliquons la formule de Selberg à respectivement u et v et soustrayons les 2 relations :

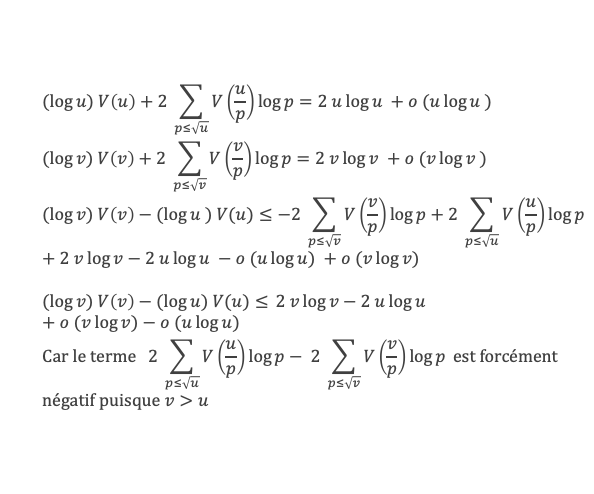
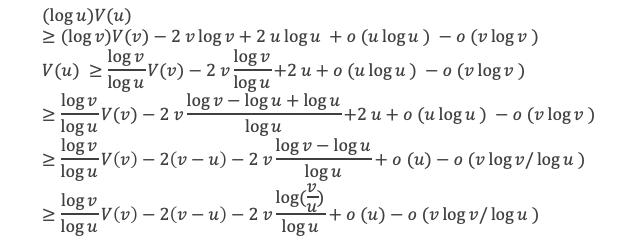
v et u sont du même ordre, à un facteur plus petit que σ ou 1/σ près donc o(v log v / log u) et 2 v log (v/u) / (log u) sont aussi des o(u) car leur rapport avec u tend vers 0 quand u tend vers l’infini. On a donc finalement, sachant que (log v / log u) ≥ 1 et que V(v) ≥ (A – δ)v car v a été défini par v = x/(pq) avec pq dans E3(N) :

V(u) ≥ (A – δ)v – 2(v – u) + o(u) = 2u + (A – δ – 2)v + o(u)

Et sachant que A – 2 = a, cela donne : V(u) ≥  2u – (a + δ)v + o(u), puis en exploitant la relation v < σu : V(u) ≥  2u – (a + δ)σu + o(u), soit : V(u) ≥  ( 2 – (a + δ)σ )u + o(u).

En utilisant maintenant la relation 4.1 qui établit que –σ a – δ a ≥  –A + δσ + δ nous avons –σ a – δ a ≥  –A + 2δ , puisque σ > 1. On en déduit : 2 – (a + δ)σ ≥ 2 – A + 2δ, d’où :

V(u) ≥ (2 – A + 2δ)u + o(u) = (a + 2δ)u + o(u) = (a + δ)u + δu + o(u).

Pour x suffisamment grand u = x/r deviendra suffisamment grand pour garantir (δu + o(u) )> 0 et on aura donc bien V(u) ≥  (a + δ)u, c’est-à-dire finalement :

V(x/r) ≥  (a + δ) x/r

Donc à partir d’un certain rang, que r soit < pq ou r ≥ pq, nous aurons pour chaque r de E4(p, q) : V(x/r) ≥  (a + δ) x/r. De plus nous avons aussi vu auparavant que pour chaque r de E4(p, q) r ≤ x à partir d’un certain rang.

Revenons maintenant à l’évaluation de la somme S(x) dont on cherche a prouver que c’est un o (log² x). Lorsque l’on développe la somme S(x), chaque terme (log r)/r de la somme sur E4(p, q) se retrouve en produit de tous les (log p)/p (log q)/q qui vérifient : p ≤ √x, q ≤ √(x/p) , pq ≥ N, r/σ < pq < σr.

En mettant chaque (log r)/r en facteur de tous les (log p)/p (log q)/q concernés, on obtiendra donc un terme de la forme :

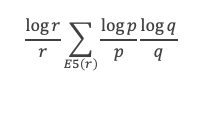
En élargissant la somme sans la limitation sur N on aura :

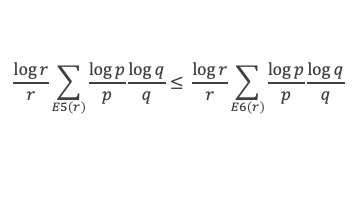
En élargissant encore la sommation de S(x) qui portait initialement sur les r de E4(p, q) à la sommation sur les r qui vérifient r ≤ x et V(x/r) ≥ (a + δ) x/r on écrit finalement, avec E7(x) = ensemble des r tels que  V(x/r) > (a + δ) x/r :

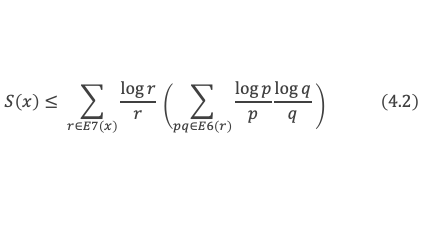
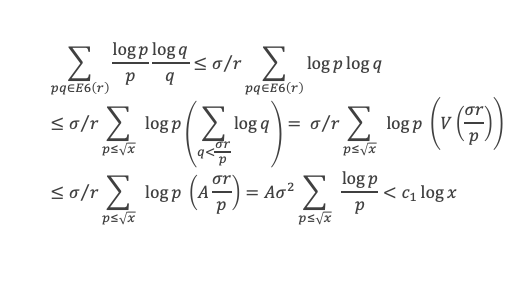
Par conséquent, en utilisant le lemme 14 en annexe qui démontre que la somme des (log r)/r sur r appartenant à E7(x) est un o(log x) on obtient le résultat 4.3 que l’on cherchait :

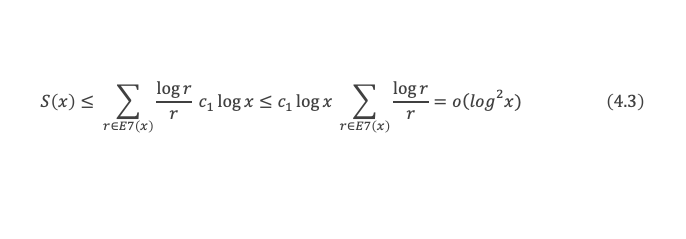
Introduisons maintenant la somme T(x), établie sur l’ensemble E8(p, q) des couples p, q qui vérifient p ≤ √x, q ≤ √(x/p)  et pq ≥ N, . On note que E8(p, q) = E3(p, q) + les couples (p, q) qui vérifient p ≤ √x, q ≤ √(x/p) , pq ≥ N,  et V(x/pq) < (A – δ)x/pq.

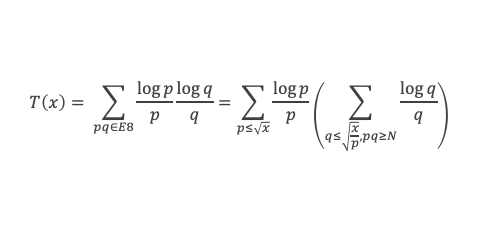
Restreignons la somme à l’ensemble des pq tel que : √N ≤ p ≤ √x, √N ≤ q ≤ x^1/4, et pq ≥ N. Il s’agit bien d’une restriction, évidente pour les p, et pour q on a bien q ≤ x^1/4 ≤ √x/√p car p < √x, et l’on a aussi pq ≥ N, donc :

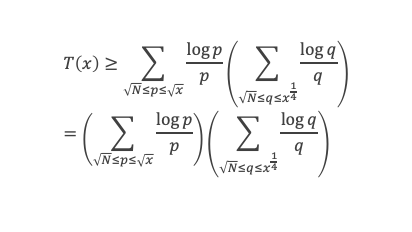
Comme E8(p, q) = E3(p, q) + les (p,q) qui vérifient p ≤ √x, q ≤ √(x/p), pq ≥ N, et V(x/pq) < (A – δ) x/pq , en notant E9(p, q) l’ensemble des (p, q) tels que p ≤ √x, q ≤ √(x/p), pq ≥ N, et V(x/pq) < (A – δ) x/pq , on peut aussi écrire :

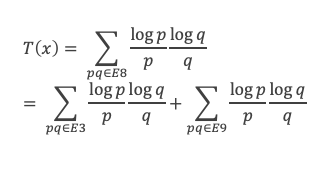
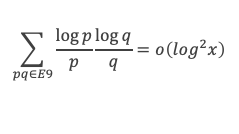
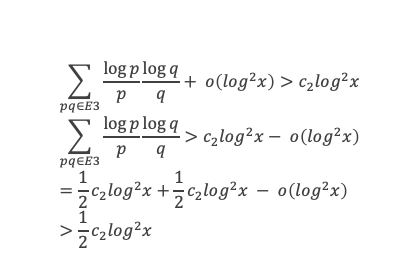
Revenons maintenant à S(x) en se rappelant que :

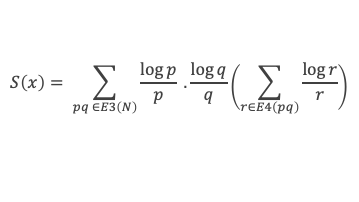
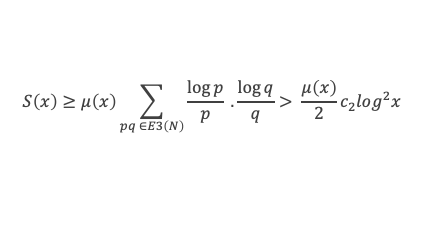
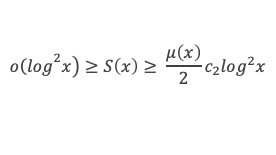
Ce qui implique que forcément la limite de μ(x) = 0 lorsque x tend vers + ∞, avec μ(x) = Min (Σ_E4 log r / r. Par définition, cette valeur Min est obtenue par au moins 1 couple (p, q) de E3 tel que (pq) /σ  < r  < σ pq et tel que :

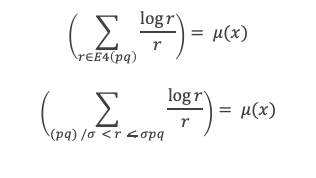
On note t_min la valeur du produit pq de ce couple de E3 qui donne μ(x). On se rappelle que par définition tous les couples (p, q) de E3 vérifient pq ≥ N. Il existe donc t_min ≥ N tel que :

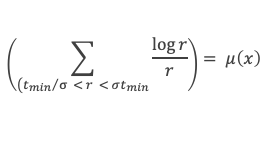
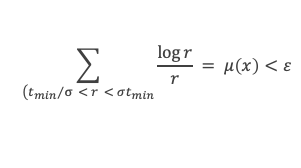
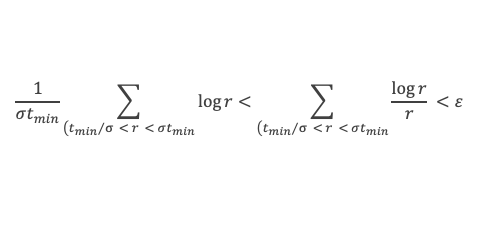
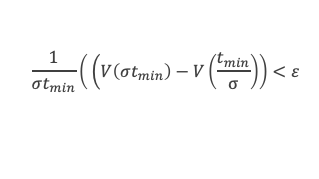
En prenant N suffisamment grand, t_min (qui est supérieur à N) sera suffisamment grand pour que V(σt_min) > (a – ε) σ t_min et V(t_min/σ) < (A + ε) t_min /σ compte tenu de l’encadrement obtenu à l’étape 2. D’où, en repartant du résultat du paragraphe précédent, pour tout ε > 0, ε σt_min > (a – ε) σt_min – (A + ε) t_min /σ, ce qui implique par passage à la limite : 0 ≥ a σt_min – A t_min /σ et donc : σ² a ≤ A, c’est-à-dire σ²  ≤ A/a. 

Or rappelons-nous de la définition de σ au début de l’étape 4 : σ réel positif quelconque > 1 et tel que σ a < A c’est-à-dire σ < A/a.

Prenons σ(x) = A/a – e(x) avec e(x) << 1 et que nous allons faire tendre vers 0.

σ²(x) = (A/a)² -2 e(x) A/a + e²(x) < A/a

(A/a)² -2 e(x) A/a + e²(x) < A/a

(A/a)² –A/a < 2 e(x) A/a – e²(x), et en passant à la limite en faisant tendre e(x) vers 0 :

(A/a)² –A/a ≤ 0

A/a ≤ 1

C’est à dire a ≥ A

Rappelons du début de l’étape 4, nous avons supposé que a < A, et cela donne en conséquence a ≥ A ce qui est contraire à l’hypothèse. On en déduit donc que a ≥ A, et comme par ailleurs nous savons que a ≤ A puisque a est la borne Min et A la borne Max de l’encadrement de V(x)/x cela permettra de conclure immédiatement que a = A.

CQFD

Annexes

Lemme 14 :

Pour λ > a, on considère l’ensemble Eλ(x) défini par Eλ(x) = ensemble des p ≤ x tels que V(x/p) ≥ λ x/p. Le lemme 14 démontre que :

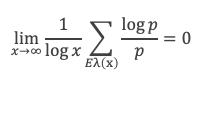
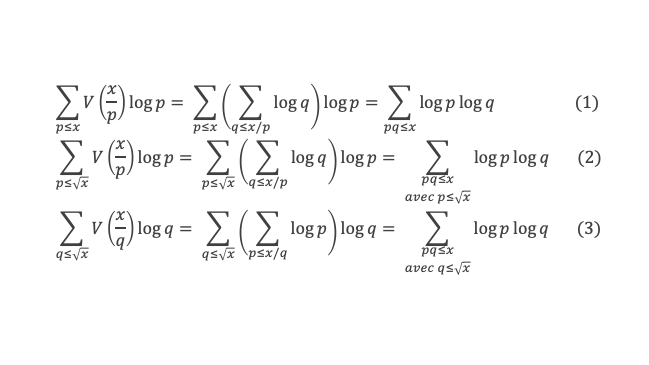
L’ensemble {pq ≤ x} = l’ensemble {pq ≤ x avec p ≤ √x et √x < q ≤ x} U {pq ≤ x avec q ≤ √x et √x < p ≤ x} U {pq ≤ x avec p ≤ √x et q ≤ √x}, donc (1) s’écrit :

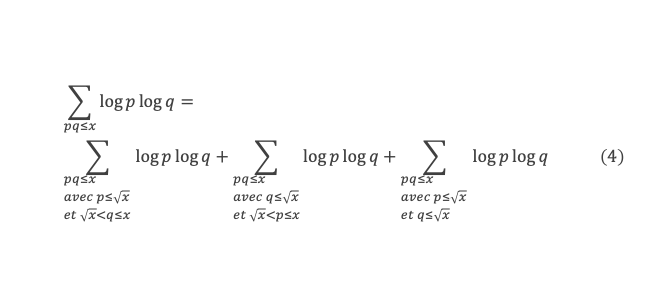
L’ensemble {pq ≤ x avec p ≤ √x} = {pq ≤ x avec p ≤ √x et q ≤ √x} U {pq ≤ x avec p ≤ √x et √x < q ≤ x}, donc (2) s’écrit :

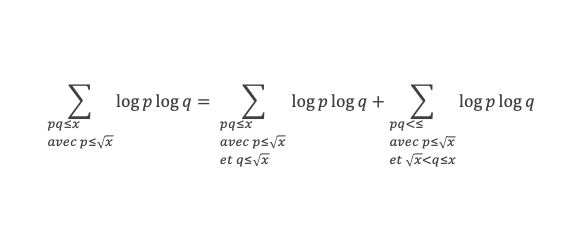
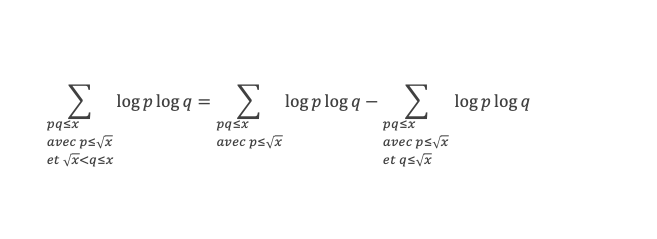
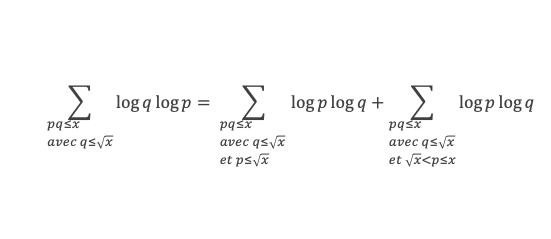
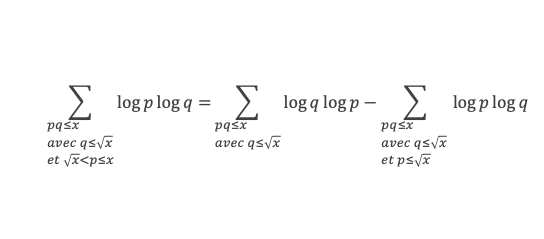
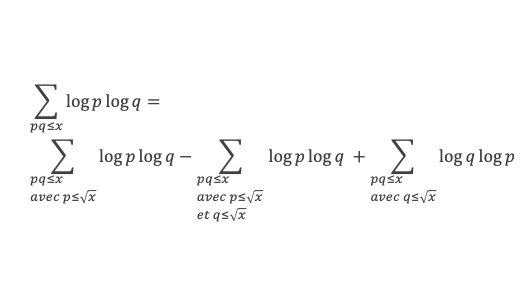
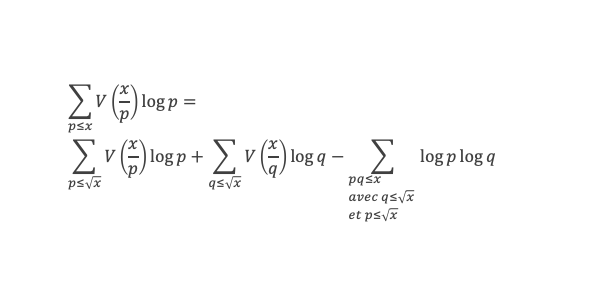
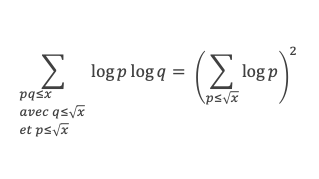
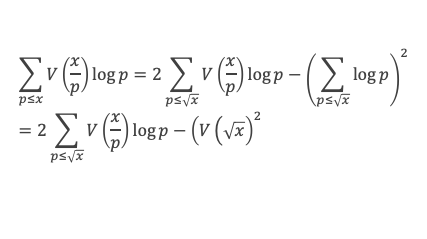
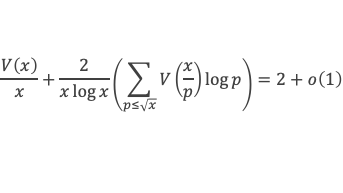
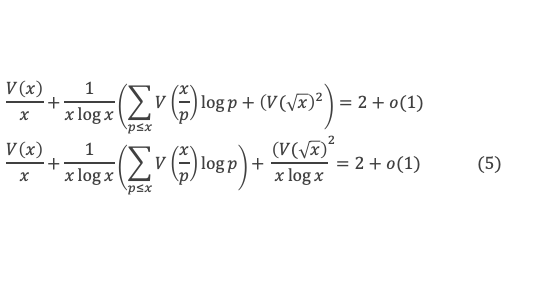
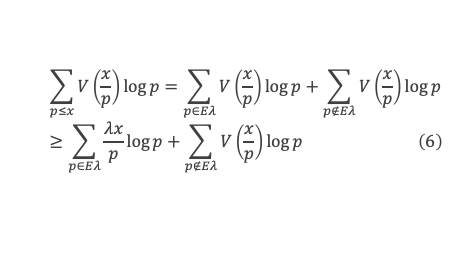
Pour x/p suffisamment grand, disons x/p > u (avec u dépendant de δ), on a V(x/p) > (a  – δ) x/p. En revanche pour x/p ≤ u on aura V(x/p) < (a  – δ) x/p, mais il existe b ≥ 0 tel que pour x/p ≤ u on ait V(x/p) > (a  – δ) x/p – b. Donc :

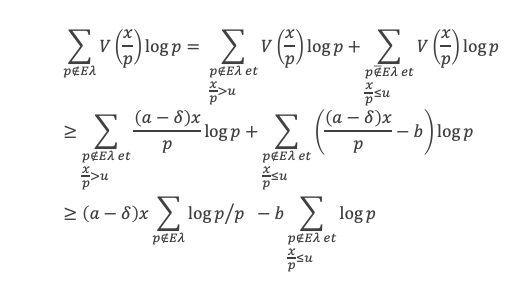
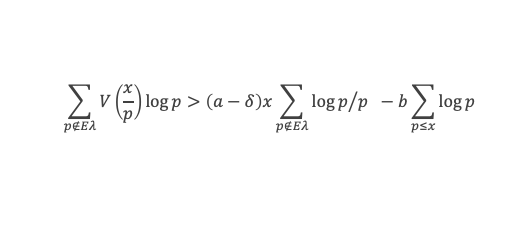
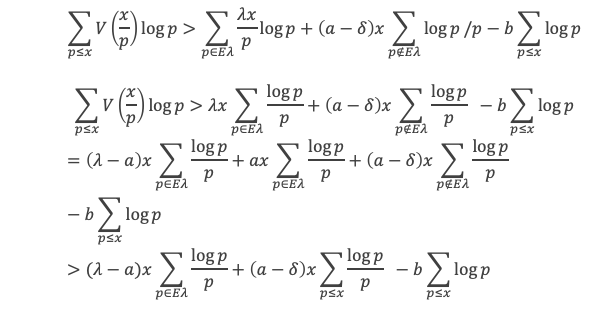
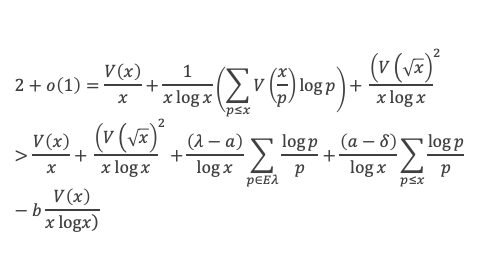
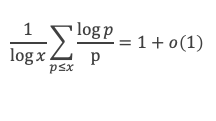
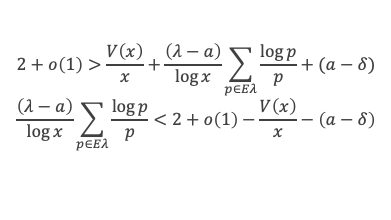
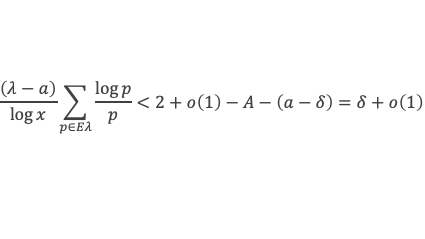
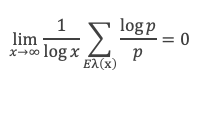
Lemme 15 :

Pour μ < a on considère l’ensemble Eμ(x) défini par Eμ(x) = ensemble des couples p, q, tels que p ≤ √x, q ≤ √(x/p) et qui vérifient en plus V(x/pq) ≤ μ x/pq

Le lemme 15 démontre que :

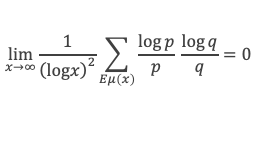
Appliquons une première fois la formule de Selberg en remplaçant x par x/p :